
2
.doc
Практичне заняття № 2. Лінійна залежність та незалежність векторів. Базис. Координати вектора.
Основні теоретичні факти.
Нехай задані вектори
![]() та числа
та числа
![]() .
Вектор
.
Вектор
![]() називається лінійною комбінацією
векторів
називається лінійною комбінацією
векторів
![]() .
Також кажуть, що вектор
.
Також кажуть, що вектор
![]() лінійно виражається через вектори
лінійно виражається через вектори
![]() .
.
Якщо рівність
![]() можлива при деяких ненульових коефіцієнтах,
то вектори
можлива при деяких ненульових коефіцієнтах,
то вектори
![]() називають лінійно залежними.
Якщо ж дана рівність виконується тільки
при нульових коефіцієнтах, то вектори
називають лінійно залежними.
Якщо ж дана рівність виконується тільки
при нульових коефіцієнтах, то вектори
![]() називають лінійно незалежними.
називають лінійно незалежними.
Вектори
![]() лінійно залежні тоді і тільки тоді, коли
один із них є лінійною комбінацією
інших.
лінійно залежні тоді і тільки тоді, коли
один із них є лінійною комбінацією
інших.
Якщо серед векторів
![]() є нульовий вектор, то ці вектори лінійно
залежні.
є нульовий вектор, то ці вектори лінійно
залежні.
Якщо деяка система векторів містить лінійно залежну підсистему, то ці вектори лінійно залежні.
Два вектори лінійно залежні тоді і тільки тоді, коли вони колінеарні.
Три вектори лінійно залежні тоді і тільки тоді, коли вони компланарні.
Будь-які чотири геометричні вектори лінійно залежні.
Упорядковану множину векторів
![]() називають базисом множини
векторів
називають базисом множини
векторів
![]() ,
якщо дані вектори лінійно незалежні, а
також будь-який вектор множини
,
якщо дані вектори лінійно незалежні, а
також будь-який вектор множини
![]() лінійно виражається через вектори
множини
лінійно виражається через вектори
множини
![]() .
.
У просторі компланарних векторів
![]() з деяким базисом
з деяким базисом
![]() довільний вектор
довільний вектор
![]() можна єдиним способом представити у
вигляді
можна єдиним способом представити у
вигляді
![]() .
Коефіцієнти
.
Коефіцієнти
![]() біля базисних векторів називають
координатами вектора
біля базисних векторів називають
координатами вектора
![]() відносно базису
відносно базису
![]() .
Записують
.
Записують
![]() або
або
![]() .
.
У випадку векторного простору не
компланарних векторів
![]() та деякого його базису
та деякого його базису
![]() для довільного вектора
для довільного вектора
![]() його координати аналогічно визначаються,
як коефіцієнти
його координати аналогічно визначаються,
як коефіцієнти
![]() біля базисних векторів у рівності
біля базисних векторів у рівності
![]() .
Записують
.
Записують
![]() або
або
![]() .
.
Два вектори, задані своїми координатами, рівні тоді і тільки тоді, коли їхні відповідні координати рівні.
Додавання та віднімання векторів, а
також множення векторів на числа
здійснюється виконанням відповідних
операцій над координатами векторів.
Тобто, для довільних векторів
![]() та
та
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() - деякий числовий множник.
- деякий числовий множник.
Два вектори, задані своїми координатами, колінеарні тоді і тільки тоді, коли їхні координати пропорційні.
Базис
![]() називають прямокутним декартовим
або ортонормованим, якщо вектори
базису одиничні та взаємно перпендикулярні.
Щоб відрізняти ортонормовані базиси
від інших використовують позначення
базисних векторів у виді
називають прямокутним декартовим
або ортонормованим, якщо вектори
базису одиничні та взаємно перпендикулярні.
Щоб відрізняти ортонормовані базиси
від інших використовують позначення
базисних векторів у виді
![]() .
Отже, базис
.
Отже, базис
![]() - прямокутний декартовий, якщо
- прямокутний декартовий, якщо
![]() та
та
![]() .
У просторі
.
У просторі
![]() ортонормованим буде базис
ортонормованим буде базис
![]() .
.
Довжину вектора
![]() в ортонормованому базисі
в ортонормованому базисі
![]() можна обчислювати за допомогою
співвідношення
можна обчислювати за допомогою
співвідношення
![]() .
Довжина вектора
.
Довжина вектора
![]() в ортонормованому базисі обчислюється
за формулою
в ортонормованому базисі обчислюється
за формулою
![]() .
.
Приклади розв’язання задач.
Задача 1. Задано вектори
![]() ,
,
![]() ,
,
![]() .
Довести, що вони утворюють базис.
Розкласти вектор
.
Довести, що вони утворюють базис.
Розкласти вектор
![]() за даним базисом.
за даним базисом.
Розв’язання. Розглянемо векторну
рівність
![]() .
Прирівнюючи координати векторів у лівій
та правій частині рівності, отримуємо
систему однорідних лінійних рівнянь
.
Прирівнюючи координати векторів у лівій
та правій частині рівності, отримуємо
систему однорідних лінійних рівнянь
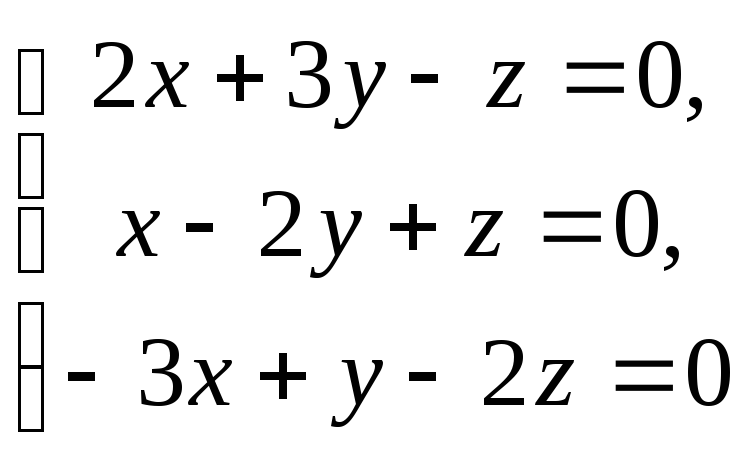 ,
визначник якої
,
визначник якої
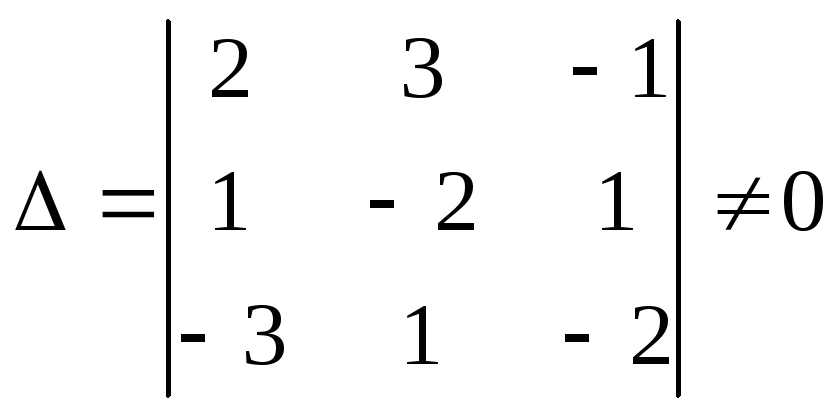 .
Тому система має тільки нульовий
розв’язок. Отже, дані вектори лінійно
незалежні і утворюють базис.
.
Тому система має тільки нульовий
розв’язок. Отже, дані вектори лінійно
незалежні і утворюють базис.
Із векторної рівності
![]() дістаємо систему координатних рівностей
дістаємо систему координатних рівностей
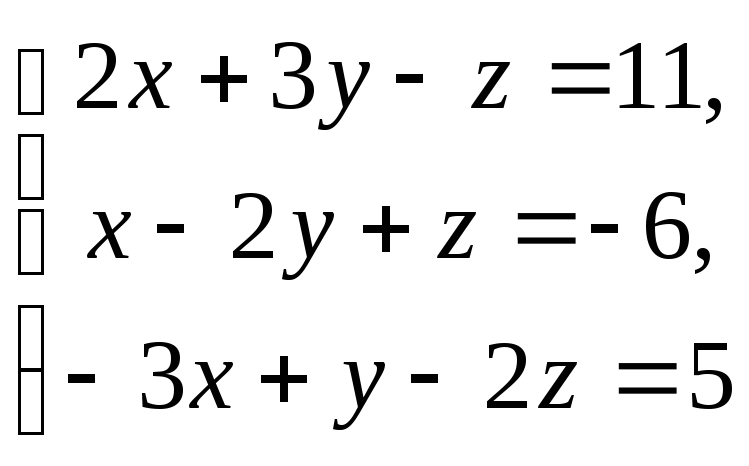 , розв’язуючи яку, знаходимо
, розв’язуючи яку, знаходимо
![]() .
.
Таким чином,
![]() .
.
Задача 2. Знайти лінійну
залежність між векторами
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Розв’язання. Нас цікавить хоча
б один ненульовий набір коефіцієнтів
![]() у векторній рівності
у векторній рівності
![]() .
Переходячи до координатних рівностей,
одержуємо систему однорідних лінійних
рівнянь
.
Переходячи до координатних рівностей,
одержуємо систему однорідних лінійних
рівнянь
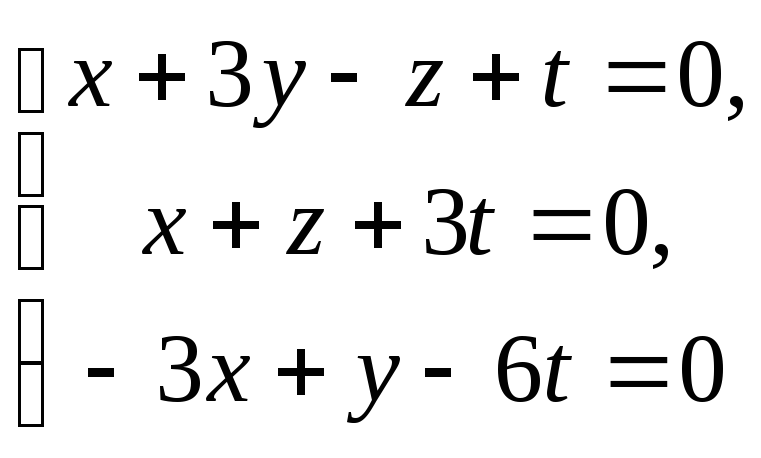 ,
яка, як відомо із курсу лінійної алгебри,
має безліч розв’язків. Одним із них є
розв’язок
,
яка, як відомо із курсу лінійної алгебри,
має безліч розв’язків. Одним із них є
розв’язок
![]() .
Відповідь отримуємо у виді рівності
.
Відповідь отримуємо у виді рівності
![]() .
.
Задача 2. У трикутнику
![]() на сторонах
на сторонах
![]() і
і
![]() вибрано точки
вибрано точки
![]() та
та
![]() так, що
так, що
![]() ,
а також проведено відрізки
,
а також проведено відрізки
![]() і
і
![]() ,
які перетинаються у точці
,
які перетинаються у точці
![]() .
У якому відношенні точка
.
У якому відношенні точка
![]() ділить дані відрізки?
ділить дані відрізки?
Розв’язання. Нехай
![]() ,
,
![]() (рис. 1). Оскільки
(рис. 1). Оскільки
![]() ,
то
,
то
![]() .
Виразимо всі вектори в одержаній
векторній рівності через
.
Виразимо всі вектори в одержаній
векторній рівності через
![]() та
та
![]() .
.
![]() ,
,
![]() .
.
Отже,
![]() .
.
Оскільки вектори
![]() та
та
![]() лінійно незалежні, то, прирівнюючи
коефіцієнти біля цих векторів в обох
частинах рівності, дістаємо систему
рівнянь
лінійно незалежні, то, прирівнюючи
коефіцієнти біля цих векторів в обох
частинах рівності, дістаємо систему
рівнянь
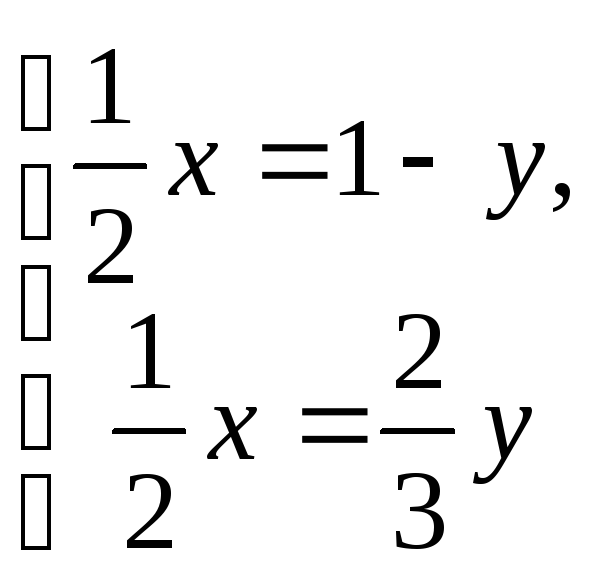
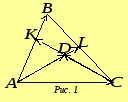 ,
,
розв’язуючи яку, знаходимо
![]() .
Отже,
.
Отже,
![]() .
.
Відповідь.
![]() .
.
З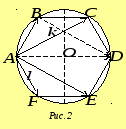 адача
3. Задано правильний шестикутник
адача
3. Задано правильний шестикутник
![]() .
Нехай
.
Нехай![]() .
Знайти координати векторів
.
Знайти координати векторів
![]() та
та
![]() у базисі
у базисі
![]() .
.
Розв’язання. Нехай
![]() - центр кола, описаного навколо заданого
шестикутника (рис. 2). Очевидно, що
- центр кола, описаного навколо заданого
шестикутника (рис. 2). Очевидно, що
![]() ,
,
а також, що
![]() .
Тому
.
Тому
![]()
![]() ,
,
![]() .
.
Відповідь.
![]() .
.
Задача 4. Довести, що відрізки, які сполучають вершини трикутної піраміди з центрами протилежних граней, перетинаються в одній точці та діляться нею у відношенні 3:1, рахуючи від вершини.
Розв’язання . Нехай
![]() - задана піраміда і
- задана піраміда і
![]() ,
точки
,
точки
![]() та
та
![]() - точки перетину медіан відповідно
трикутників
- точки перетину медіан відповідно
трикутників
![]() і
і
![]() ,
точки
,
точки
![]() належать відрізкам
належать відрізкам
![]() та
та
![]() ,
причому
,
причому
![]() .
Покажемо, що у базисі
.
Покажемо, що у базисі
![]() координати векторів
координати векторів
![]() та
та
![]() співпадають. Маємо
співпадають. Маємо
![]()
![]()
![]() ,
,
де
![]() - середина відрізка
- середина відрізка
![]() .
Отже, у базисі
.
Отже, у базисі
![]() вектор
вектор
![]() має координати
має координати
![]() .
Дальше знаходимо
.
Дальше знаходимо
![]()
![]() ,
,
тобто
![]() .
Таким чином,
.
Таким чином,
![]() ,
а це означає, що точки
,
а це означає, що точки
![]() та
та
![]() співпадають.
співпадають.
Задача 5. У трапеції
![]() з основами
з основами
![]() відомо, що
відомо, що
![]() .
Обчислити координати вектора
.
Обчислити координати вектора
![]() у базисі
у базисі
![]() ,
якщо
,
якщо
![]() - точка перетину діагоналей трапеції,
- точка перетину діагоналей трапеції,
![]() (рис. 3).
(рис. 3).
Розв’язання. Із трикутника
![]() знаходимо
знаходимо
![]() .
.
Оскільки трикутники
![]() та
та
![]() подібні, то
подібні, то
![]() ,
,
з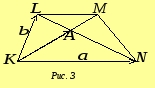 відки
відки
![]() .
Тому
.
Тому
![]()
![]() .
.
Коефіцієнти біля векторів
![]() та
та
![]() дозволяють отримати відповідь:
дозволяють отримати відповідь:
![]() .
.
Задачі для самостійного розв’язання.
-
Вектори
 та
та
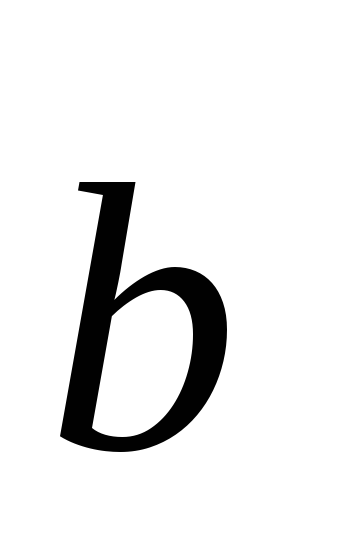 лінійно незалежні. Визначити, при якому
значенні параметра
лінійно незалежні. Визначити, при якому
значенні параметра
 будуть лінійно залежними вектори
будуть лінійно залежними вектори
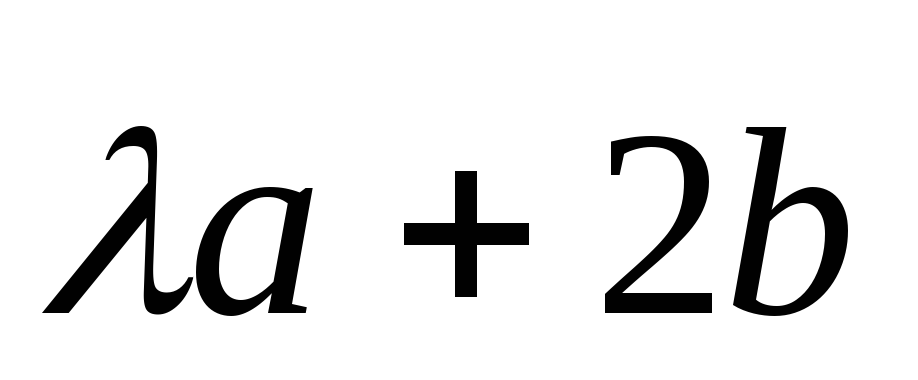 та
та
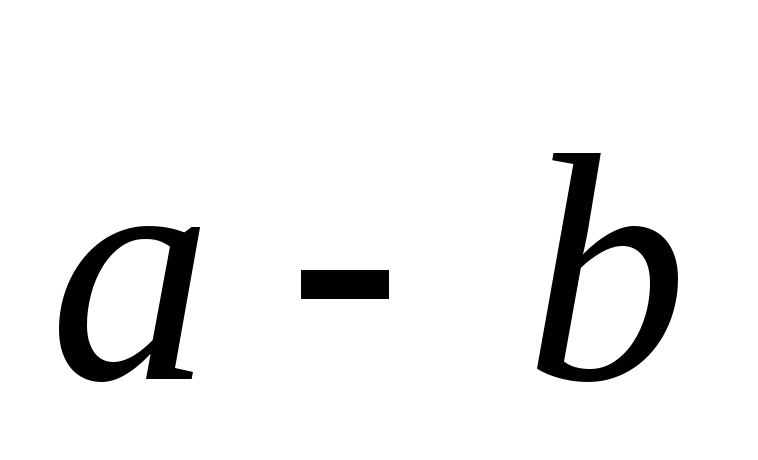 ?
?
![]() .
.
-
Довести, що для будь-яких векторів
 вектори
вектори
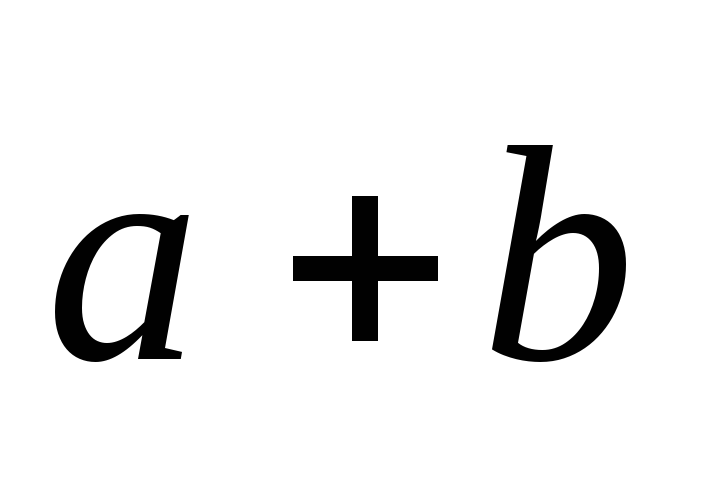 ,
,
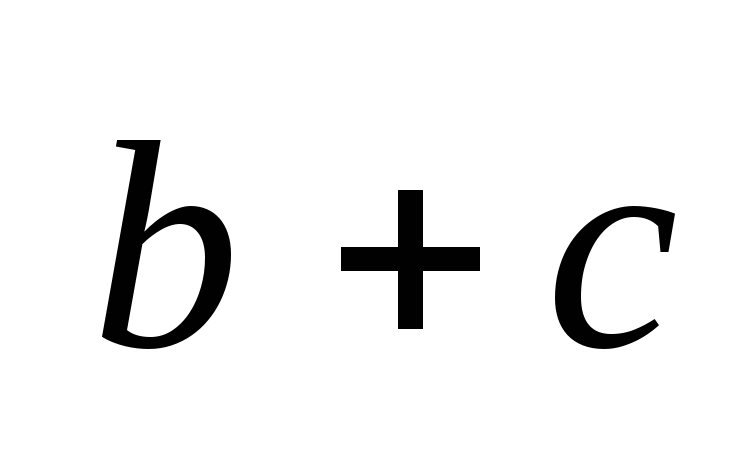 та
та
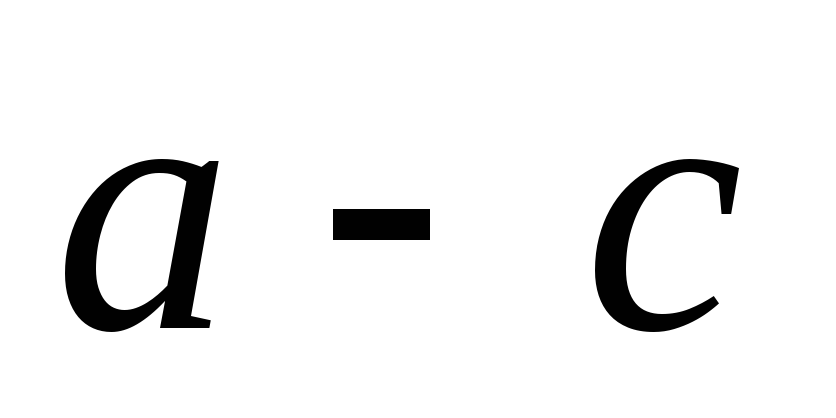 лінійно залежні.
лінійно залежні. -
У трикутнику
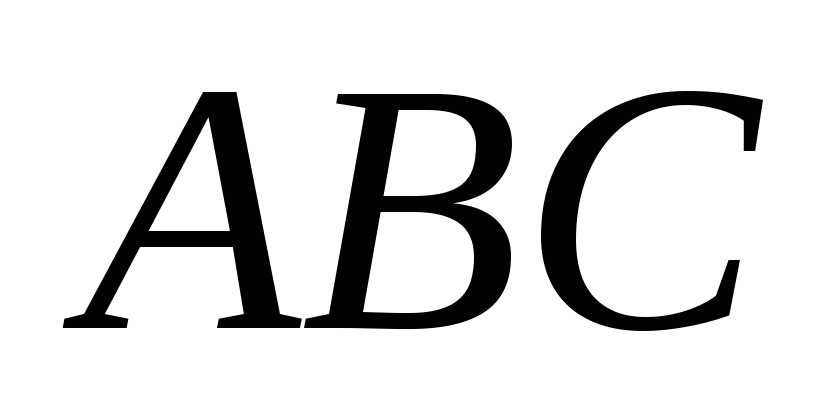 на сторонах
на сторонах
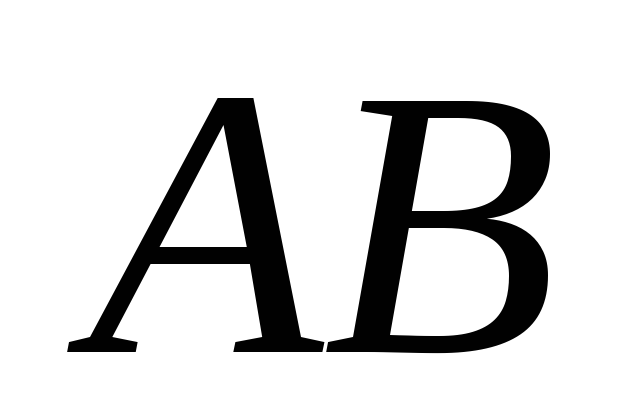 і
і
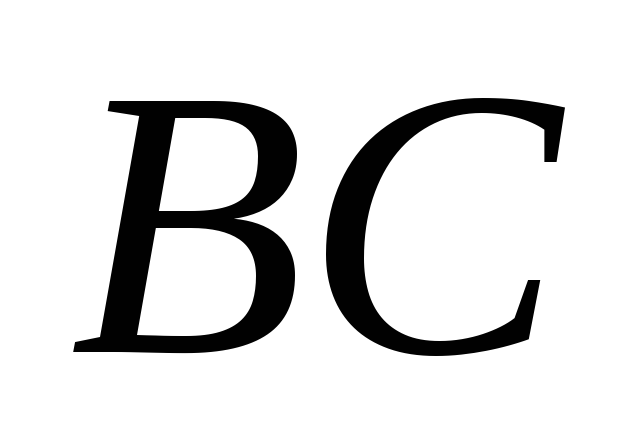 вибрано точки
вибрано точки
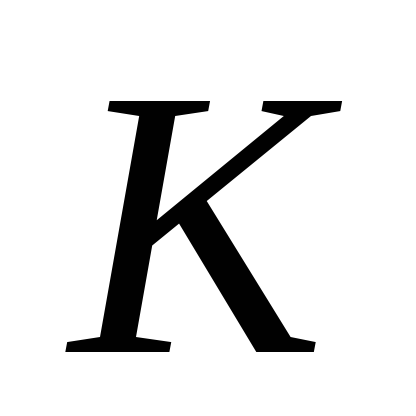 та
та
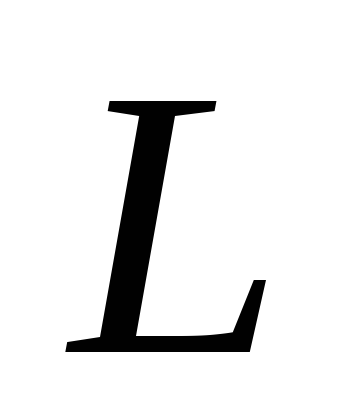 так, що
так, що
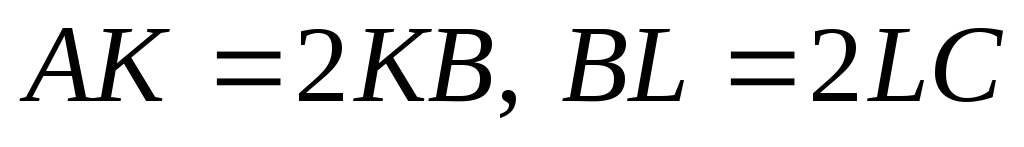 ,
а також проведено відрізки
,
а також проведено відрізки
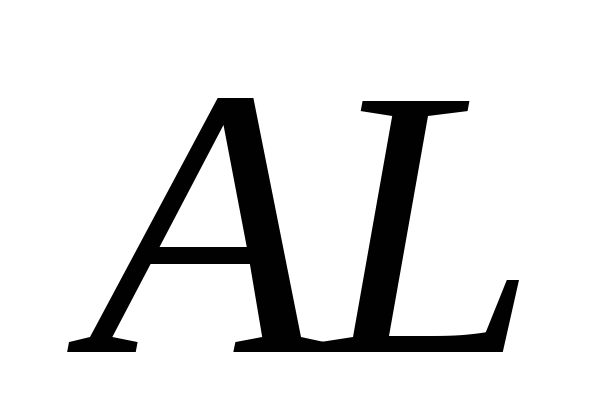 і
і
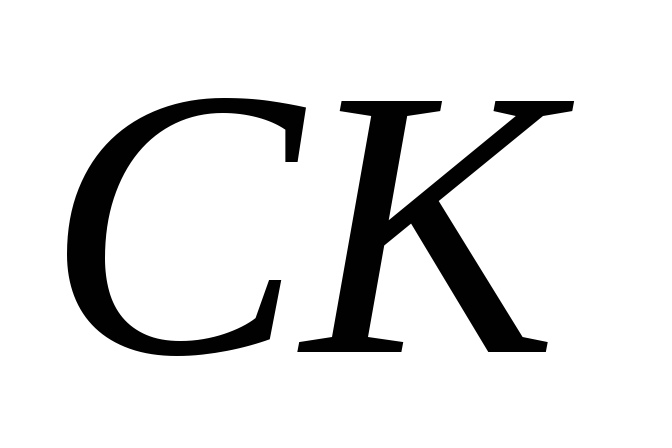 ,
які перетинаються у точці
,
які перетинаються у точці
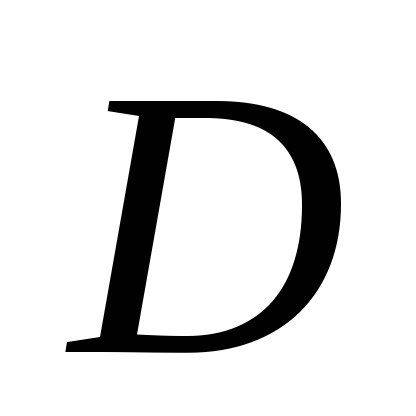 .
У якому відношенні точка
.
У якому відношенні точка
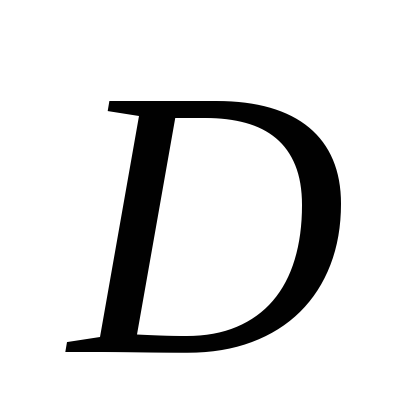 ділить дані відрізки?
ділить дані відрізки? -
У трикутнику
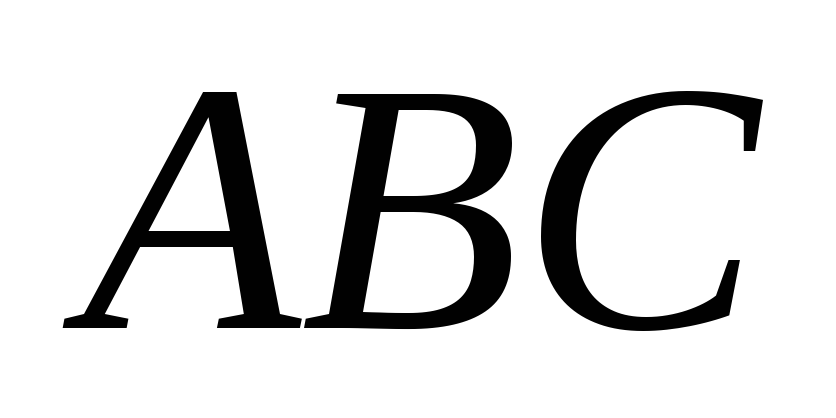 вектори
вектори
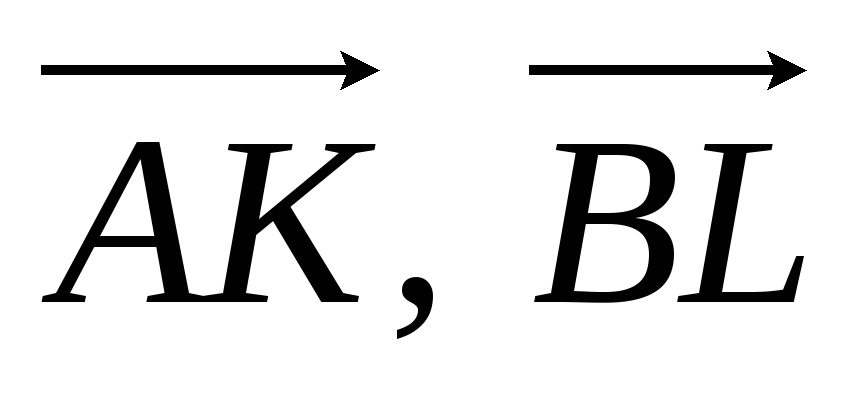 та
та
 напрямлені по медіанах. Виразити їх
через вектори
напрямлені по медіанах. Виразити їх
через вектори
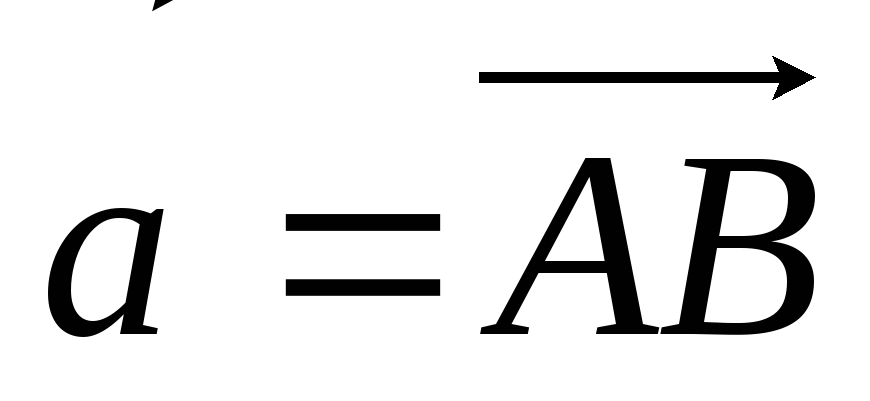 і
і
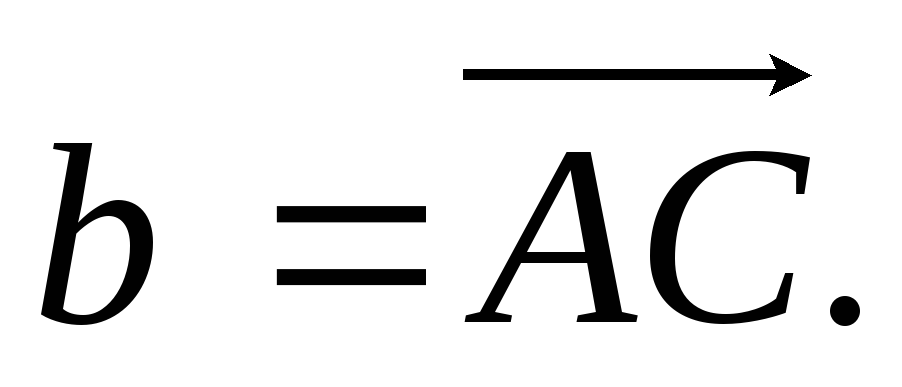
-
Нехай
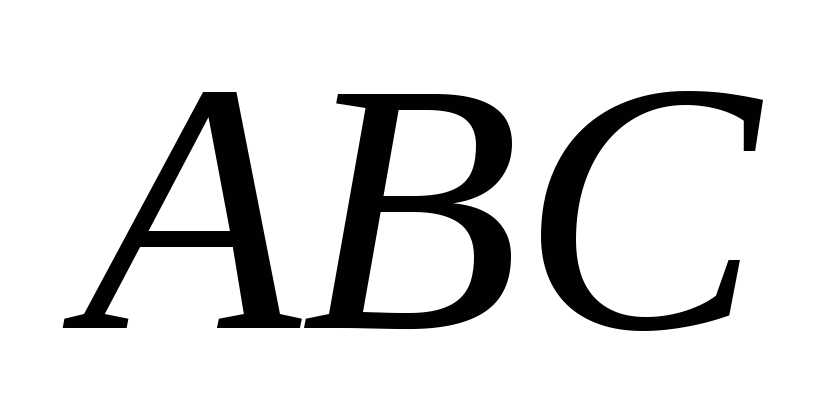 - довільний трикутник,
- довільний трикутник,
 і
і
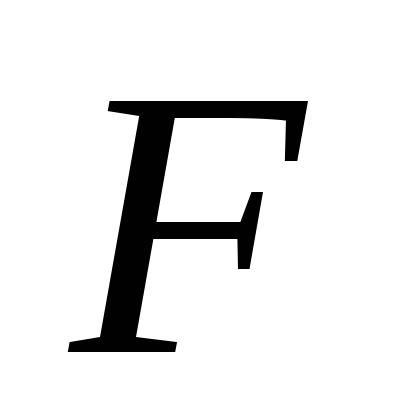 - середини сторін
- середини сторін
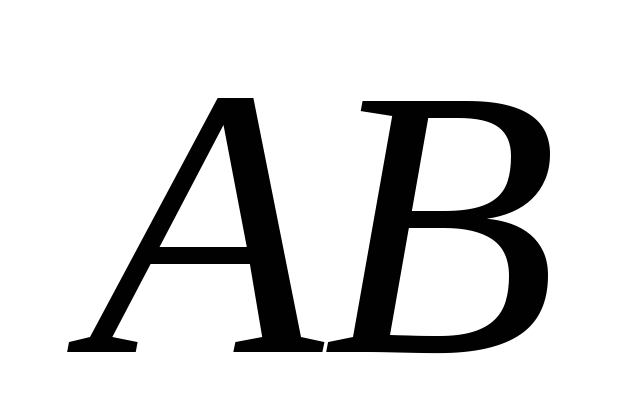 та
та
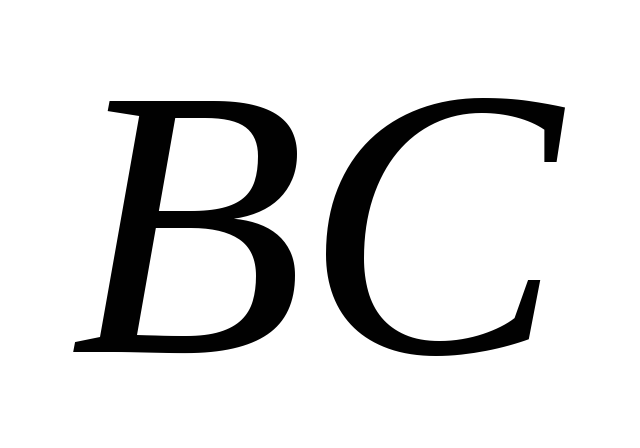 .
Виразити вектори
.
Виразити вектори
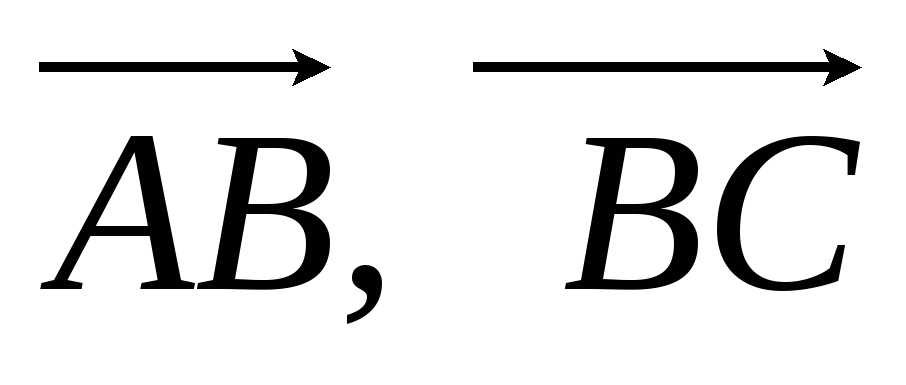 ,
,
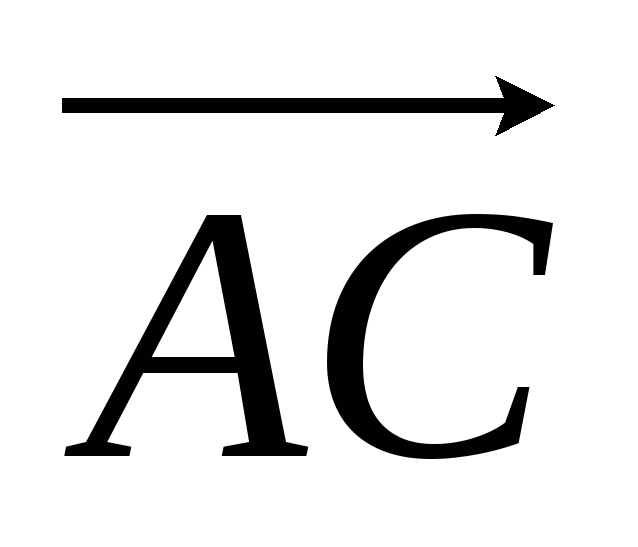 через
через
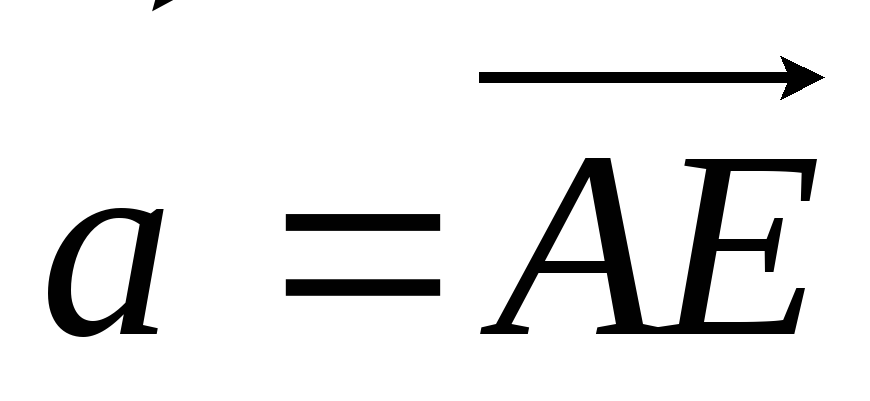 і
і
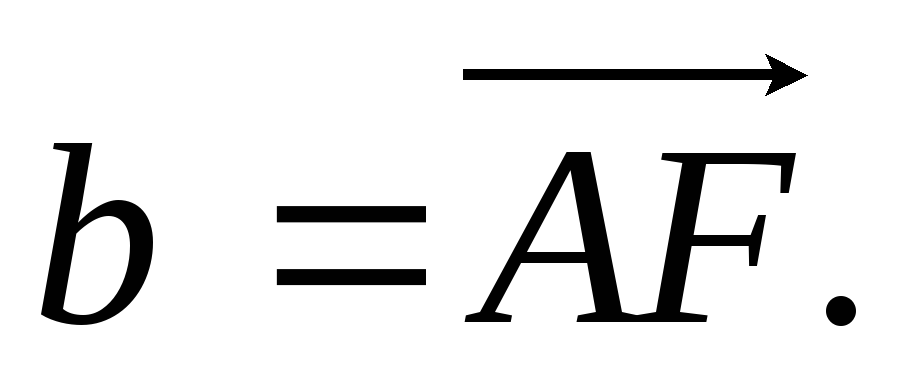
-
Нехай
 - правильний шестикутник, точка
- правильний шестикутник, точка
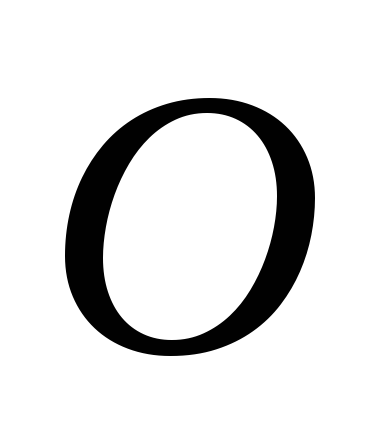 -
його центр. Покладемо
-
його центр. Покладемо
 та
та
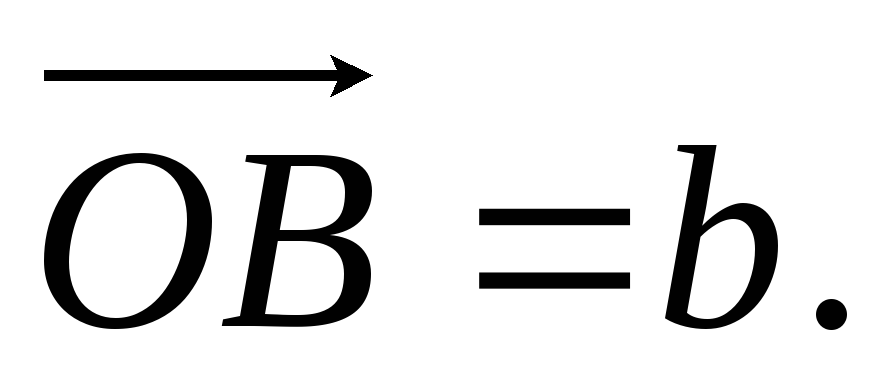 Виразити вектори
Виразити вектори
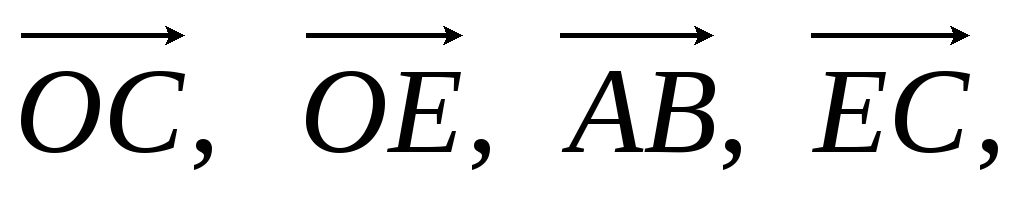
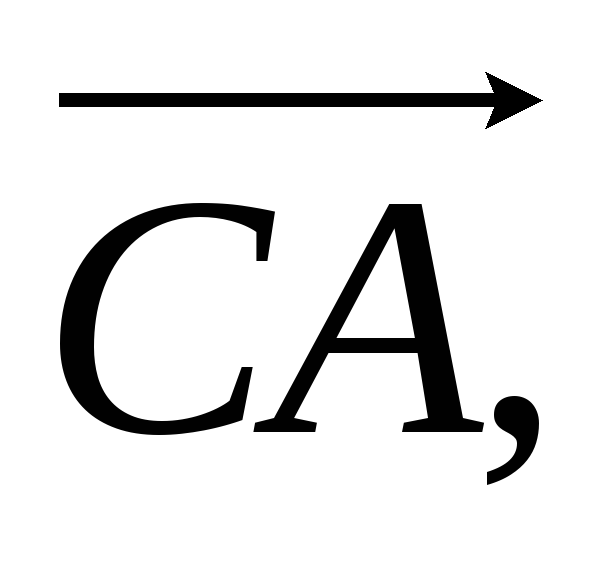
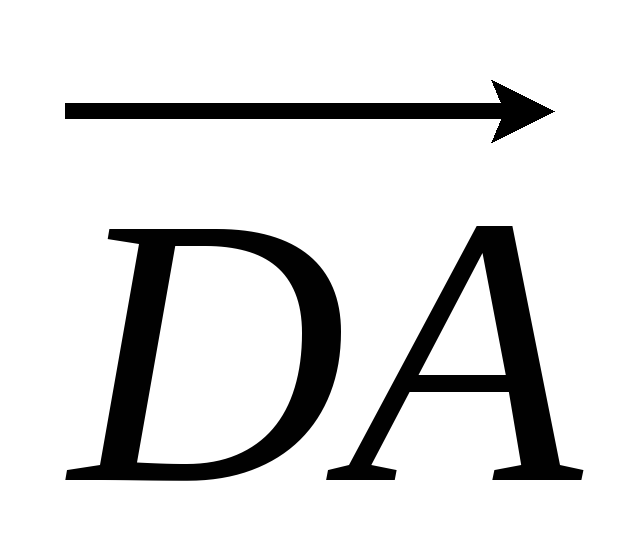 через вектори
через вектори
 та
та
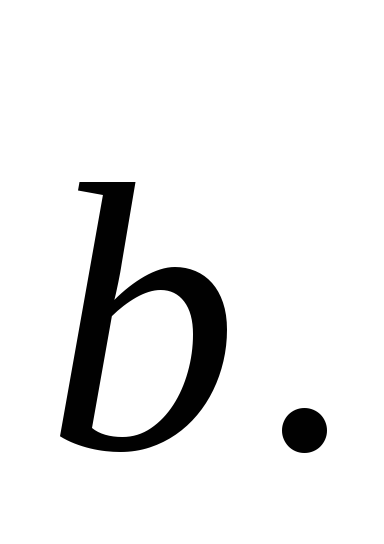
-
У паралелограмі
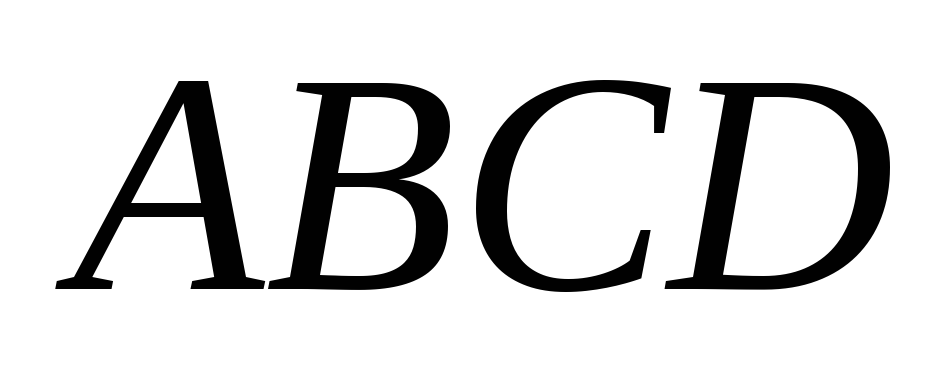 на стороні
на стороні
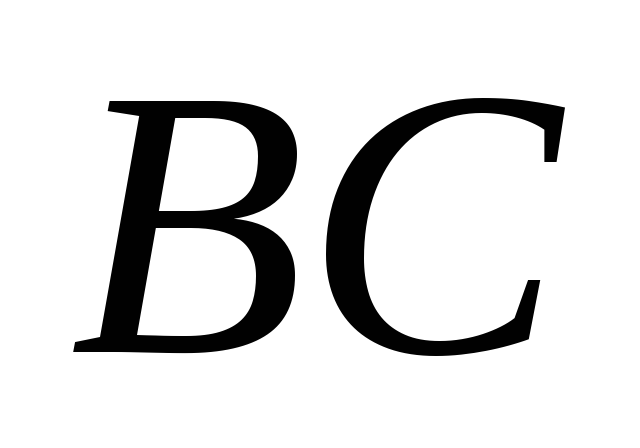 вибрана точка
вибрана точка
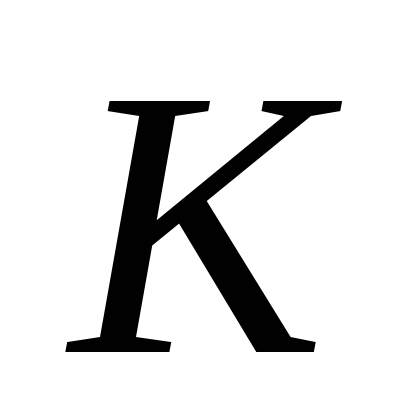 така, що
така, що
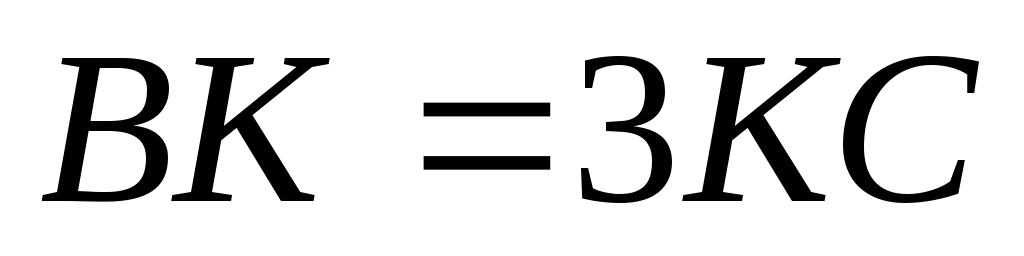 .
У якому відношенні ділить діагональ
.
У якому відношенні ділить діагональ
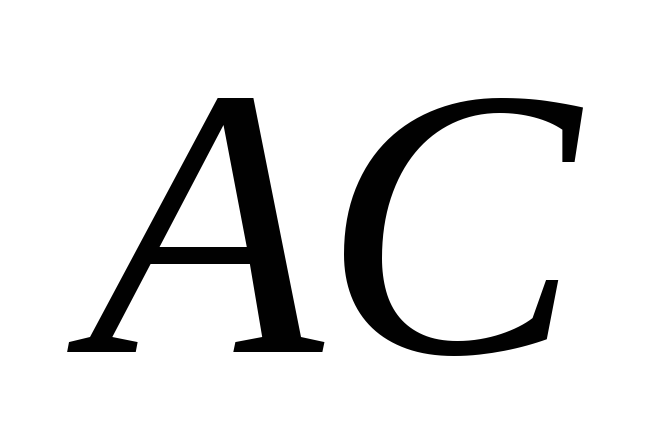 точка її перетину з відрізком
точка її перетину з відрізком
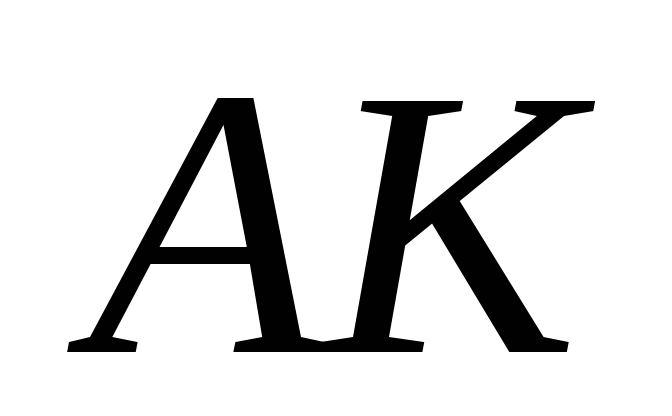 ?
? -
У паралелограмі
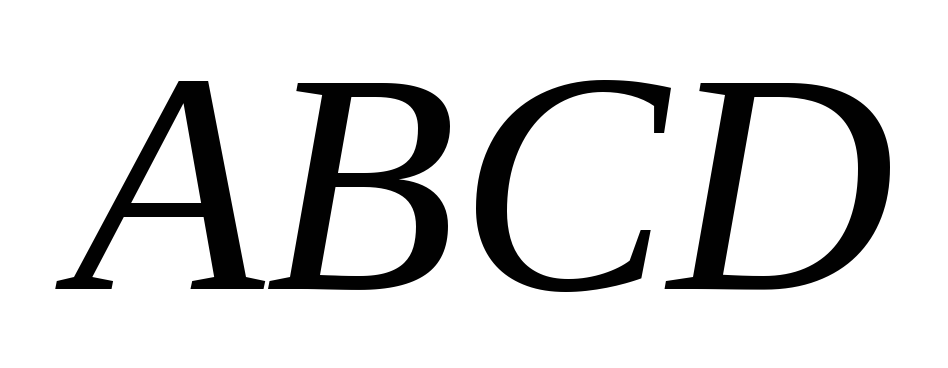 на діагоналі
на діагоналі
 вибрана точка
вибрана точка
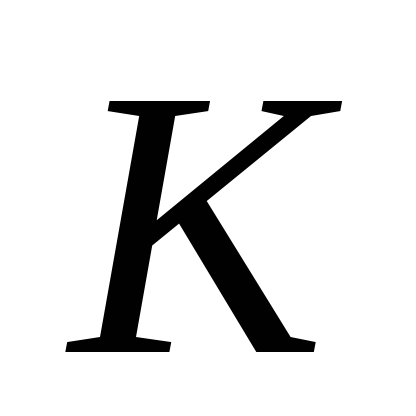 така, що
така, що
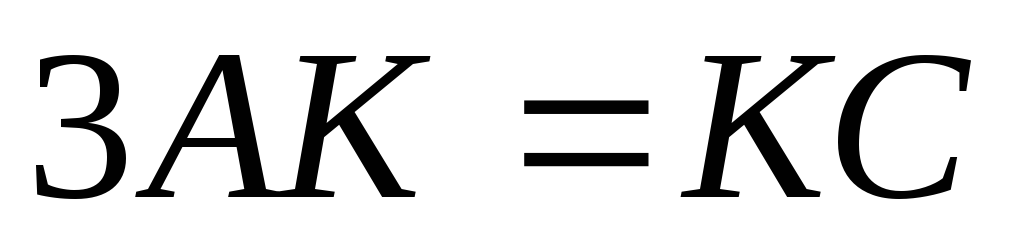 .
У якому відношенні ділить сторону
.
У якому відношенні ділить сторону
 точка
її перетину з прямою
точка
її перетину з прямою
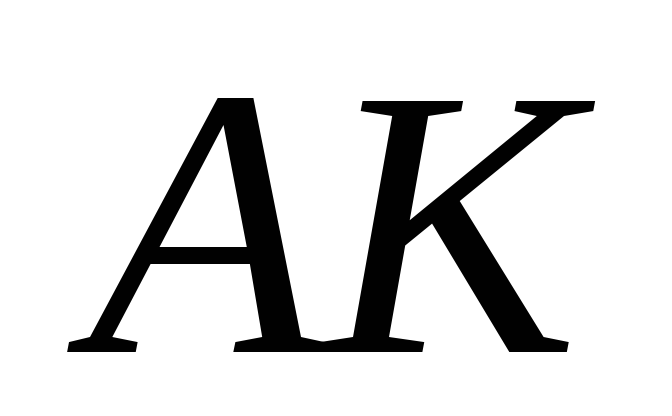 ?
? -
У
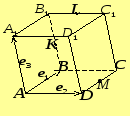 паралелепіпеді
паралелепіпеді
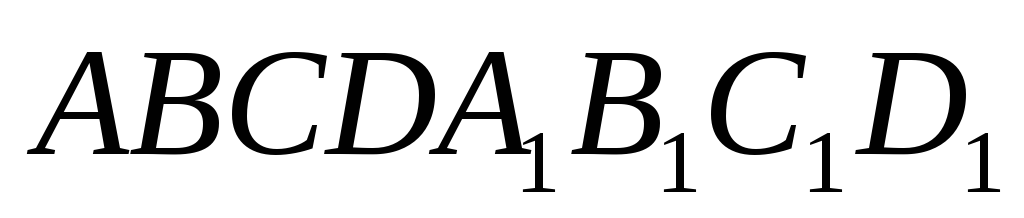 точки
точки
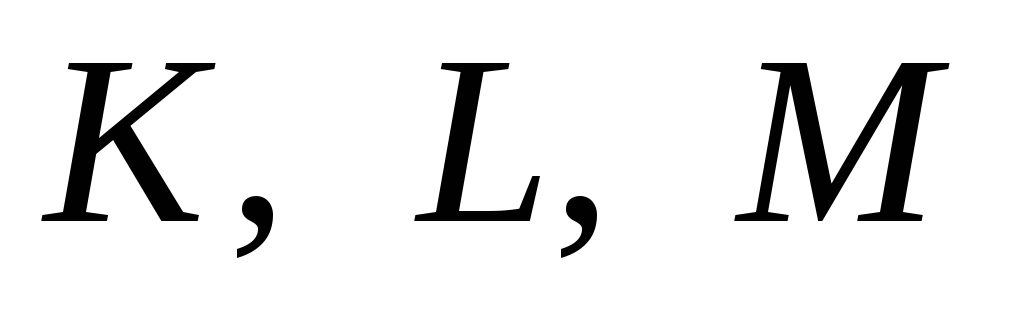 - середини ребер
- середини ребер
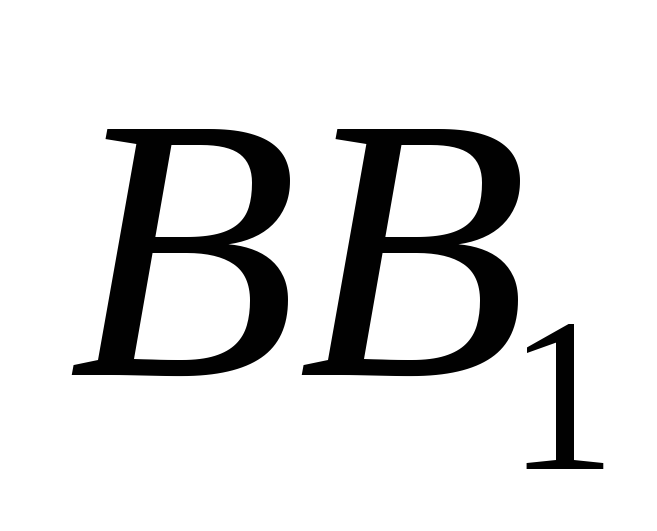 ,
,
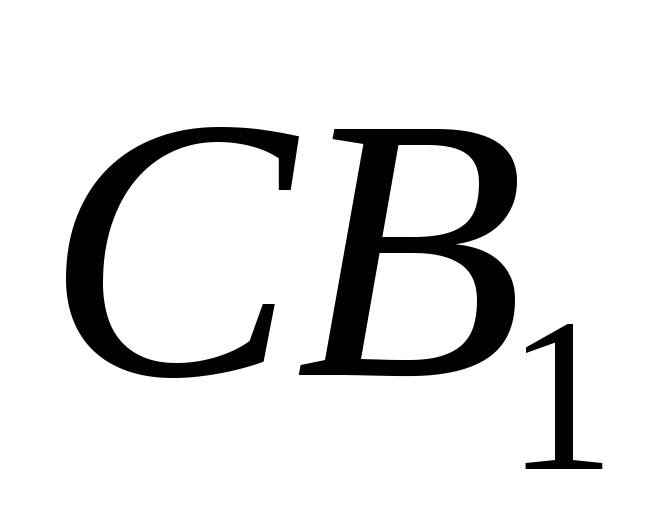 та
та
 відповідно (рис.4). Виразити вектори
відповідно (рис.4). Виразити вектори
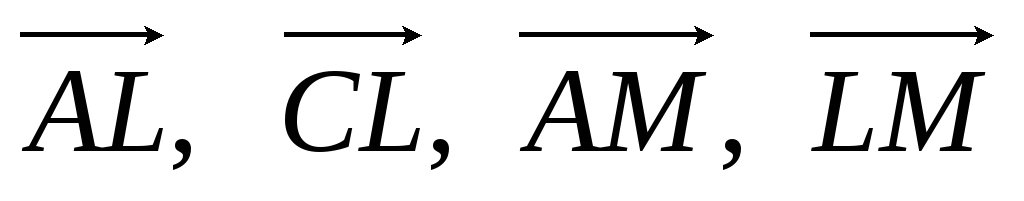 через вектори
через вектори
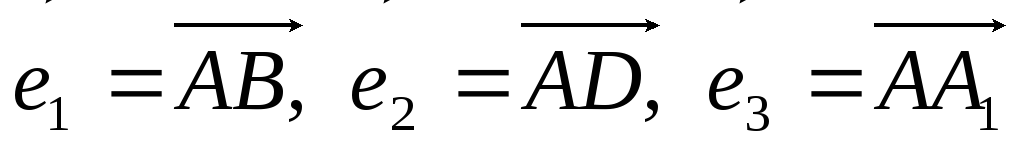 .
. -
Н
Рис. 4
ехай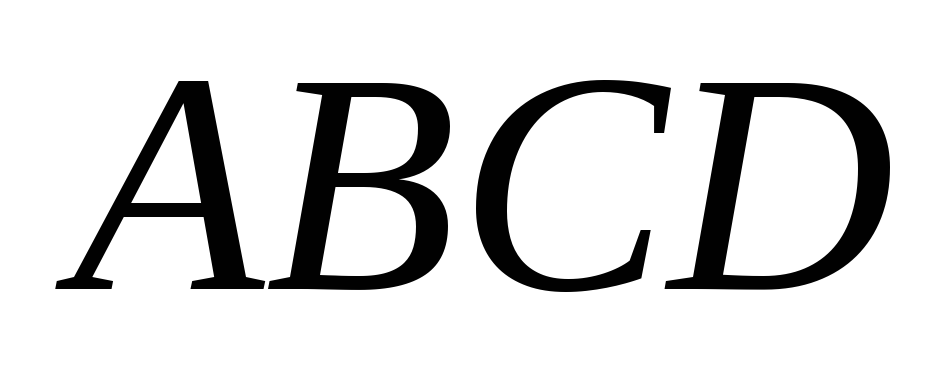 - паралелограм,
- паралелограм,
 і
і
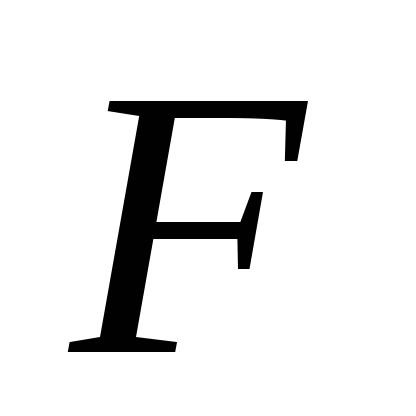 - середини протилежних сторін
- середини протилежних сторін
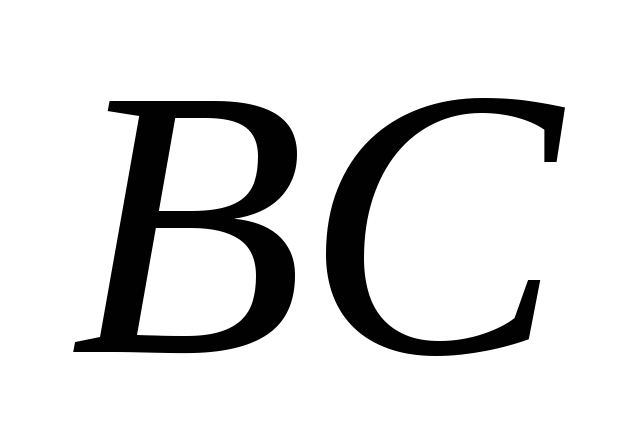 і
і
 ,
а точка
,
а точка
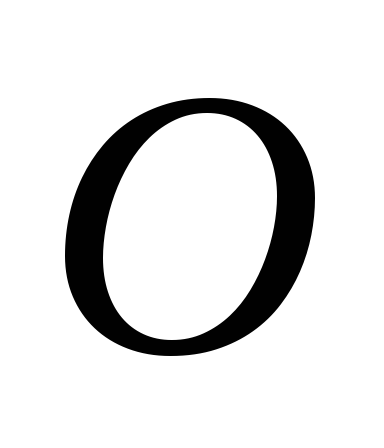 - точка перетину діагоналей. Прийнявши
вектори
- точка перетину діагоналей. Прийнявши
вектори
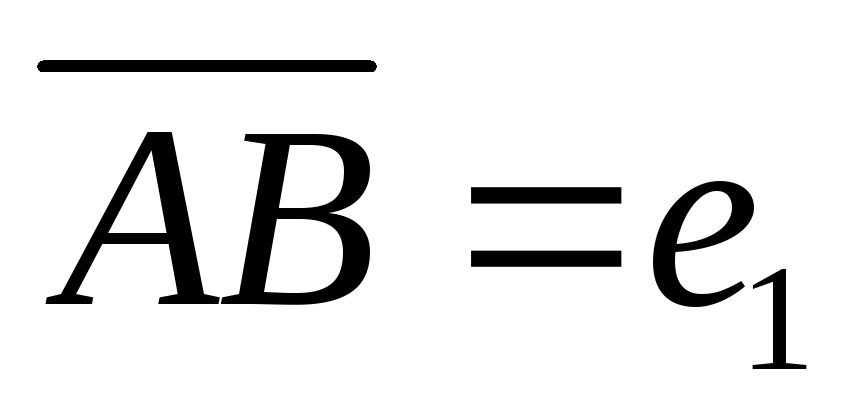 та
та
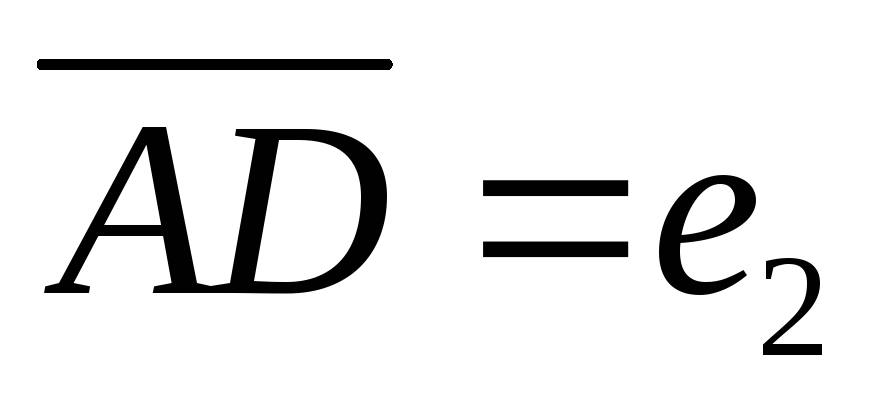 за базисні визначити координати векторів
за базисні визначити координати векторів
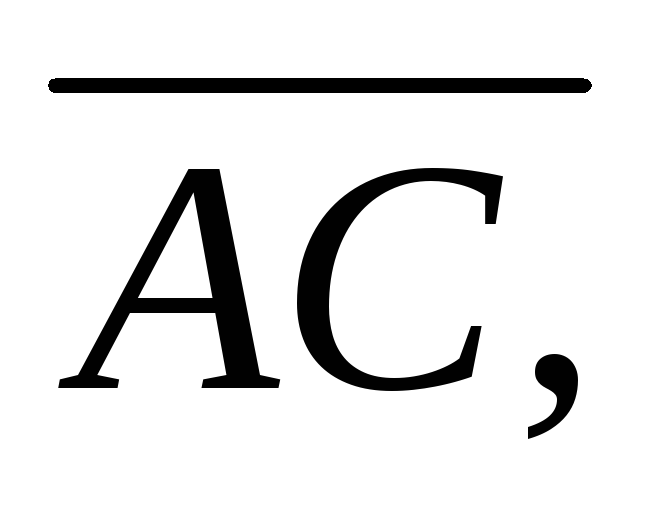
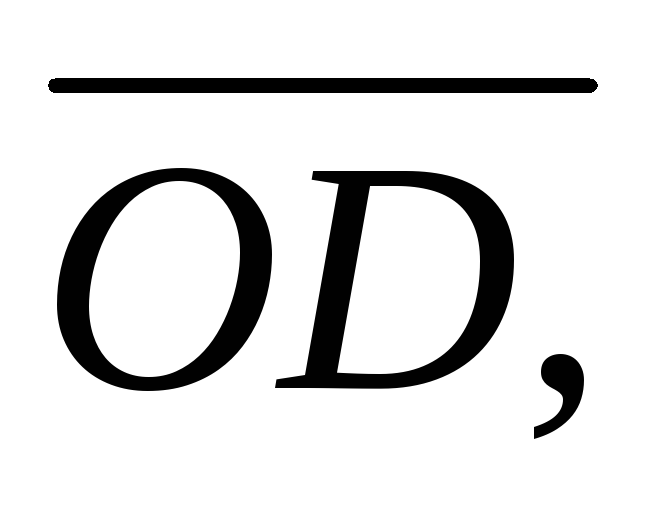
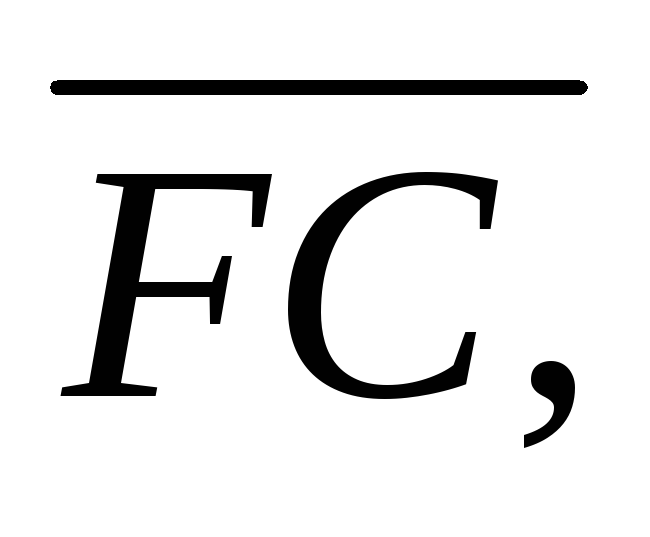
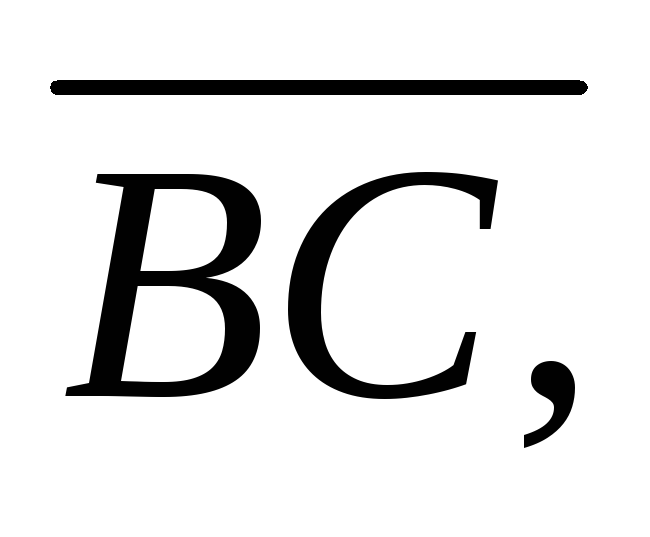
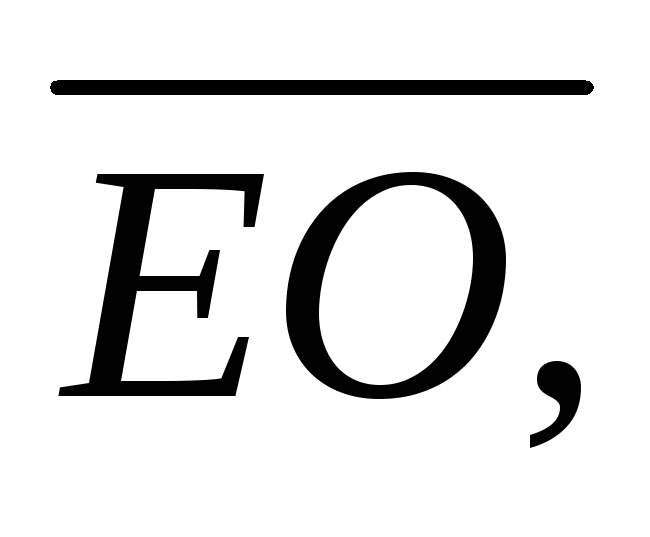
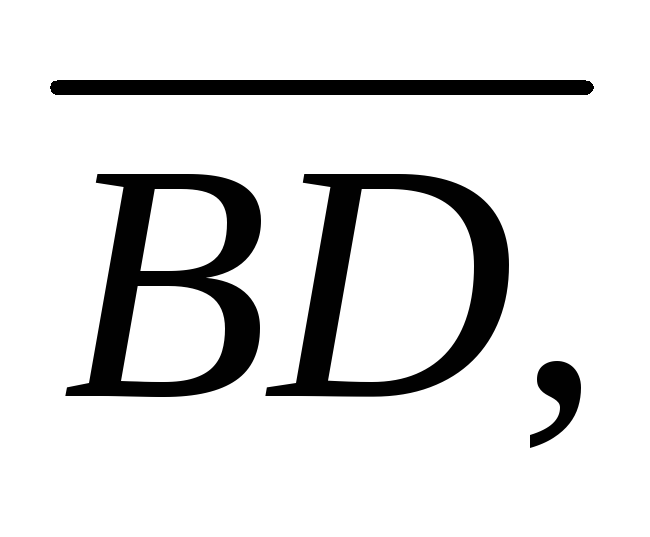

-
Дано
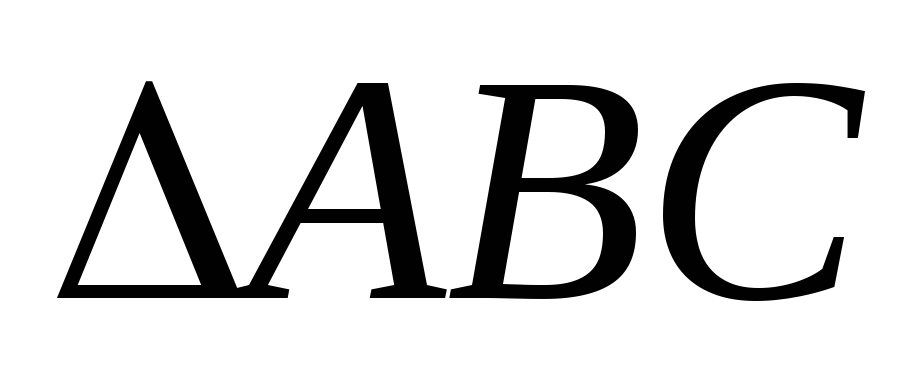 .
Прийнявши за базисні вектори
.
Прийнявши за базисні вектори
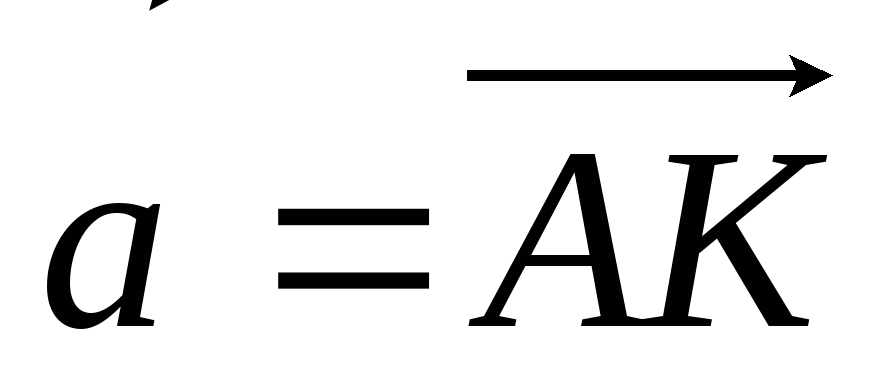 ,
де
,
де
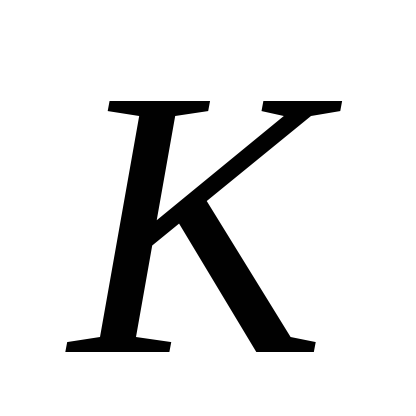 - середина
- середина
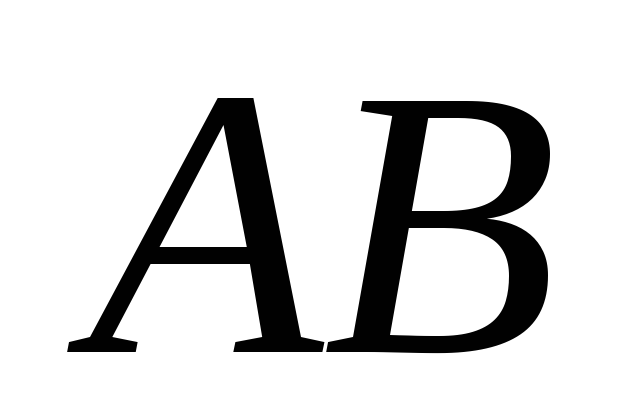 і
і
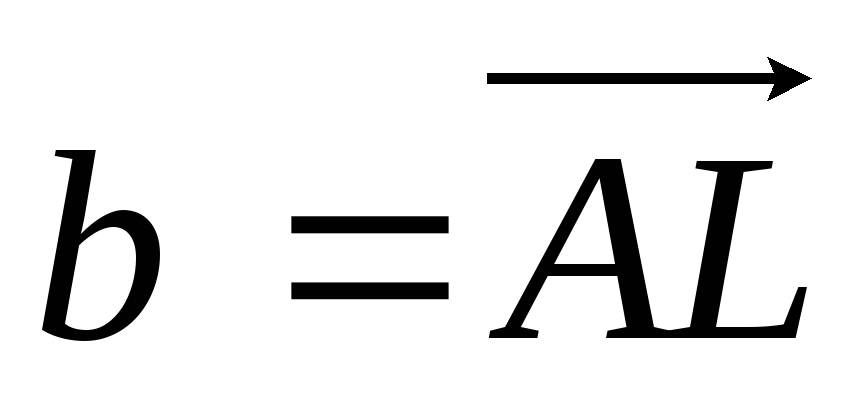 ,
де
,
де
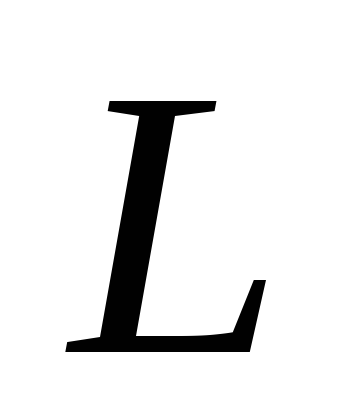 - середина
- середина
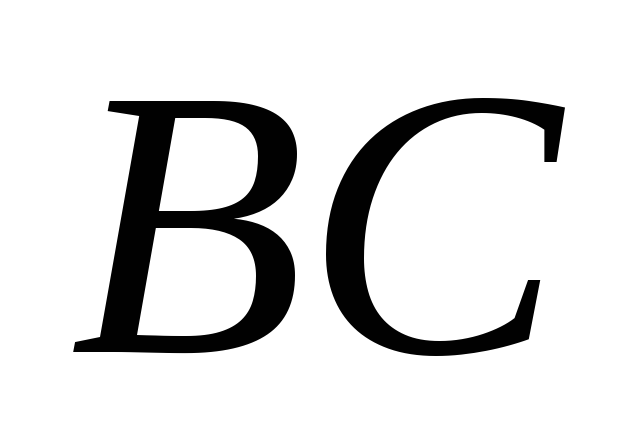 ,
виразити через них вектори
,
виразити через них вектори
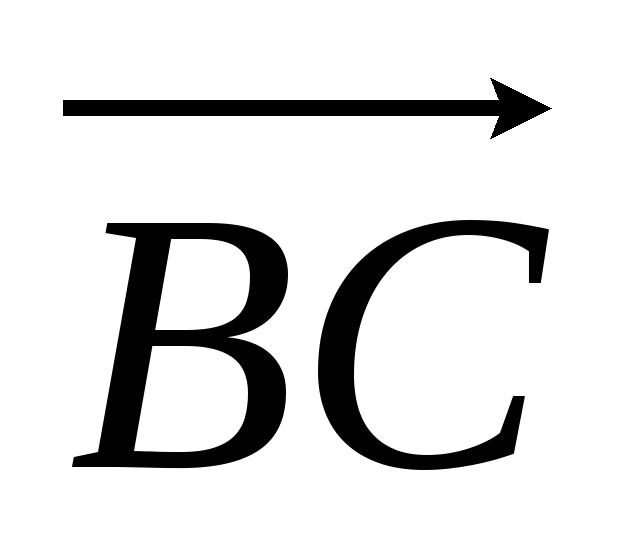 та
та
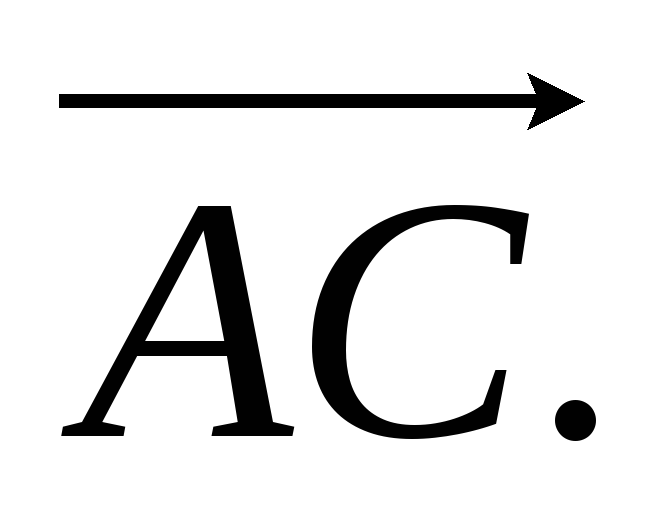
-
Дано трикутник ОАВ. Сторона АВ поділена точкою Р у відношенні АР:РВ=m:n. Розкласти вектор ОР за векторами
 та
та
 .
. -
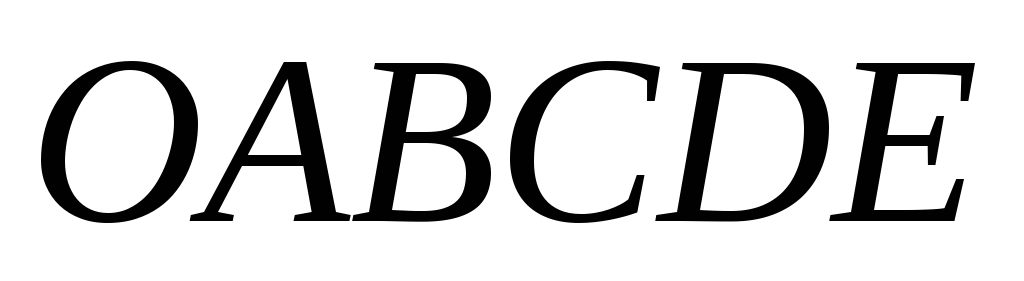 - правильний шестикутник. Вибравши
вектори
- правильний шестикутник. Вибравши
вектори
 і
і
 за базисні, виразити через них вектори
за базисні, виразити через них вектори
 ,
,
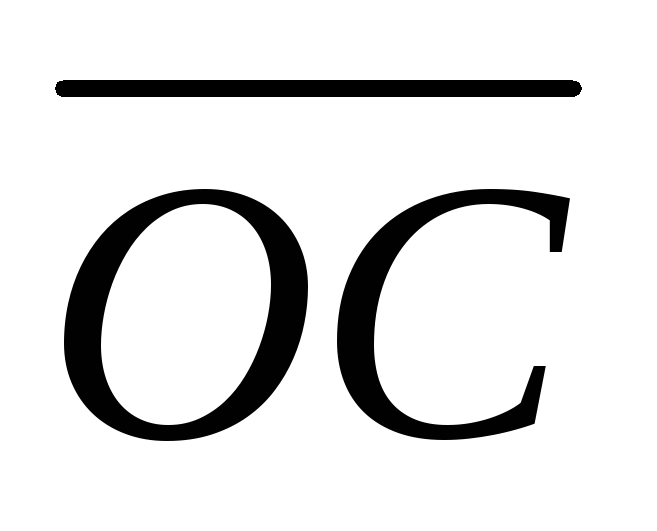 та
та
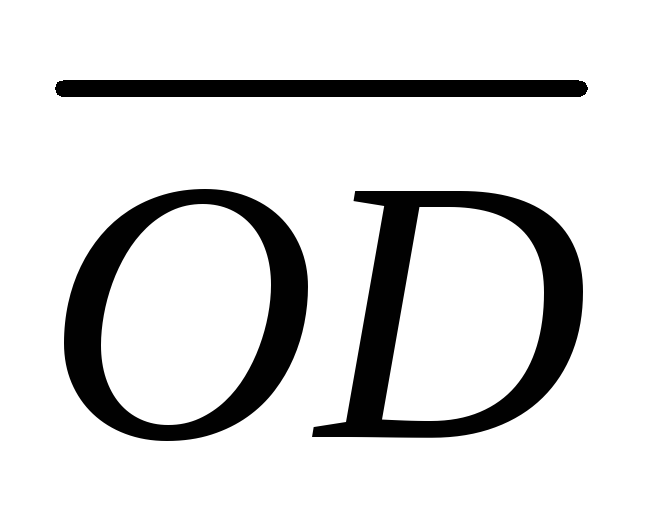 .
. -
На векторах
 ,
,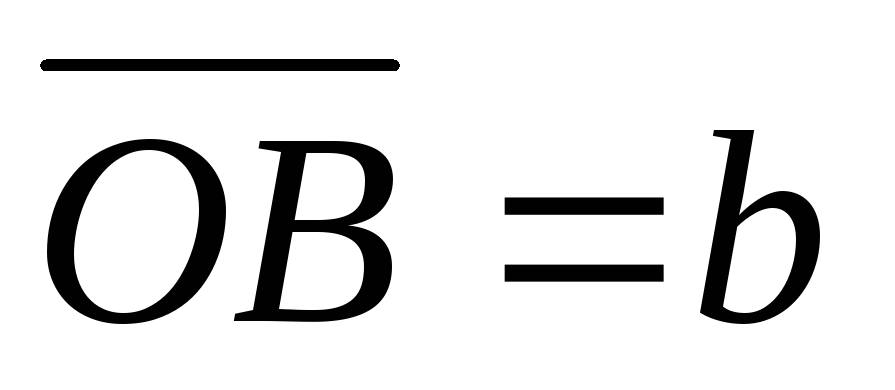 та
та
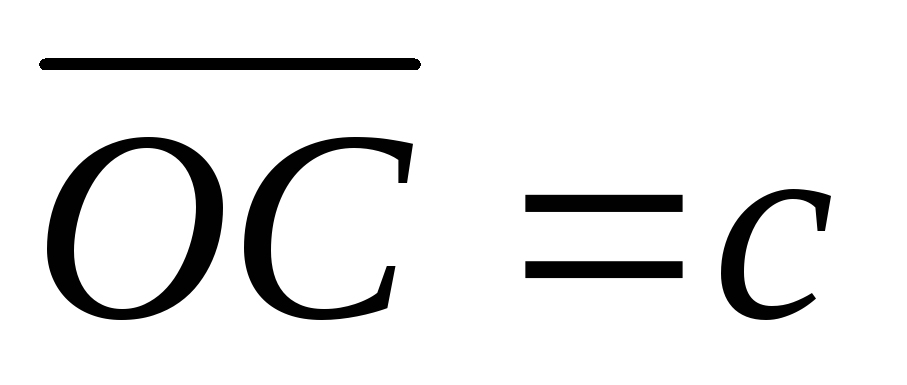 побудовано паралелепіпед. Точка М -
центр грані, яка проходить через точку
С паралельно до векторів
побудовано паралелепіпед. Точка М -
центр грані, яка проходить через точку
С паралельно до векторів
 і
і
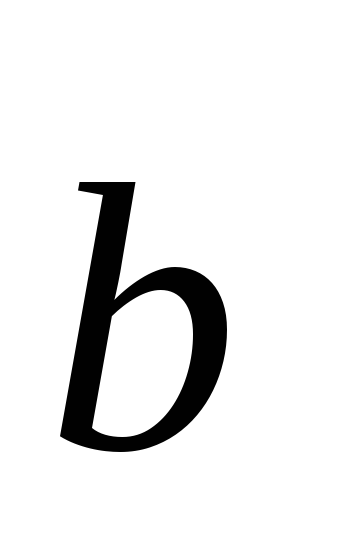 .
Розкласти вектор
.
Розкласти вектор
 за векторами
за векторами
 ,
,
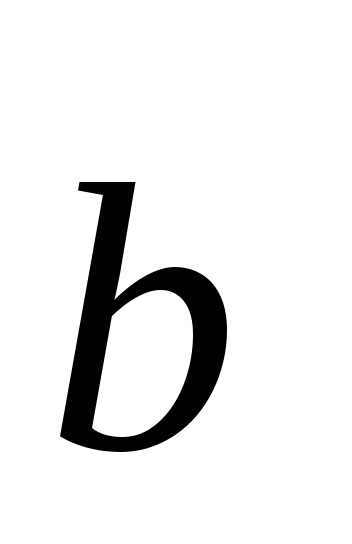 та
та
 .
. -
Дано
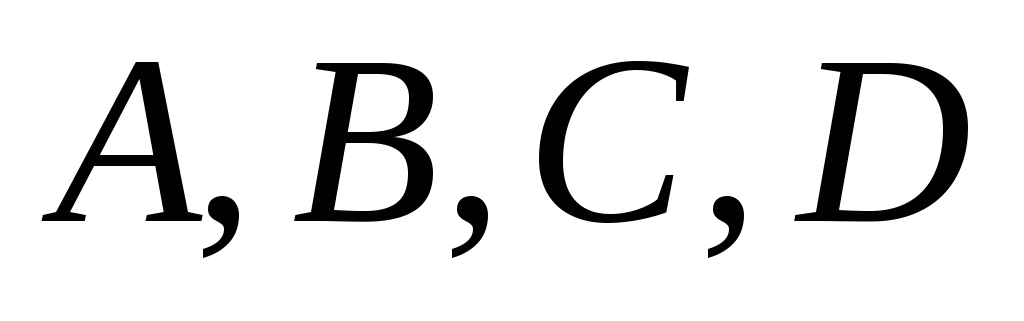 - чотири довільні точки простору.
Прийнявши за базисні вектори
- чотири довільні точки простору.
Прийнявши за базисні вектори
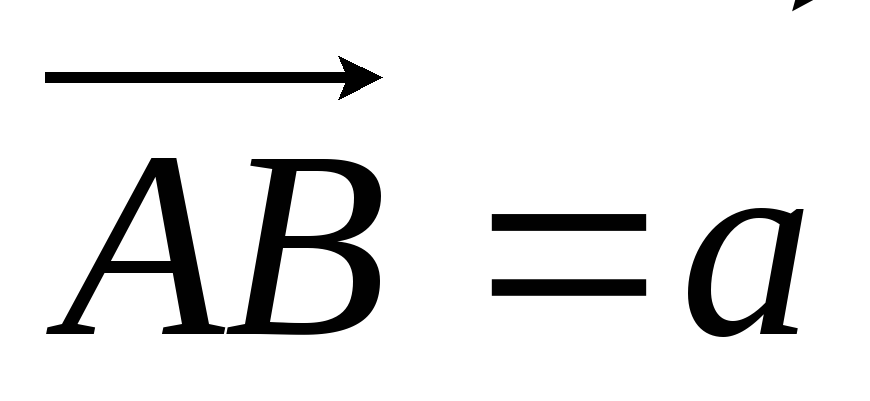 ,
,
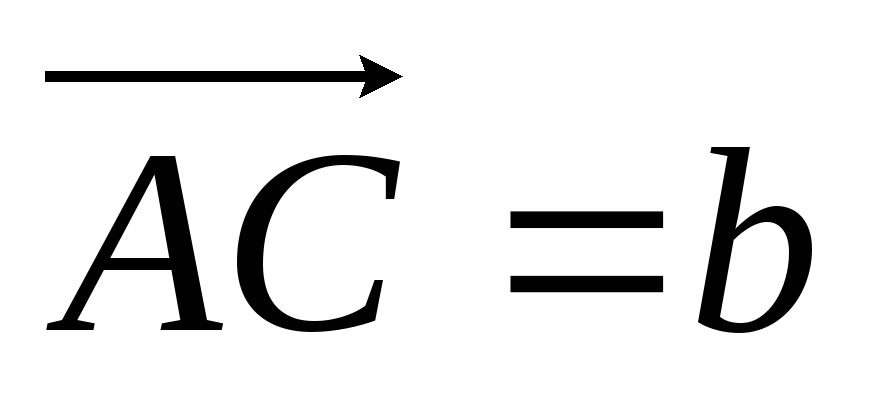 та
та
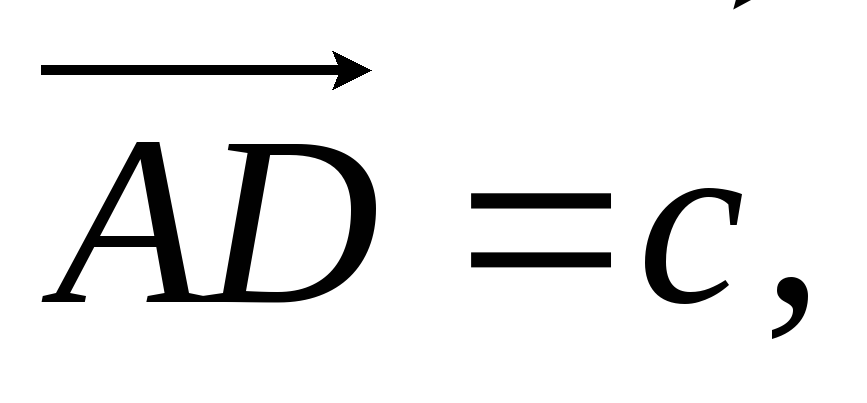 виразити через них вектор
виразити через них вектор
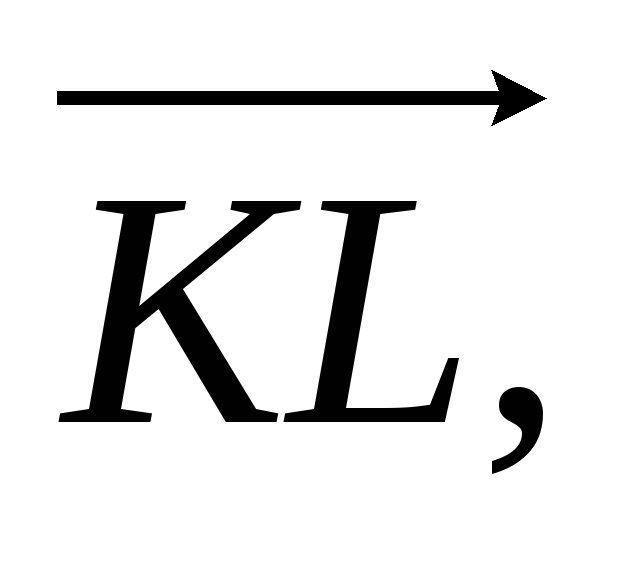 де
де
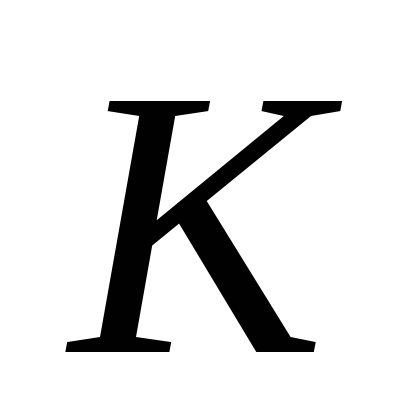 - середина
- середина
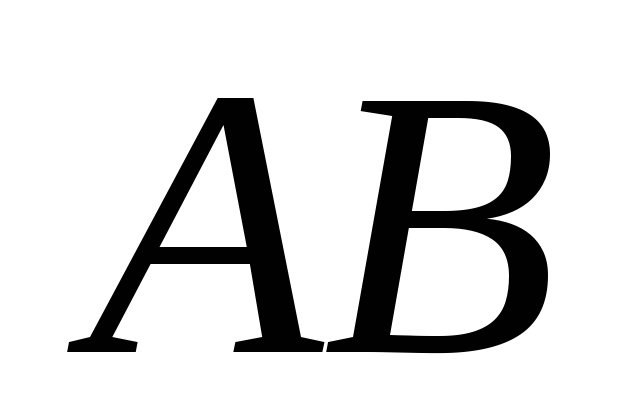 ,
,
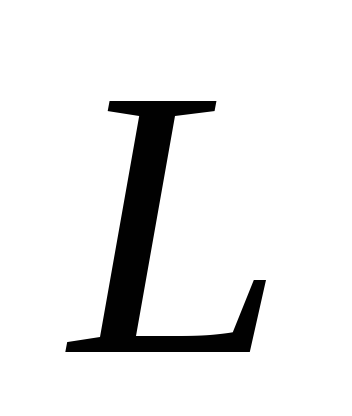 - середина
- середина

-
У трикутнику
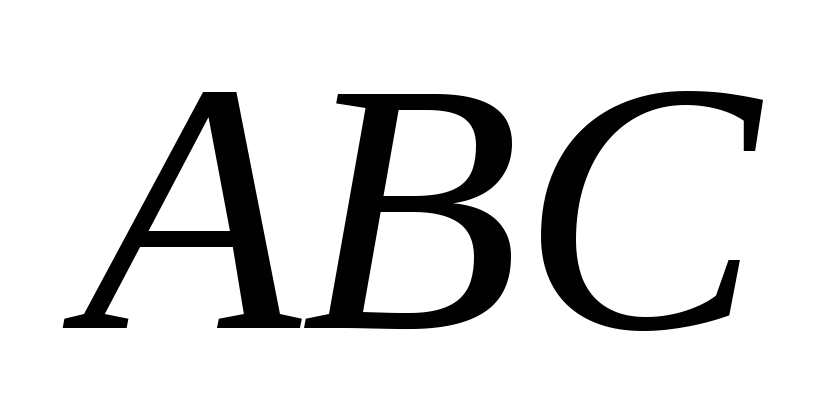 проведені медіана
проведені медіана
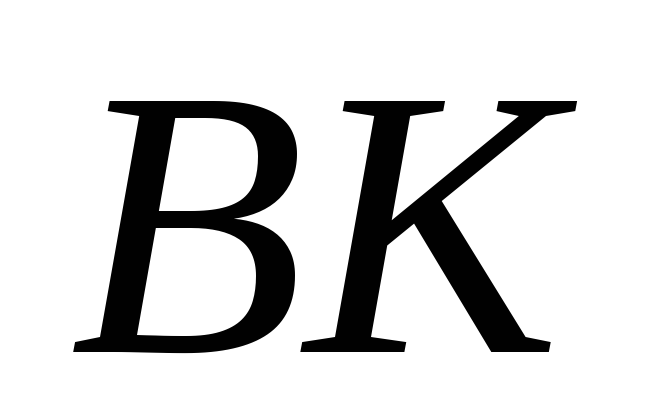 і середня лінія
і середня лінія
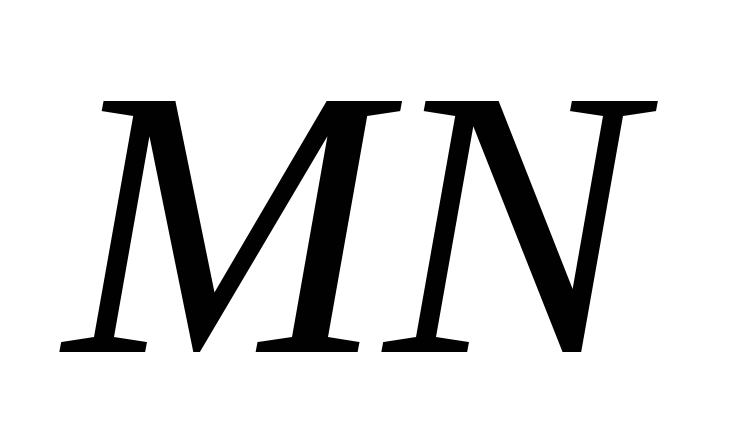 ,
яка паралельна стороні
,
яка паралельна стороні
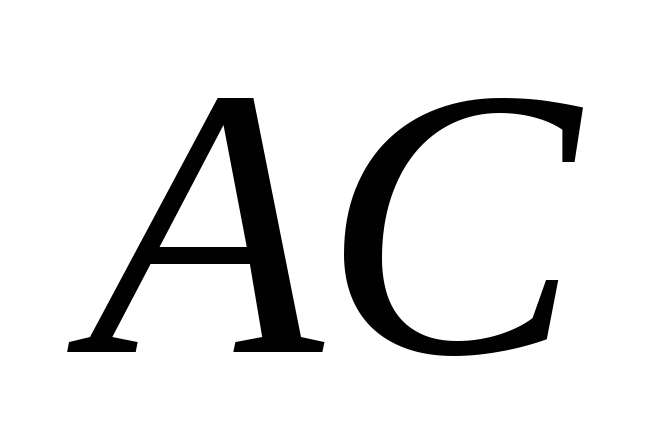 .
Прямі
.
Прямі
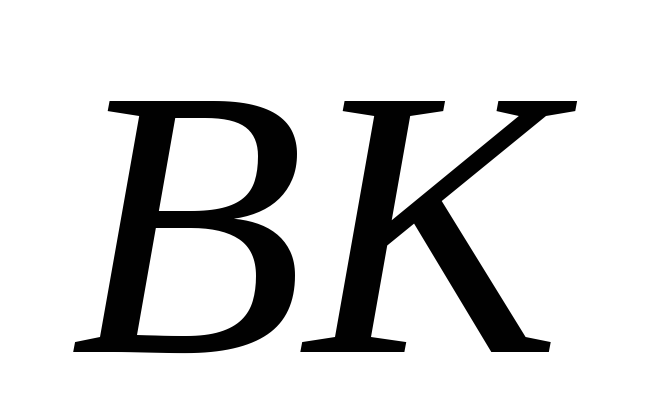 і
і
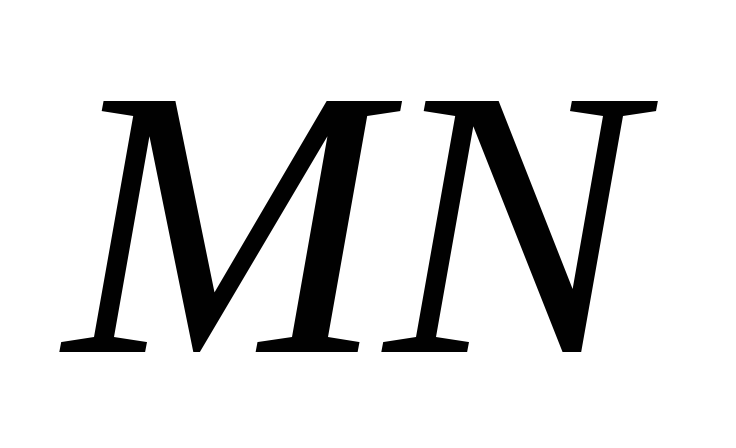 перетинаються у точці
перетинаються у точці
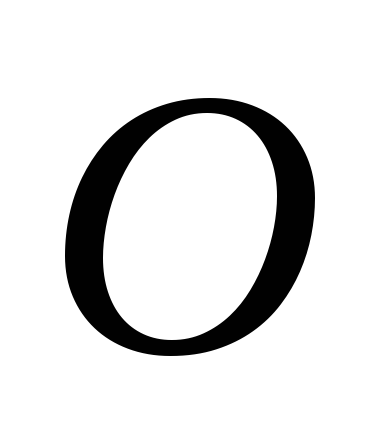 .
Знайти координати векторів
.
Знайти координати векторів
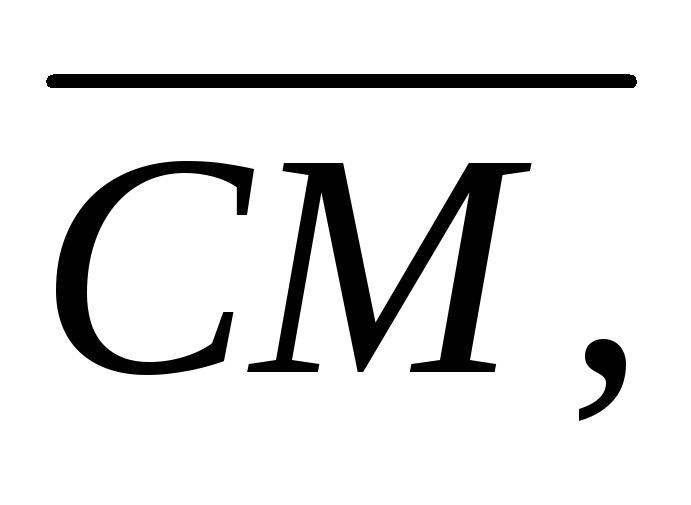
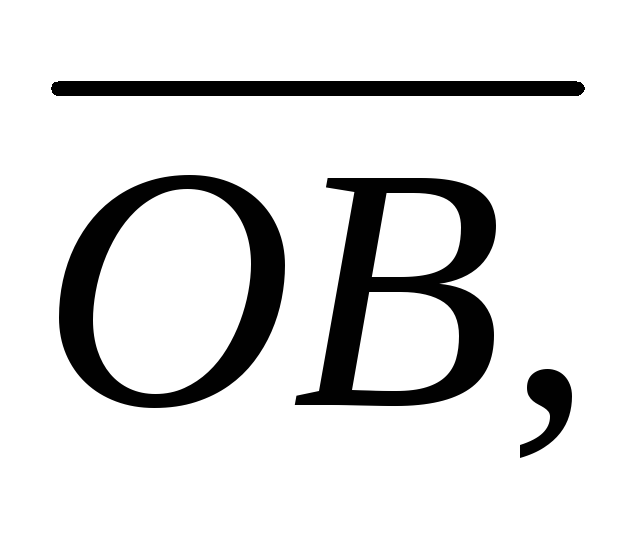
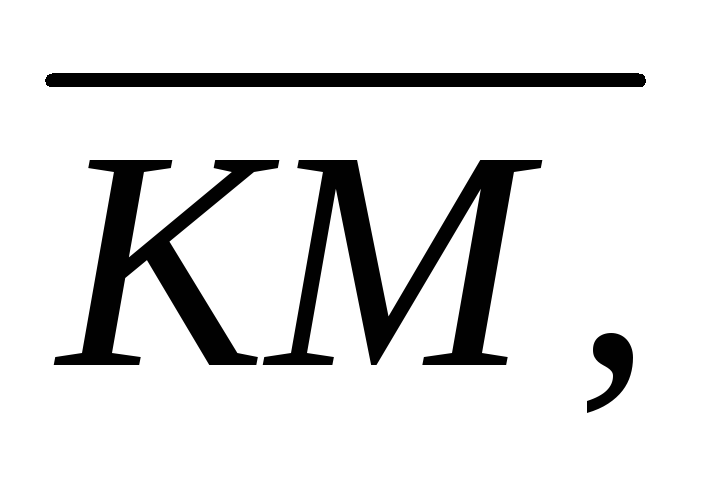
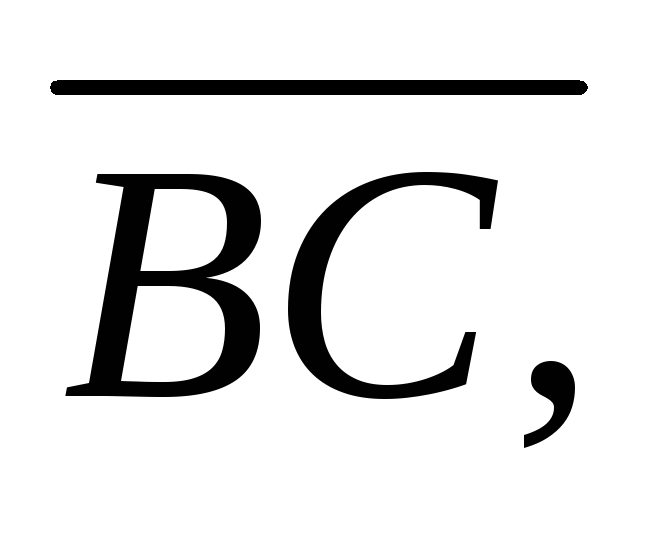
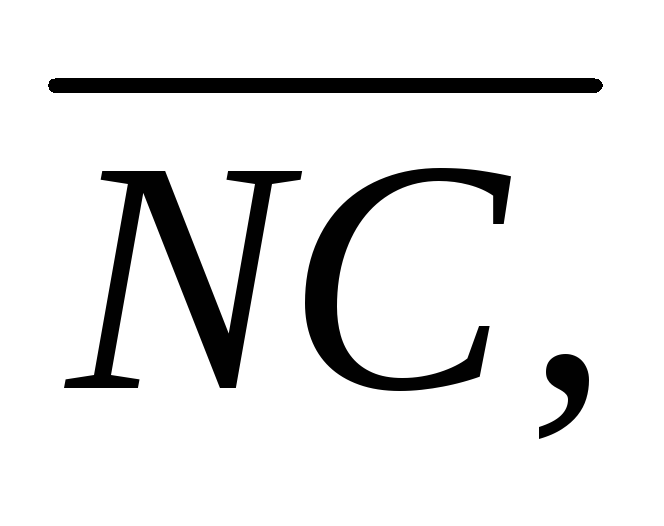
 прийнявши вектори
прийнявши вектори
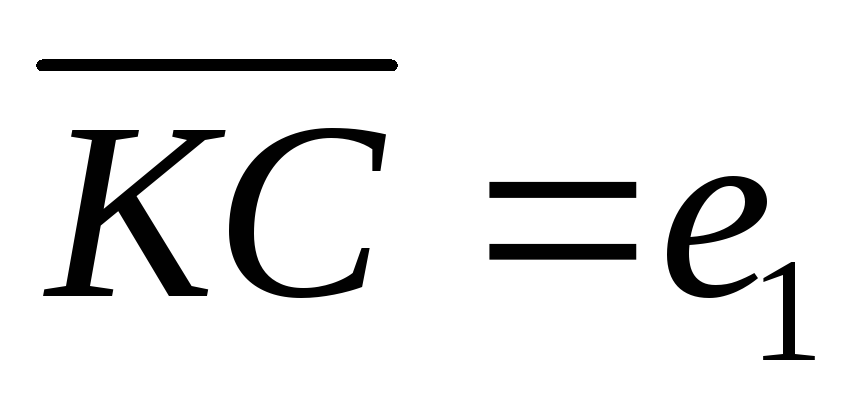 і
і
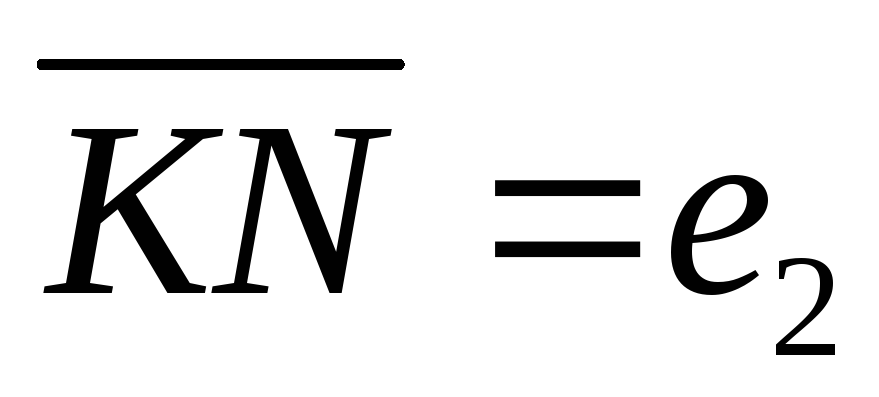 за базисні.
за базисні. -
Вектори
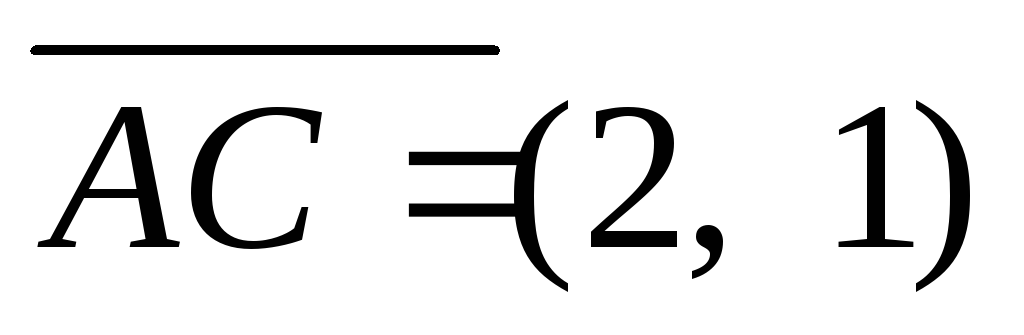 і
і
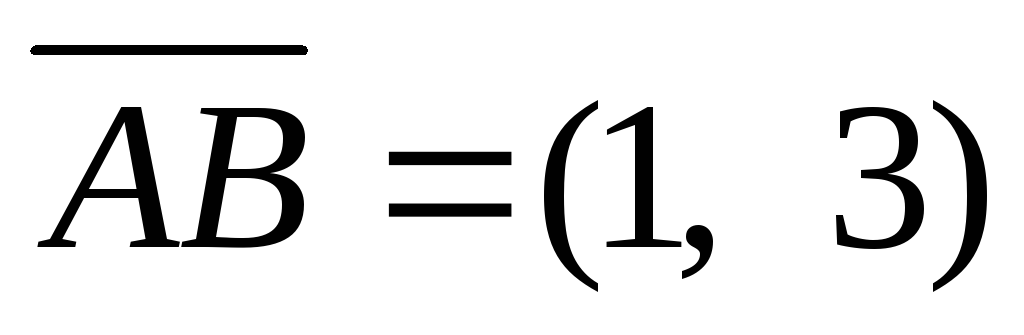 співпадають з сторонами трикутника
співпадають з сторонами трикутника
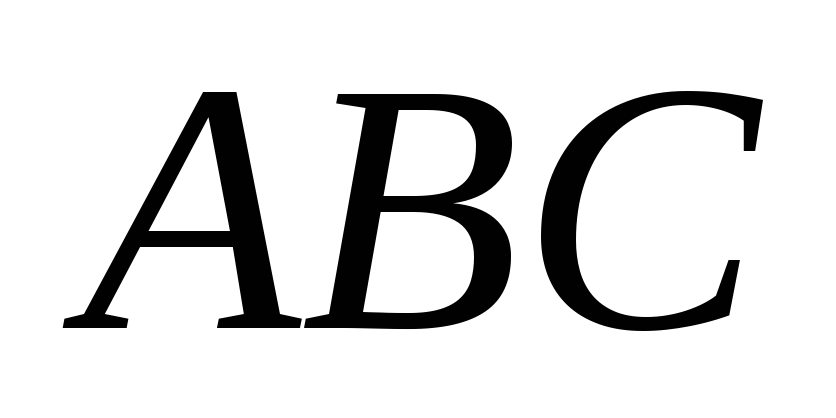 .
Визначте координати векторів
.
Визначте координати векторів
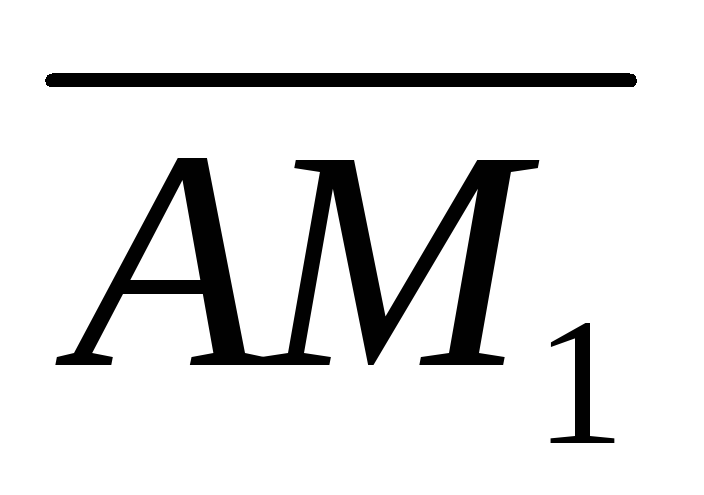 ,
,
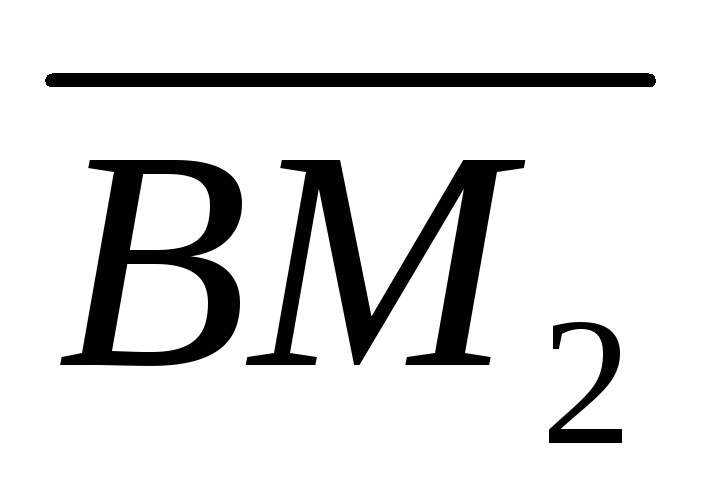 та
та
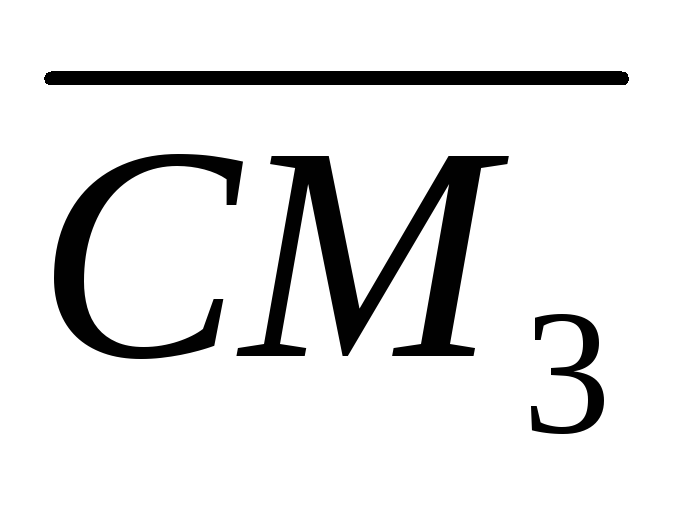 ,
які співпадають з медіанами трикутника.
,
які співпадають з медіанами трикутника. -
Серед векторів
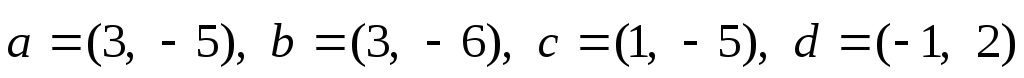 знайти лінійно залежні.
знайти лінійно залежні. -
Визначити модулі суми і різниці векторів
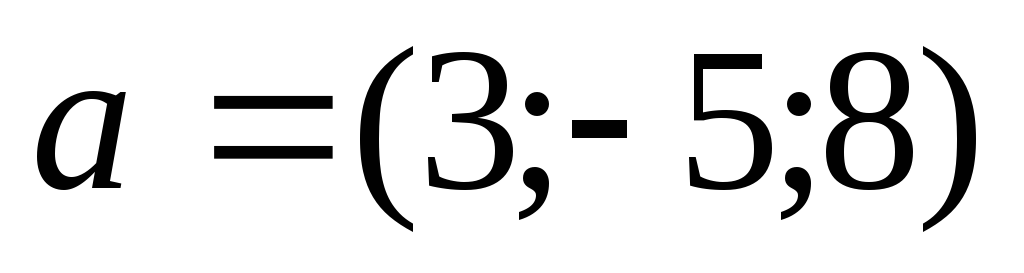 та
та
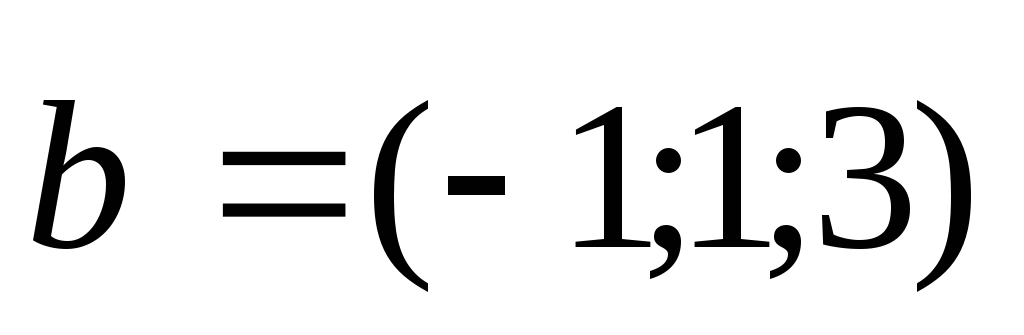 .
. -
При яких значеннях параметрів
 та
та
 вектори
вектори
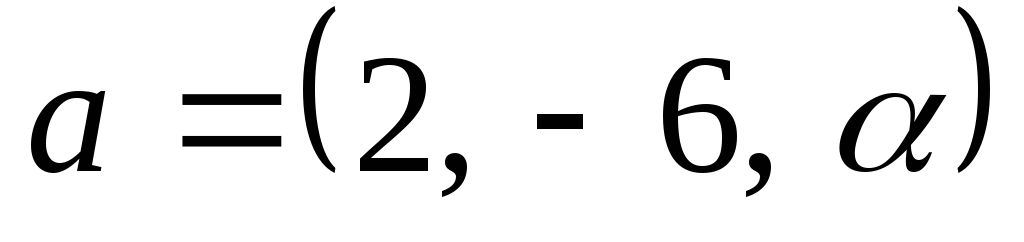 та
та
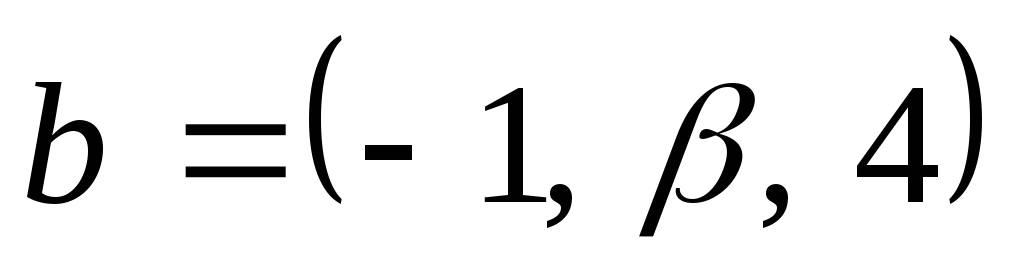 будуть колінеарні?
будуть колінеарні?
