Министерство здравоохранения Республики Беларусь Минский государственный медицинский институт

Г.К.Ильич

ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ

Учебное пособие для студентов медицинских ВУЗов

МИНСК, 1998 г.

(х2 стремится к х1), то секущая вырождается в касательную к графику функции в точке А,

имеющую угол наклона к оси абсцисс α 0:

Таким образом, тангенс угла между касательной, проведенной к графику функции в

данной точке, и осью абсцисс, числено равен значению производной функции в данной точке. В этом и состоит геометрический смысл производной.

Кфизическому смыслу производной подойдем из рассмотрения механического

движения. Если за время t тело проходит путь S, то средняя за это время скорость движения:

Но на пути S скорость может иметь различные мгновенные значения (vмгн), которые опре-

деляются как предел отношения S к t при t→0:

Следовательно, мгновенная скорость движения в данной точке представляет со-

бой значение в данный момент времени производной от пути по времени. Итак, производная имеет смысл скорости некоторого процесса.

Если рассматривается ускорение (а) механического прямолинейного движения, то мгновенное ускорение представляет собой первую производную от скорости или вторую производную от пути:

Таким образом, вторая производная имеет физический смысл ускорения.

3

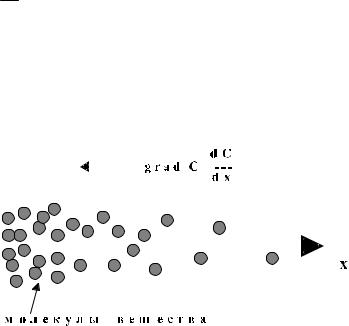
Если некоторая величина у зависит от пространственной координаты х, то произ-

водная dydx характеризует скорость пространственного изменения у. Упрощенно, производ-

ные по пространственной координате называют градиентами. Поясним смысл градиента. Представим, что некоторое вещество, аккумулируемое в биологической ткани, имеет нерав-

dCdx , или градиентом концен-

трации. Градиент некоторой величины направлен в сторону ее возрастания. Градиент

концентрации является причиной и количественной мерой диффузии, заставляя молекулы вещества перемещаться в направлении, противоположном направлению градиента.

Перенос тепла в некотором направлении (теплообмен) осуществляется за счет наличия градиента температуры; движение заряженных частиц побуждается градиентом потенциала и т. п. Таким образом, градиенты являются одной из первопричин обменных процессов, происходящих в биологических системах.

В заключение этого раздела отметим, что правила и приемы дифференцирования, применение производных для исследования функций (нахождение экстремумов функций) изучались в курсе средней школы и читателям предлагается повторить их самостоятельно.

2. Дифференциал функции.

Дифференциал функции (dу) - это произведение производной функции на приращение (или дифференциал) аргумента:

Аналитический смысл дифференциала заключается в том, что дифференциал dу представляет собой главную часть приращения функции. При малых приращениях можно счи-

тать dу ≈ у.

4

Из смысла дифференциала следует его важное практическое значение: нахождение дифференциала функции позволяет определить, насколько изменилась функция, если произошли небольшие изменения переменной, от которой она зависит.

Пример. Имеется куб с длиной ребра l=1м. На какую величину V изменится объем куба, если длина ребра увеличилась на l=1см?

Эту задачу можно, конечно, решить и методами элементарной математики:

V= (l+ l) 3- l3.

Однако, даже в этом элементарном примере необходимо выполнять довольно значительные вычисления.

Учитывая, что приращение объема куба (функции) при малых изменениях длины его ребра (аргумента) примерно равно дифференциалу объема, получим:

V ≈ dV =(l3)’· l = 3l2 l = 3·1·0,01=0,03м3.

3. Частные производные

Понятие производной было введено для функции одной переменной. Но чаще возникает необходимость количественного описания процессов, которые зависят от целого ряда параметров. Обозначим, например, состояние организма как некоторую функцию U. Очевидно, что она зависит от целого ряда параметров: x1, х2, х3, х4, ...., хn. Здесь х1 может означать температуру тела, х2 - систолическое давление, х3 - содержание гемоглобина в крови и т.д. Задача выбора информативных и доступных измерению параметров и, особенно, установления характера функциональной зависимости U(x1, х2, х3, х4, ...., хn) весьма сложна. Однако, совершенно очевидно, что математический аппарат для описания процессов жизнедеятельности должен базироваться на применении и исследовании функций многих переменных. Каким образом в этом случае трансформируется понятие производной функции? Для этого вводится понятие частной производной.

Частная производная характеризует скорость изменения функции по одной из независимых переменных, в то время как остальные переменные считаются неизменяющимися.

5

Аналогично, частная производная функции U (x,y) по переменной y:

рованной, т.е. обращается со множителем sin y как с постоянной величиной:

∂∂ Ux = 3x2 siny.

Аналогично, при прохождении частной производной по y постоянным считаем множитель х3 и находим производную от sin y:

∂U

∂x = x3cos y.

4. Частные дифференциалы и полный дифференциал

Возьмем, для упрощения, функцию двух переменных: U(x,y). Частным дифференциалом по x (обозначение dxU) называют произведение ее частной производной по x на диффе-

∂ U

d yU = ∂ y dy.

Частные дифференциалы позволяют оценивать, насколько изменится значение функции, если изменится на небольшую величину один из соответствующих ее аргументов.

Сумма всех частных дифференциалов называется полным дифференциалом. Для функции U(x,y) ее полный дифференциал (dU) равен:

6

Нахождение полного дифференциала позволяет оценить, насколько изменится значение функции при изменении всех переменных, от которых она зависит.

Пример. Несколько усложним уже рассматривавшуюся задачу по нахождению изменения объема куба при увеличении длины его ребра. Возьмем параллелепипед с длинами

Решение этой задачи может быть выполнено и без применения аппарата высшей математики:

V=(l1+ l1) (l2+ l2) (l3+ l3) – l1 l2 l3.

Однако, использование полного дифференциала позволяет существенно упростить решение и вычисление сделать минимальными. Поскольку изменения длин ребер не велики по сравнению с их первоначальными значениями, будем считать, что искомое приращение

V объема V (функции трех переменных - длин ребер) примерно равно полному дифференциалу dV:

ных производных для рассмотрения задач фармакологии.

Упрощенно, будем считать, что реакция организма на введенный лекарственный препарат зависит от величины его дозы x и времени t, прошедшем после введения. То есть, реакцию организма будем характеризовать некоторой функцией R(x,t). Допустим, далее, что эта функция имеет вид:

7

симуму. Если, например, в уравнении (9) время определялось в часах, то максимальная реакция наступит через 2 часа.

5.Первообразная функция и неопределенный интеграл

Вэлементарной математике сложение и вычитание, умножение и деление, возведение

встепень и извлечение корня - примеры взаимообратных математических операций. Последовательно примененные к одному и тому же числу эти операции самого числа не изменяют.

a b = а, n an = а). b

Взаимообратные операции существуют и в высшей математике. Дифференцирование ( нахождение производной) позволяет по некоторой заданной функции найти скорость ее изменения. Операцией, обратной дифференцированию, является интегрирование - нахождение самой функции (первообразной) по заданной скорости ее изменения.

Функция F(х) называют первообразной функции f(х), если для всех х из области определения функции F ′ (х) = f(х) или dF(х) = f(х) dх.

Иными словами, первообразная функция - это такая, производной от которой является заданная.

Например, задана функция f (x) = 2х. Ее первообразной будет F(x) = х2 , так как F

′(х) = f(х) = 2х. Однако, F(х) = х2 + C, где C - произвольная постоянная , так же будет первообразной для f(х) = 2х, поскольку (х2 + С )′ = 2х.

Совокупность всех первообразных функций для заданной функции f(х) называют

неопределенным интегралом и обозначают : ∫ f (x)dx = F(x) +C .

9

6.Определенный интеграл

К понятию определенного интеграла подойдем из рассмотрения геометрической зада-

чи.

Допустим, что некоторая функция задана в виде графика (см. рис.3 ). Поставим зада-

Приближенно, значение искомой площади можно найти, разбив криволинейную трапецию на отдельные прямоугольники и сложив их площади. Основанием этих прямоуголь-

Соотношение (12) выполняется тем точнее, чем меньше основания прямоугольников

хi. Точное же значение искомой площади будет найдено при предельном переходе:

10