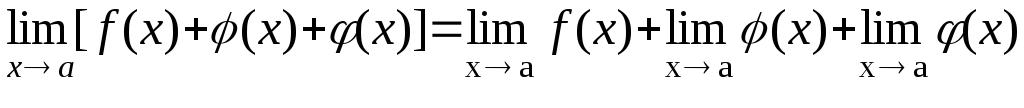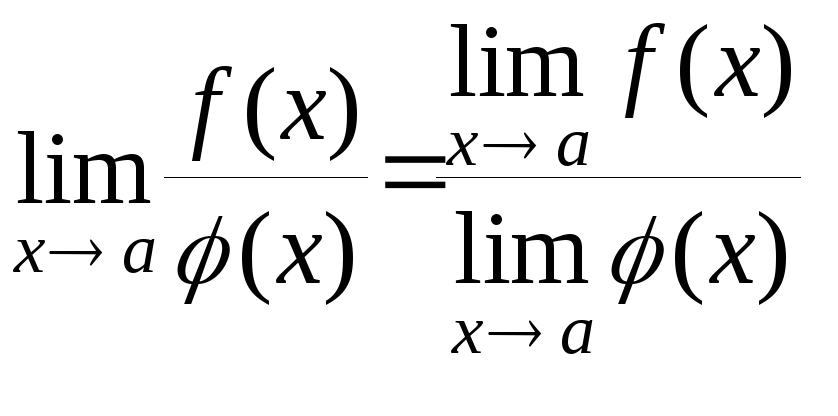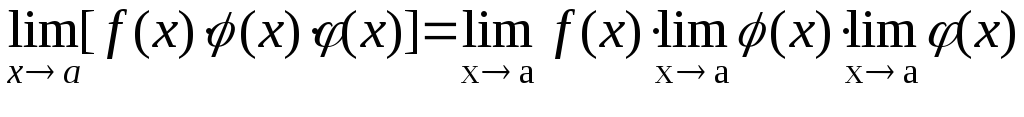1

Функция y = f(x) имеет пределом

число А при стремлении х к а, если для каждого числа е>0 найдется такое число δ>0, что

|y — A|<е, при | х —a|<δ

2

Математическая запись предела

3

Предел постоянной величины

4

Предел суммы (разности) конечного числа функций

5

Предел частного двух функций

6

Предел произведений конечного числа функций

при lim f(x) и lim φ(x) и lim ф(x) ≠0

7

замечательный предел:

8

замечательный предел:

1

Производной функции f(x) называется предел отношения приращения функции

Δу=f(x+Δx)-f(x)

к приращению аргумента

Δх=x-x₀

в точке х при стремлении Δх к нулю.

Процесс нахождения производной называется дифференцированием, поэтому выражение «продифференцировать функцию» равносильно выражению «найти производную функции».:

2

Математическая запись производной

3

Производная функции y = f(x): имеет физический смысл (в том числе механический) мгновенной скорости процесса

4

Производная функции y = f(x): имеет геометрический смысл.

Угловой коэффициент касательной к графику функции в данной точке равен значению ее производной в точке касания. В этом и состоит геометрический смысл производной

5

Общее правило дифференцирования.

При дифференцировании функции (нахождении ее производной) придерживаются следующие схемы:

1. выбрав некоторое значение х, дают ему приращение х и находят значение функции в точке х + х, равное f(x + x);

2. определяют приращение функции: f = f(x + x)-f(x);

3. составляют отношение f / x и, если возможно, упрощают его;

4. находят производную функции, то есть предел

отношения приращения функции Δу=f(x+Δx)-f(x) к приращению аргумента Δх=x-x₀ в точке х при стремлении Δх к нулю т.е.

если этот предел существует.

6

Таблица производных элементарных функций

Производная постоянной величины у=С:

ý= 0;

7

Производная степенной функции

у = х^μ:

ý=μx^μ-1

8

Производная показательной функции у = а^x: в частности, если у = е^х

ý=a^xlna;

ý= е^x;

9

Производная

логарифмической функции y=log_ax

10

Производная

натурального логарифма у = lnх

11

Производная тригонометрической функции y=sinx

y'=cosx;

12

Производная тригонометрической функции y=cos x

ý =- sin x;

13

Производная тригонометрической функции y = tgx

14

Производная тригонометрической функции y = ctgx

15

Производная обратной тригонометри

ческой функции y=arcsinx

16

Производная обратной тригонометри-ческой функции y=arccosx

17

Производная обратной тригонометри-ческой функции y=arctgx

18

Производная обратной тригонометри-ческой функции y=arcctgx

19

Производная суммы (разности) функций y = w±u

y' = u'±v'

20

Производная произведения двух функций y=uv y' = u'v + v'u.

21

Производная частного двух функций y=u/v

22

Производная сложной функции

y = f₁(u), если u = f₂(x),

у'_x = у'_иu'_x

23

Производная неявной функции

При задании функции в неявном виде F(х, у)=0 можно рассматривать левую часть равенства F(x, у) как некоторую сложную функцию х и дифференцировать обе части равенства, имея при этом в виду, что у есть функция от х, обращающая соотношение F(x, у) =0 в тождество.

24

Производные второго и высших порядков

Производная y_x'= f '(x) от функции

y=f(x) тоже является функцией от х; и также может быть дифференцируема.

Производная от производной называется производной вто­рого порядка или просто второй производной.

y''=f ''(х)=( f '(х)) '=

Производная от производной вто­рого порядка называется производной третьего порядка и т.д. yⁿ==(f^n-1(х)) '

25

Частные производные функции нескольких переменных

z = f(x,y).

Частные производные первого порядка. Частной производной первого порядка функции z = f(x,y) по аргументу х в рассматриваемой точке (х; у) называется предел

если он существует.

Частная производная функции

z = f(x, y) по аргументу х обозначается одним из следующих символов:

Аналогично частная производная по у обозначается

и определяется формулой:

Так как частная производная – это обычная производная функции одного аргумента, то ее нетрудно вычислить. Для этого нужно пользоваться всеми рассмотренными до сих пор правилами дифференцирования, учитывая в каждом случае, какой из аргументов принимается за «постоянное число», а какой служит «переменной дифференцирования»

Применение производных для исследования функций

1

Условие возрастания функции

y = f(x) на отрезке [а, b]

f '(x)>0

2

Условие убывания функции y=f(x) на отрезке [а, b]

f '(x)<0

3

Условие максимума функции y=f(x) при x= а

f '(a)=0 и f '' (a)<0

4

Условия функции экстремума

Если при х=а производные f '(а) = 0 и f "(а) = 0, то необходи­мо исследовать f '(x) в окрестностях точки x = а. Функция у=f(х) при х=а имеет максимум, если при переходе через точку х= а производная

f '(x) меняет знак с «+» на «-», в случае минимума — с « - » на «+» .Если

f '(x) не меняет знака при переходе через точку х = а, то в этой точке экстремума функ­ции нет