Разложение функции в степенные ряды

Любая функция, бесконечно дифференцируемая в заданном интервале, может быть разложена в этом интервале в сходящийся к ней бесконечный степенной ряд.

Пусть функция есть суммой степенного ряда по степеням разности, который сходится в некотором интервале:

Тогда в интервале сходимости ряд можно почленно дифференцировать любое число раз:

.

.

.

В приведенных соотношениях принимая , получим

… .

Подставляя полученные выражения коэффициентов в ряд для , получим

Полученный ряд называется рядом Тейлора функции по степеням.

При получают ряд по степеням, который называется рядом Маклорена функции.

Разность между функцией и частной суммойряда Тейлора функцииназывают остаточным членом ряда Тейлора и обозначают, т. е.

.

Остаточный член ряда Тейлора определяется следующим образом

,

Здесь .

Теорема 9.7.Для того, чтобы ряд Тейлора функциисходился к ней в некотором интервале, необходимо и достаточно, чтобы в заданном интервале сходился бы к нулю остаточный член этого ряда.

ВЫВОД: Задача разложения функции в степенной ряд сводится, по существу, к определению, при которых.

Ряды Тейлора некоторых элементарных функций

1. Ряд Тейлора для функции сходится кдля любогот. е.

.

или

.

2. Ряд Тейлора функции сходится кдля, т.е.

.

или

Здесь имеем , тогда

…

Для получим

…

Таким образом,

3. Ряд Тейлора для функции сходитсядля всех, т.е.

,

В данном случае имеем

… .

Для , имеем

Таким образом,

.

4. В отличие от рассмотренных функций , для которых ряды Тейлора в точкесходятся для любогосоответствующий ряд Тейлора для функциисходится только на интервале:

;.

Или

Задача 9.15. Разложить в ряд Маклорена функцию .

Здесь имеем:

Поскольку , то для фиксированногоимеет место неравенствопри любом. Таким образом, имеем:

Задача 9.16.Составить для функцииряд Тейлора, расположенного по степеням.

Здесь

Искомый ряд будет иметь вид

Приложения степенных рядов

Степенные ряды находят применение в различных вопросах как приближенных вычислений, так и в приближенных методах анализа. С помощью степенных рядов составляют таблицы значений функций, решают дифференциальные уравнения, вычисляют приближенные значения определенных интегралов, определяют предел функции и т.д.

Рассмотрим некоторые примеры.

Пусть необходимо найти следующий предел:

.

Здесь имеет место неопределенность . Заменимиих разложением в степенные ряды:

.

Рассмотрим следующий пример.

Необходимо вычислить определенный интеграл . Такие интегралы называются неберущимися, т. к. первообразную нельзя представить в квадратурах. В связи с отмеченным эту задачу можно решить приближенными методами с помощью формул прямоугольников, трапеций или парабол.

Здесь рассмотрим способ вычисления интегралов с помощью рядов.

Для представленной задачи разложим подынтегральную функцию в степенной ряд. Поскольку

при любом то, подставляя вместозначение переменнойполучим

В таком случае, имеют

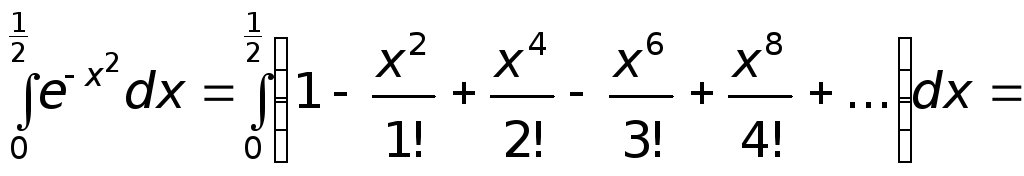
Получили знакопеременный ряд, который удовлетворяет условиям сходимости Лейбница. Таким образом, ошибка от замены суммы ряда его частной суммой по абсолютной величине будет меньше абсолютной величины первого из отбрасываемого его члена. В частном случае, положив, что интеграл равен сумме первых двух слагаемых, вносят ошибку, меньшую чем

.

Отсюда следует, что ограничиваясь только двумя слагаемыми, получают приближенное значение с точностью до :

, или.

147