Степенные ряды. Радиус сходимости. Теорема Абеля

Степенные ряды широко применяются в математике особенно при решении разнообразных задач, связанных с приближенными значениями функций, интегралов и т.д.

Определение 9.7.Степенным рядом называется ряд вида

.

В более общем виде степенной ряд задается соотношением

(9.6)

или в компактной форме , где- некоторая постоянная величина.

Если речь идет о ряде (9.5), то говорят, что он расположен по степеням , в тоже время ряд (9.6) расположен по степеням. Следует отметить, что ряд (9.6) всегда можно свести к виду (9.5), в связи с чем обычно принимают, что когда не обуславливают степенной ряд, то, имеет в виду ряд (9.5). Если ряд (9.5) сходится при, то отмечают, что степенной ряд сходится в точке.

Определение 9.8.Множество всех точек, в которых степенной ряд сходится, называется областью сходимости степенного ряда.

Степенной ряд всегда сходится при или. В связи с этим можно утверждать, что область сходимости степенного ряда будет содержать по крайней мере одну точку. Дальнейшие сведения о виде области сходимости степенного ряда получают из теоремы Абеля.

Теорема Абеля.Если степенной рядсходится в некоторой точке, то он сходится (и притом абсолютно) внутри окружности с центром ви радиусом, то есть радиусом меньше, чем расстояние отдо(рис. 9.1)

Рис. 9.1

Применяя теорему Абеля, легко можно установить, что для степенного ряда (9.5) возможно три варианта:

1) степенной ряд расходится во всех точках, кроме .

Например:

.

Такие степенные ряды практического значения не имеют;

2) степенной ряд сходится во всех точках .

Например:

Сумма такого ряда равна функции ;

3) степенной ряд сходится в одних точках, а в других - расходится.

Например:

При ряд сходится, приряд расходится. Следовательно, областью сходимости ряда будет отрезок.

Определение 9.9. Числотакое, что ряд (9.6) сходится для всех значений, которые удовлетворяют условию, и расходится для всех, удовлетворяющих неравенству, называется радиусом сходимости ряда.

Радиус сходимости степенных рядов можно отыскивать, руководствуясь следующими теоремами.

Теорема 9.5.Если у степенного ряда последовательностьимеет конечный или бесконечный пределы, то для сходимости ряда справедлива формула.

Теорема 9.6.Если последовательностьимеет конечный предел, то для радиуса сходимости справедливо соотношение

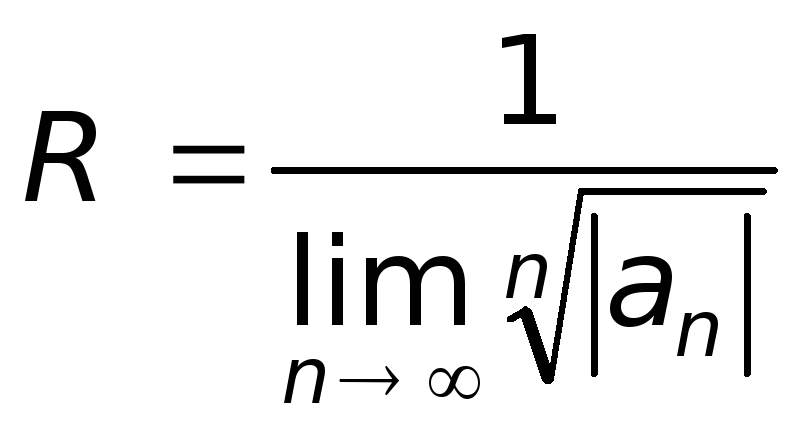
Задача 9.11.Найти радиус сходимости степенного ряда,

Для данного ряда имеем .

Тогда

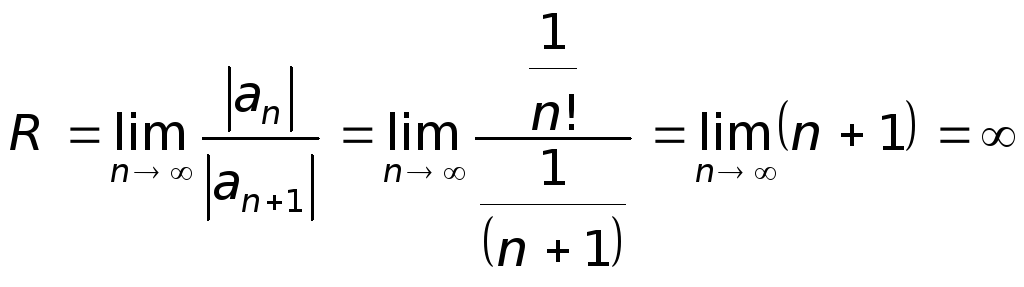
Исходный ряд сходится во всех точках .

Задача 9.12.Найти радиус и область сходимости ряда.

Здесь . При этом.

Таким образом, ряд сходится в интервале .

Рассмотрим область сходимости ряда. Для этого исследуем сходимость ряда на границах интервала .

Если , имеем ряд.

Такой ряд сходится по признаку Лейбница.

Если , то имеем ряд. Такой ряд будет расходящимся.

Таким образом, исходный ряд имеет область сходимости на промежутке .

Задача 9.13.Найти радиус сходимости ряда.

Здесь . Тогда радиус сходимости ряда определим из соотношения:

.

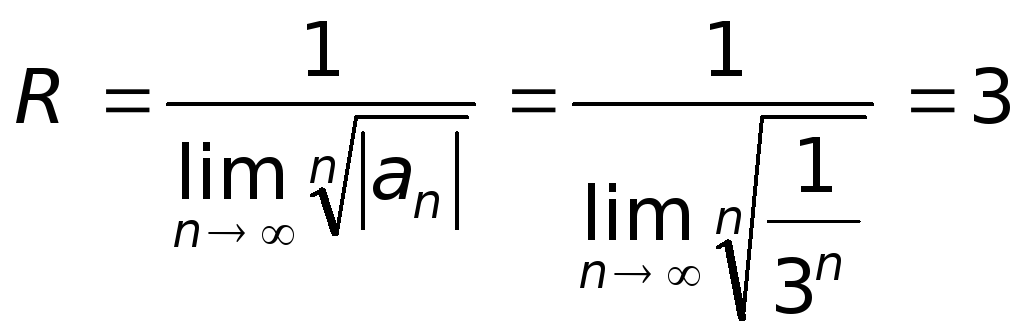Ряд сходится в интервале .

Задача 9.14.Исследовать сходимость ряда

В данном случае имеют

.

Тогда

.

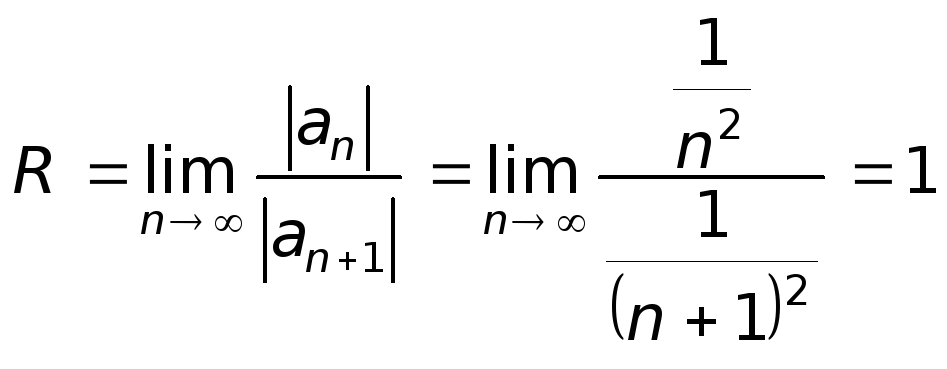Таким образом, ряд сходится, если , т.е..

Выполним исследование сходимости ряда на границах интервала.

При , имеем ряд

Этот ряд является сходящимся.

При , имеем

Этот ряд является абсолютно сходящимся.

Таким образом, исходный ряд сходится в области .