Дифференциальные уравнения
181-190. Найти общее решение дифференциального уравнения первого порядка.
181.
182.
183.
184.
185.
186.
187.
188.
189.
190.
191-200. Найти частные решения уравнений, удовлетворяющие заданным начальным условиям.
Уравнение
|
191. |
|
|
|
|
192. |
|
|
|
|
193. |
|
|
|
|
194. |
|
|
|
|
195. |
|
|
|
|
196. |
|
|
|
|
197. |
|
|
|
198.
199.
200.
9. Ряды
201-210 Проверить, выполняется ли необходимое условие сходимости ряда..
201.
206.
202.
207.
203.
208.
204.
209.
205.
210.
211-220. Исследовать сходимость числового ряда.
211.
216.
212.
217.
213. 
218.
214. 
219.
215. 
220. 
221-230. Исследовать на абсолютную и условную сходимость
221.
226.
222. 
227.
223.
228.
224.
229.
225. 
230. 
231-240. Найти радиус и интервал сходимости степенного ряда на концах интервала сходимости.
231.
236.
232. 
237.
233.
238.
234. 
239.
235.
240.
241-250. Вычислить приближенно определенный интеграл, используя разложение подинтегральной функции в степенной ряд. Результаты получить с точностью до 0.001.
241.
246.
242.
247.
243.
248.
244.
249.
245.
250.
Элементы линейной алгебры
251-260 Дана система трех линейных уравнений с тремя неизвестными. Требуется найти ее решение с помощью: а) формул Крамера; б) матричного метода Гаусса.
251.
256.
252.
257.
253.
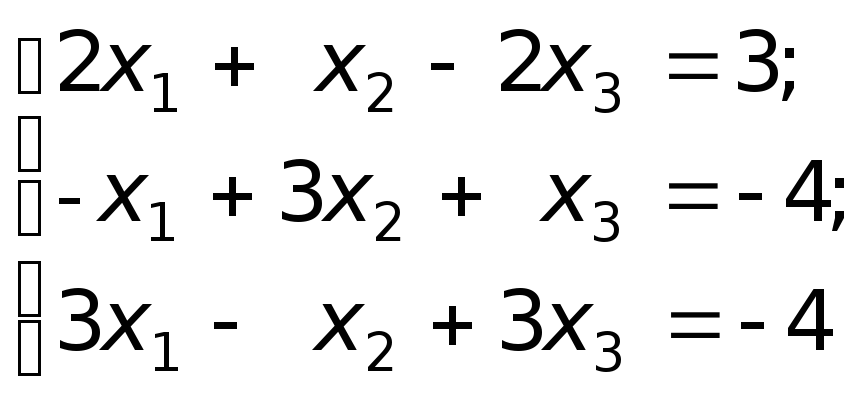258.
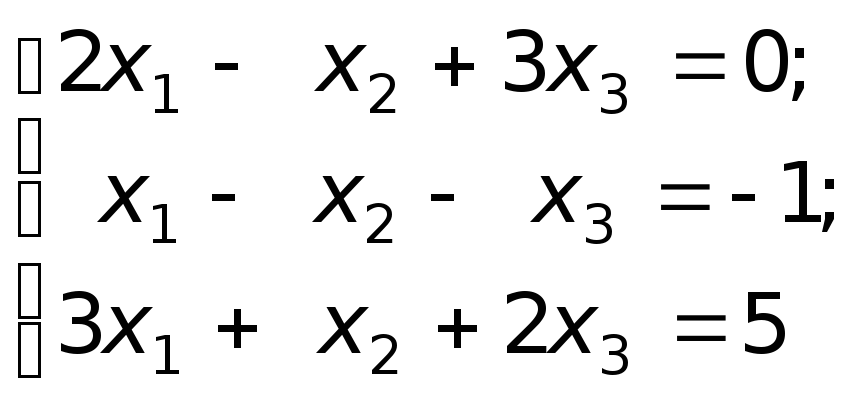
254.
259.
255.
256.
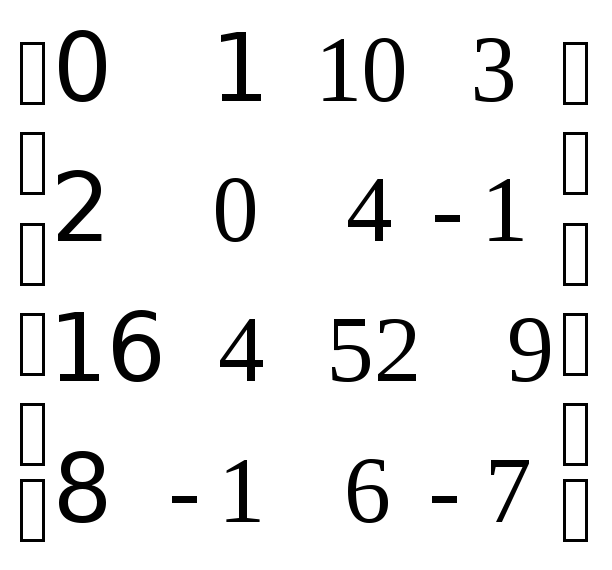
261-270. Найти рнаг матрицы.
261.
266.
262.
267.
263.
268.
264.
269.
265.
270.
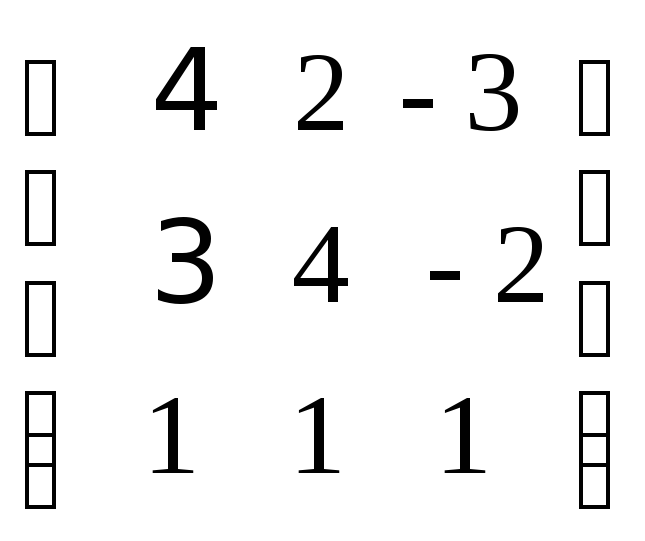
271-280. Проверить, являеттся ли матрица вырожденной, и в случае отрицательного ответа найти обратную матрицу. Выполнить проверку парвильности определения обратной матрицы.
271.
276.
272.
277.
273.
278.
274.
279.
275.
280.
281-290. Исследовать на совместность систему линейных алгебраических уравнений и в случае положительного ответа описать ее совокупность решений.
281.
286.
282.
287.
283.
288.
284.
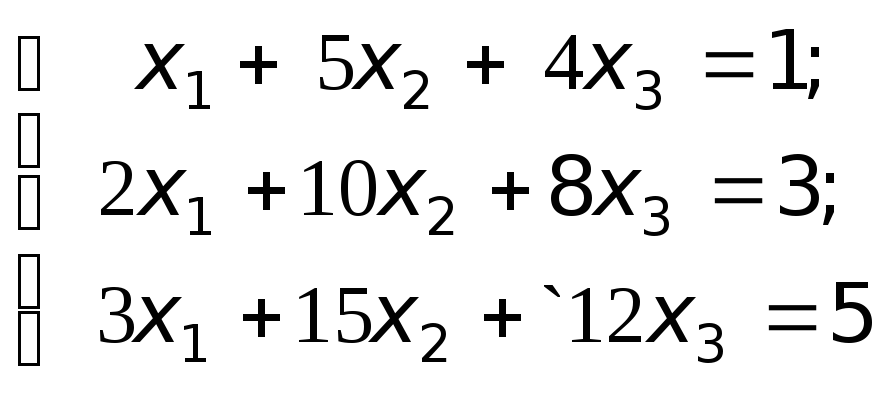289.
285.
290.