
методичка №359
.pdfВВЕДЕНИЕ
Теория автоматического управления (ТАУ) дает основную теоретическую базу для анализа и синтеза автоматических и автоматизированных систем управления и регулирования (АСУ и АСР) вне зависимости от области техники. Выполнение практических работ позволит закрепить и углубить полученные теоретические знания.
Предлагаемый комплекс практических работ охватывает некоторые разделы линейной теории автоматического управления. Все практические работы выполняются на ПЭВМ с использованием современных программных комплексов. Содержанием лабораторных работ является исследование с помощью математических моделей свойств динамических звеньев, их соединений, а также АСУ и АСР, синтез систем с заданными показателями качества.
Перед проведением исследований на ПЭВМ студент должен уяснить суть выполняемой работы, ознакомиться с краткими сведениями из теории, предваряющими каждую работу, выполнить необходимые расчеты, составить схемы, таблицы и т.п. К работе на ПЭВМ студент допускается только при условии выполнения всех этих пунктов индивидуальной (домашней) работы. Это позволит с максимальной эффективностью использовать отведенное на работу машинное время.
Отчет по лабораторной работе должен содержать:
1.Цель работы.
2.Краткие сведения из теории.
3.Исходные данные.
4.Расчеты, графики, структурные схемы с указанием конкретных значений физических величин.
5.Схему модели, составленную из функциональных блоков используемой системы моделирования.
6.Результаты исследований в виде таблиц и графиков с необходимым комментарием.
7.Выводы по работе.
При защите практических работ необходимо знать их содержание и соответствующие разделы теории автоматического управления, дать физическую трактовку результатов исследований.
Моделирование рекомендуется выполнять с использованием современного программного комплекса MATLAB / Simulink.
Simulink позволяет моделировать линейные, нелинейные, дискретные АСУ и их элементы, предоставляет графический интерфейс пользователя для построения
4
модели в виде структурной схемы с использованием мыши. Simulink включает полный комплект библиотек блоков, необходимых для создания модели, устройства отображения и генераторы сигналов и др., позволяет построить иерархические модели. Результаты можно просмотреть во время моделирования на экране, вывести на печать.
Для исследования можно также использовать другие прикладные пакеты (DSM, PDS и т.п.), однако в сравнении с ними Simulink имеет ряд преимуществ.
1. ИССЛЕДОВАНИЕ ТИПОВЫХ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
Цель работы – исследование влияния параметров типовых динамических звеньев на их временные и частотные характеристики.
1 . 1 . Краткие сведения из теории
1.1.1. Общие сведения о динамических характеристиках
В линейной АСР, а также в ее элементах, связь между входной и выходной величинами описывается дифференциальными уравнениями
n d |
n |
y |
n d |
n−1 |
y |
|
dy |
|
m |
d |
m |
x |
m−1 d |
m−1 |
x |
|
dx |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Tn |
|
|
|
+Tn |
|
|
|
+... +T1 |
|
+ y = K |
τm |
|
|
|
+ τm−1 |
|
|
|
+... + τ1 |
|
+ x . (1.1) |
|||
dt |
n |
dt |
n−1 |
dt |
dt |
m |
dt |
m−1 |
dt |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Здесь коэффициенты при производных T1 , T2 , …, Tn и τ1 , τ2 , …, τm имеют размерность времени и называются постоянными времени; коэффициент K, равный отношению выходной величины Y к входной Х в установившемся режиме, имеет размерность: размерность Y / размерность Х и называется коэффициентом усиления при одинаковой размерности Y и Х, и коэффициентом передачи – при разной. Эти коэффициенты зависят от параметров системы (элемента).
В форме, преобразованной по Лапласу при нулевых начальных условиях,
(1.1) имеет вид |
|
|
|
|
+... + τ p +1)x(p), |
|||
(T n pn +T n−1 pn−1 +... +T p +1)y(p)= K(τm pm + τm−1 pm−1 |
||||||||
n |
n−1 |
1 |
m |
m−1 |
1 |
|||
где p = c + jω – комплексная переменная. |
|
|||||||
Передаточная функция системы будет иметь вид |
|
|||||||
|
W (p)= |
y(p) |
K (τm pm + τm−1 pm−1 |
+... + τ p +1) |
|
|||
|
|
= |
m |
m−1 |
1 |
|
(1.2) |
|
|
x(p) |
T n pn +T n−1 pn−1 +... +T p +1 |
|
|||||
|
|
|
|
n |
n−1 |
1 |
|
|
При этом n ≥ m.
Передаточная функция системы определяет статические и динамические свойства системы или ее элементов.
5

Статическая характеристика определяется коэффициентом передачи K.
К динамическим характеристикам относятся временные и частотные характеристики.
Одной из временных характеристик является переходная характеристика – реакция системы (или ее элемента) на единичный скачкообразный сигнал
1(t) |
1 при t > 0; |
= |
|
|
0 при t ≤ 0 . |
Решив (1.2) относительно |
y(t) при условии подачи на вход сигнала |
x(t)=1(t), получим переходную функцию, которую принято обозначать h(t) (в отличие от "кривой разгона" y(t), которую получают при действии на входе скачка произвольной величины). Другой временной характеристикой является весовая или импульсная переходная характеристика – это реакция системы (звена) на дельта-функцию δ(t), называемую также функцией Дирака:
∞ при t = 0 ;
=
0 при t ≠ 0 ,
причем ∞∫δ(t)dt =1.
−∞
( δ(t), как и 1(t) – некая математическая абстракция).
Итак, сигнал на выходе линейного элемента (или АСУ) при подаче на вход единичного импульса δ(t) называется весовой или импульсной переходной функцией. Отметим, что весовая функция системы есть оригинал передаточной функции.
Передаточная, переходная и весовая функции системы однозначно связаны друг с другом: зная одну из них, можно всегда найти другую.
Кроме переходной функции для характеристики динамических свойство системы и ее элементов широко используются частотные характеристики.
Частотные характеристики получаю при рассмотрении вынужденных движений звена (системы), вызванных гармоническим воздействием на входе
X (t)= Aвх sin ωt , где Aвх – амплитуда; ω = 2πTк – угловая частота входных коле-
баний с периодом Т К . Если Aвх = 1, то входное воздействие – единичное гармоническое. По окончании переходного процесса на выходе линейной системы устанавливаются гармонические колебания y(t)= Aвых sin(ωt + ϕ) той же частоты, но с другой амплитудой и сдвинутые по фазе относительно входных колебаний на угол ϕ(ω). Изменение амплитуды и фазовый сдвиг являются функциями частоты и выражают динамические свойства элемента (системы). Если изменять
6

частоту от 0 до ∞ и определять установившиеся амплитуду и фазу выходных колебаний для разных частот, можно получить зависимость от частоты соотношения амплитуд A(ω)= Aвых(ω)Aвх(ω) и сдвига фазы ϕ(ω)= ϕвых(ω)− ϕвх(ω). А(ω) – называют амплитудно-частотной характеристикой (АЧХ), ϕ(ω) – фазовой частотной характеристикой (ФЧХ).
Частотные характеристики можно найти как экспериментально, так и теоретически.
Если в (1.2) подставить p = jω, то получим аналитическое выражение для амплитудно-фазовой характеристики (АФХ).
W (jω)= |
K[τmm (jω)m + τmm−−11(jω)m−1 +... + τ1 jω+1] |
(1.3) |
||||
|
|
|||||
|
T n (jω)n +T n−1 |
(jω)n−1 |
+... +T jω+1 |
|
||
|
n |
n−1 |
|
n |
|
|
W (jω) называют также частотной передаточной функцией. Ее можно предста-
вить в виде
W (jω)=U (ω)+ jV (ω)= A(ω) e jϕ(ω),
где U (ω) и V (ω) соответственно действительная и мнимая части; A(ω) – модуль
частотной функции, ϕ(ω) – фаза частотной функции, причем |
|
||||
A(ω)= |
|
W (jω) |
|
= U 2 (ω)+V 2 (ω); |
(1.4) |
|
|
||||
ϕ(ω)= arctg V (ω). |
(1.5) |
||||
|
|
U (ω) |
|
||
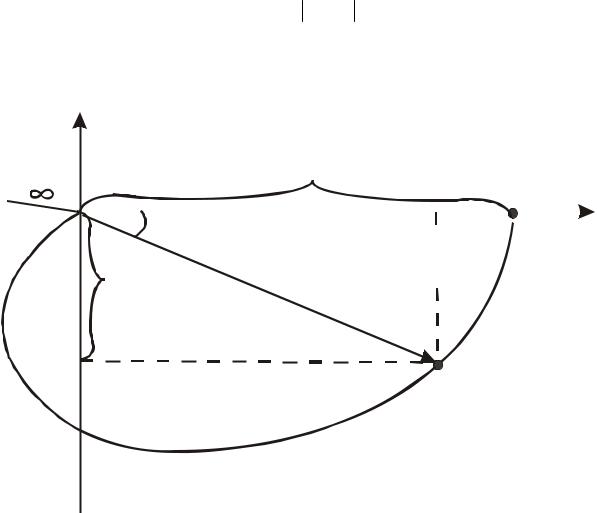
Графически АФЧХ изображается на комплексной плоскости в полярных координатах как годограф функции W (jω), при этом радиус-вектор равен A(ω), а угол поворота ϕ(ω) (см. рис.1.1).
На комплексной плоскости частотную передаточную функцию определяет
→
годограф вектора ОА, длина (модуль) которого равен A(ω), а аргумент (угол, образованный этим вектором с действительной положительной полуосью) ϕ(ω). Кривую, которую описывает конец вектора при изменении частоты от 0 до ∞, называют амплитудно-фазовой частотной характеристикой (АФХ). Таким образом, АФХ – это совмещенная АФХ и ФЧХ.
Можно строить АФХ и в прямоугольных координатах (U (ω), V (ω)), выделив в (1.3) вещественную U (ω) и мнимую V (ω) части.
Заметим, что W (j∞)= 0 . (Свойство передаточной функции).
Часто амплитудную и фазовую частотные характеристики изображают в логарифмическом масштабе.
7
При построении логарифмической амплитудной частотной характеристики (ЛАЧХ) по оси координат откладывают величину
L(ω)= 20lg A(ω)= 20lgW (jω),
единицей измерения которой является децибел. По оси абсцисс откладывается lg ω в декадах. Декада – интервал, соответствующий изменению частоты в 10 раз.
jV(ω) |
|
|
|
|
|
|
ω = 0 |
U(ωi) |
|
|
ω = 0 |
|
|
|
|
|
||||
ϕ(ωi) |
A |
|
|
|
U(ω) |
|
|
|
|
||||
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
i |
|
|
|
|
V(ωi) |
ωi) |
|
|
W(jω) |
||
|
|
ω |
|
|
||
|
|
= |
|
|
|
|
|
|
ω |
|
|
|
|
A |
Рис.1.1. Амплитудно-фазовая характеристика
Фазовая частотная характеристика строится в полулогарифмических координатах. Фаза откладывается по оси ординат в радианах или угловых градусах, а частота – в логарифмическом масштабе.
1.1.2. Типовые динамические звенья
Любую систему можно представить в виде соединения звеньев – условно выделенных преобразователей сигнала направленного действия. Зная модели отдельных звеньев, можно получить модель всей системы.
Типовые динамические звенья описываются уравнениями не выше второго порядка, имеют один вход и один выход и являются элементами направленного действия.
Апериодическое звено первого порядка Дифференциальное уравнение такого звена имеет вид
8

T dydt + y = Kx ,
где Т – постоянная времени, с;
K– коэффициент усиления (передачи). Передаточная функция
W (p)= TpK+1 .
Переходная функция при x(t)=1(t).
h(t)= K 1 −e−Tt .
При x(t)≠1(t) получаем уравнение кривой разгона |
|
|||||||||||
|
|
|
|
|
|
|
− |
|
t |
|
|
|
|
|
|
|
|
−e |
|
|
(1.6) |
||||
y(t)= K x(t) 1 |
T |
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Звенья второго порядка |
|
|||||||||||
Дифференциальные уравнения таких звеньев имеют вид |
|
|||||||||||
T 2 |
d 2 y |
|
+T |
dy |
+ y = Kx , |
|
||||||
|
|
dt |
|
|||||||||
2 dt 2 |
1 |
|
|
|
|
|
|
|
||||
а передаточная функция |
|
|
|
|
|
|
|
|
|
|||
W (p)= |
|
|
K |
|
|
|
. |
|
(1.7) |
|||
T 2 p +T p +1 |
|
|||||||||||
2 |
|
1 |
|
|
|
|
|
|
|
|||
В зависимости от соотношения постоянных времени T1 и T2 звенья второго порядка подразделяются на апериодическое второго порядка и колебательные. В свою очередь колебательные звенья подразделяют на устойчивое колебательное (обычно его называют просто колебательным), консервативное и неус-
тойчивое колебательное. |
|
|
|
|
|
Соотношение T1 и |
T2 |
выражают через коэффициент |
демпфирования |
||
ξ = T1 2T2 . Обозначив T2 |
= T , получим T1 = 2ξT и тогда (1.7) запишется в виде |
||||
|
W (p)= |
K |
|
||
|
|
. |
(1.8) |
||
|
T 2 p2 + 2ξTp +1 |
||||
Переходные процессы в звеньях второго порядка определяются видом кор- |
|||||
ней характеристического уравнения. |
|
||||
Апериодическое звено второго порядка |
|
||||
Если ξ ≥1, т.е. T1 ≥ 2T2 |
в исходной передаточной функции (1.7), то корни |
||||
характеристического уравнения будут вещественными, и передаточную функцию можно преобразовать к виду
9
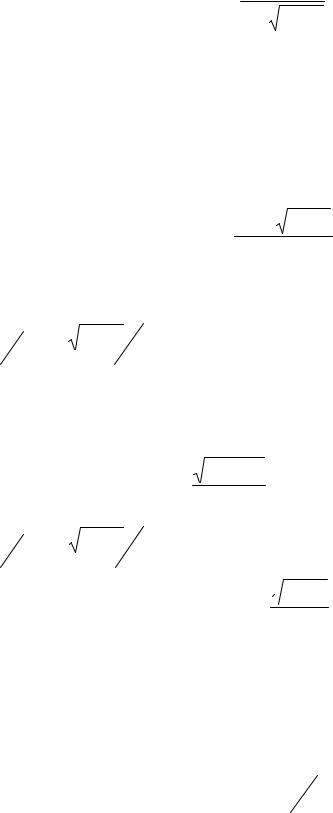
W (p)= |
|
K |
|
|
|
, |
(1.9) |
||
(T p +1)(T p +1) |
||||
3 |
4 |
|
|
|
где |
|
|
|
|
T3,4 = ξ± |
T |
|
||
ξ2 −1 . |
|
|||
Из (1.9) видно, что апериодическое звено второго порядка можно представить как последовательное соединение двух апериодических звеньев первого по-
рядка. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Колебательное звено |
|
|
|||||||
У такого |
звена |
0 < ξ <1; |
корни |
|
характеристического уравнения |
– ком- |
||||||
плексные сопряженные: |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
p |
|
= |
|
−ξ± ξ2 −1 |
; |
|
|
||
|
|
|
1,2 |
|
|
|
|
T |
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p1,2 |
= −α ± jβ, |
|
|
|
||||
где α = ξT , β = |
1−ξ2 |
T . |
|
|
|
|
|
|
|
|
|
|
Переходная характеристика имеет форму затухающих колебаний. |
|
|||||||||||
Решив (1.8) при |
x(t)=1(t) |
и нулевых начальных условиях, найдем пере- |
||||||||||
ходную функцию |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
2 |
+β |
2 |
e−αt sin(βt)+ ϕ0 |
|
|
||
|
h(t)= K 1 |
− |
|
|
, |
(1.10) |
||||||
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где α = ξT ; β = |
1−ξ2 |
T ; |
|
|
|
|
|
|
|
|
|
(1.11) |
ϕ0 = arctg  1 −ξξ2 .
1 −ξξ2 .
Параметры колебательного звена могут быть определены по переходной характеристике (рис.1.2,б).
Передаточный коэффициент K определяют по установившемуся значению h(∞) переходной функции. Постоянную времени Т и коэффициент демпфирования ξ можно найти из соотношений
βT = 2π; |
A1 |
= eαTK , |
K |
|
A3 |
|
|
или
10
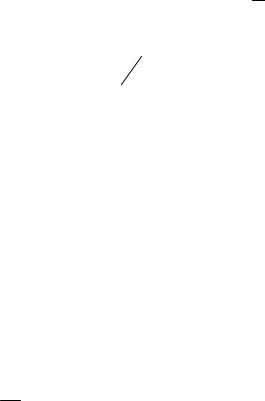
|
β = |
|
2π |
; |
α = |
1 |
|
ln |
A1 |
, |
(1.12) |
|||||
|
T |
|
|
|
|
A |
||||||||||
|
|
K |
|
|
|
|
Т |
К |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
||||
|
|
|
|
|
или α = |
2 |
ln |
|
A1 |
. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
T |
K |
|
A |
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
где TK |
– период колебаний; |
|
|
|
|
|
|
|
|
|
|
|
|
|||
A1 |
и A3 - амплитуды двух соседних колебаний относительно установивше- |
|||||||||||||||
|
гося значения. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Консервативное звено |
|
|
|||||||||
Это звено можно |
считать частным случаем |
колебательного |
звена при |
|||||||||||||
ξ = 0 . Это идеализированное звено, соответствующее колебательному звену, ра-
ботающему без потери энергии. |
|
|
|
|
|
Передаточная функция такого звена |
|
|
|
|
|
W (p)= |
K |
. |
|
|
|
T 2 p2 +1 |
|
|
|
||
Переходная функция |
|
|
|
|
|
h(t)= K(1−cos ω t); |
ω = |
1 |
, |
||
|
|||||
1 |
1 |
T |
|
||
|
|
|
|
||
и характеристическое уравнение имеет вид мнимые корни p1,2 = ± j T1 .
Переходная характеристика – незатухающие колебания постоянной амплитуды, т.е. гармонические колебания с частотой ω = 1T (см. рис.1.2,в).
Неустойчивое колебательное звено При ξ < 0 в звене второго порядка после подачи на его вход единичного
скачка возникают незатухающие расходящиеся колебания, поскольку действительная часть корней оказывается положительной (см. рис.1.2,г).
Интегрирующее звено В таком звене выходной сигнал пропорционален интегралу от входной ве-
личины
y(t)= K ∫t x(t)dt ,
0
или
dydt = Kx ,
а передаточная функция имеет вид
11

Рис 1.2. Переходные процессы в звеньях второго порядка: а – апериодическом второго порядка ( ξ ≥1);
б– колебательном ( 0 < ξ <1);
в– консервативном ( ξ = 0 );
г –неустойчивом колебательном ( ξ < 0 ).
12

W (p)= |
K |
. |
(1.13) |
|
|||
|
p |
|
|
Переходная функция (при x(t)=1(t))
а передаточная функция |
|
|
|
|
|
|
|
||
W (p)= |
|
Kp |
|
. |
(1.15) |
||||
Tp +1 |
|||||||||
|
|
|
|
||||||
Передаточная функция реального звена |
|
|
|||||||
h(t)= |
K |
e− |
t |
|
|
||||
T |
. |
|
|
||||||
|
|
|
|||||||
|
T |
|
|
|
|
|
|
|
|
Пропорциональное звено |
|
||||||||
У такого звена выходная величина пропорциональна входной |
|
||||||||
y = Kx , |
|
|
|
|
|
|
(1.16) |
||
где K – коэффициент передачи, имеющий размерность ед.вых./ед.входа.
(Если размерности x и y одинаковы, то K называют коэффициентом усиления).
Звено запаздывания Такое звено описывается линейным уравнением с запаздывающим аргу-
ментом
y(t)= x(t −τ),
где τ – время запаздывания.
13
