
методичка №359
.pdf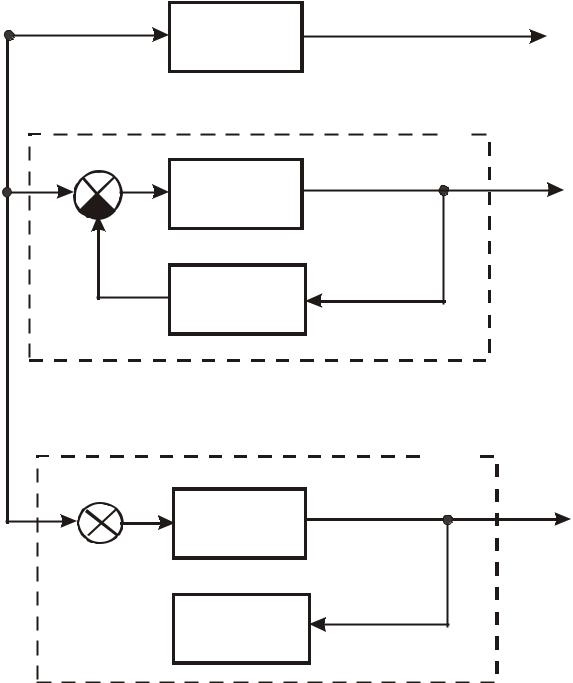
1(t) |
W(p) |
h(t) |
Ф1(p)
W(p) |
1 |
|
h (t) |
Woc(p)
Ф2(p)
W(p)
Woc(p)
Рис.2.2. Схема моделирования звеньев, охваченных обратной связью
2.Как влияет жесткая обратная связь на свойства апериодического и интегрирующего звеньев?
3.В каких случаях целесообразно применение жестких отрицательных (положительных) обратных связей?
4.Как влияет жесткая отрицательная обратная связь на коэффициент усиления соединения?
5.Как влияет жесткая положительная обратная связь на коэффициент усиления соединения?
24
6.Как влияют отрицательная и положительная обратные связи на амплитуду и фазу апериодического и интегрирующего звеньев?
3. АНАЛИЗ УСТОЙЧИВОСТИ АВТОМАТИЧЕСКИХ СИСТЕМ УПРАВЛЕНИЯ И РЕГУЛИРОВАНИЯ
Цель работы – исследование влияния параметров АСР на устойчивость и определение запасов устойчивости по модулю и фазе.
3 . 1 . Краткие сведения из теории
Одним из основных условий работоспособности АСР является ее устойчивость, т.е. способность системы возвращаться в исходное состояние после снятия воздействия, выведшего ее из этого состояния.
Необходимым и достаточным условием устойчивости системы является отрицательность вещественной части комплексных корней характеристического уравнения. Характеристическое уравнение получают обычно приравнивая к нулю дифференциальный оператор при выходной величине в исходном дифференциальном уравнении.
Вычисление корней весьма просто лишь для характеристического уравнения первой и второй степени. Существуют общие выражения для корней уравнений третьей и четвертой степени, но эти выражения громоздки и практически не применяются. Для уравнений более высоких степеней вообще невозможно написать общие выражения для корней через коэффициенты характеристического уравнения.
Существуют правила, позволяющие определять устойчивость системы без вычисления корней. Эти правила называют критериями устойчивости. Существует несколько критериев устойчивости. Все они математически эквивалентны, так как решают вопрос о знаке вещественной части корней характеристического уравнения. Их разделяют на алгебраические и частотные.
Алгебраические критерии позволяют судить об устойчивости системы по коэффициентам характеристического уравнения
а |
n |
pn + a |
n−1 |
pn−1 +... + a p + a |
0 |
= 0 . |
(3.1) |
|
|
1 |
|
|
Во-первых, необходимым (но недостаточным!) условием устойчивости является положительность всех коэффициентов an ,..., a0 характеристического уравнения. Если хотя бы один из коэффициентов меньше нуля, то система не ус-
25
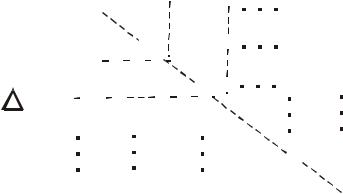
тойчива и дальнейшее исследование не имеет смысла. Если an > 0, an−1 > 0, …, a0 > 0 , то согласно алгебраическому критерию устойчивости Гурвица система устойчива, если все определители Гурвица больше нуля. Для коэффициентов уравнения (3.1) составляют квадратную матрицу n ×n , по главной диагонали которой записывают все коэффициенты от an−1 до a0 и далее заполняют ее, как показано ниже. В случае отсутствия данного коэффициента и если его номер больше n или меньше нуля, на его место проставляют ноль:
|
|
|
ап -1 |
ап -3 |
|
|
ап -5 |
|
0 |
0 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
ап |
|
ап-2 |
|
|
ап -4 |
|
0 |
0 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||
= |
|
|
|
0 |
|
|
ап -1 |
|
|
ап -3 |
|
|
0 |
|
|
|
||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
ап |
|
|
|
|
ап-2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
0 |
|
0 |
|
|
0 |
|
|
|
|
|
а2 |
а-0 |
|
|
|
||||||||
Определители Гурвица составляют так: |
|
|
|
|
||||||||||||||||||||
1 |
= an−1 |
> 0 ; |
|
|
2 |
= |
|
an−1 |
an−3 |
|
> 0 и т.д. |
|||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an |
an−2 |
|
|
|
Последний определитель включает всю матрицу. Но каждый последующий определитель может быть вычислен через предыдущий. Так как в устойчивой сис-
теме |
n−1 > 0 , то положительность последнего определителя обеспечивается, ес- |
ли a0 |
> 0 . |
Для систем невысоких порядков можно не составлять определитель Гурвица. Например, для системы третьего порядка при положительности всех коэффициентов характеристического уравнения условие устойчивости сводится к выполнению неравенства a2a1 > a3a0 .
Критические предельные значения параметров АСР могут быть найдены из условия a2 a1 = a3a0 .
Если характеристическое уравнение имеет невысокий порядок, то применение алгебраических критериев достаточно просто. Если же уравнение имеет высокий порядок, то применять алгебраические уравнения затруднительно. В том случае, когда система включает звено запаздывания, характеристическое уравнение становится трансцендентным из-за члена e− pτ .
В подобных случаях используют частотные критерии. Они удобны в силу простоты геометрической интерпретации и наглядности.
26

Согласно критерию Михайлова для устойчивости системы необходимо и достаточно, чтобы с ростом ω от 0 до ∞ годограф Михайлова, начинаясь на положительной части действительной оси, обходил последовательно п квадрантов, где п – порядок характеристического уравнения
аn pn + an−1 pn−1 +... + a1 p + a0 = 0
На рис.3.1 показаны кривые Михайлова для устойчивых систем различных порядков.
jV(ω)
n = 2 |
n = 1 |
|
n = 3 |
U(ω) |
n = 5
n = 4
Рис.3.1. Кривые Михайлова для устойчивых систем
Для того, чтобы повысить точность статической системы регулирования, т.е. снизить статическую ошибку, необходимо увеличить коэффициент передачи системы. Однако, для существенного уменьшения статического отклонения при этом требуется увеличивать коэффициент передачи до очень больших величин. Технически это реализовать возможно, однако на величину коэффициента усиления накладывается ограничение по условию устойчивости. В связи с этим оп-
27

ределение предельного коэффициента усиления имеет важное практическое значение. Определение предельного коэффициента усиления равносильно определению условия нахождения системы на границе устойчивости.
Для того, чтобы найти предельный коэффициент усиления, необходимо выполнить анализ характеристического уравнения.
Рассмотрим пример. Пусть задано характеристическое уравнение системы
(T1 p +1)(T2 p +1)(T3 p +1)+ k = 0 .
Это уравнение соответствует системе регулирования, содержащей три инерционных звена с общим коэффициентом усиления k . Необходимо определить предельное значение kпр , при котором система перестает быть устойчивой.
Перепишем это уравнение в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
T T T p3 + |
(T T +T T +T T |
)p2 +(T +T +T |
)p +1+ k = 0 , |
|||||||||||||||||||||||||||||
1 |
2 |
3 |
|
1 |
2 |
|
|
1 |
|
|
3 |
|
2 |
3 |
|
1 |
|
2 |
|
3 |
|
|
|
|
||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
3 |
p3 |
+ a |
2 |
p2 |
+ a p + a |
0 |
= 0 . |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Согласно критерию Гурвица система устойчива, если выполняются нера- |
||||||||||||||||||||||||||||||||
венства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
3 |
> 0; |
|
1 |
= a |
2 |
|
|
> 0 ; |
|
|
2 |
= |
|
|
a2 |
a0 |
|
= a |
2 |
a − a |
a |
0 |
> 0 ; |
||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a3 |
a1 |
|
|
|
1 |
3 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
a0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
3 = |
|
a3 |
a1 |
|
|
0 |
= a0 2 > 0 , |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
a2 |
|
|
a0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
т.е. если, при условии положительности всех коэффициентов, выполняется неравенство
a2 a1 > a3 (1+ k ), где (1+ k )= a0 . |
(3.2) |
Неравенство (3.2) можно переписать в виде
k < a2 a1 −1. a3
Это неравенство нарушится при
k ≥ kпр = аа2 а1 −1.
3
Пусть, например, T1 = 0,2 с; T2 = 0,1с; T3 = 0,5с.
Тогда a3 =T1T2T3 = 0,2 0,1 0,5 = 0,01;
a2 = T1T2 +T1T3 +T2T3 = 0,2 0,1+ 0,2 0,5 + 0,1 0,5 = 0,17 ; a1 =T1 +T2 +T3 = 0,2 + 0,1+ 0,5 = 0,8 .
Согласно (3.2)
28
kпр |
= |
0,17 0,8 |
−1 =12,6 . |
|
0,01 |
||||
|
|
|
Теперь применим для решения этой задачи критерий устойчивости Михайлова.
Запишем характеристический полином в виде
А(р)= D(р)+ k ,
где
D(р)= (T1 p +1)(T2 p +1)(T3 p +1).
Для решения задачи следует построить годограф Михайлова
|
|
|
|
|
A(jω)= D(jω)+ k . |
|
|
|
|
|
|||||
|
Построим вначале годограф |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
D(jω)= (T1 jω+1)(T2 jω+1)(T3 jω+1) |
|
|
(3.3) |
||||||||
Преобразуем (3.3) к виду D(jω)=U (ω)+ jV (ω), где |
|
|
|
|
|
||||||||||
|
|
|
|
U (ω)=1− a2ω2 ; |
|
|
|
|
|
|
|||||
|
|
|
|
V (ω)= ω(a − a |
ω2 ). |
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
Подставив значения ai |
из предыдущего примера, получим |
|
|
|||||||||||
|
|
|
|
U (ω)=1−0,17ω |
2 |
; |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
(3.4) |
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V (ω)= ω(0,8 −0,01ω ) |
|
|
|
|
|
||||||
|
Задаваясь значениями ω в диапазоне от 0 до ∞, рассчитываем значения |
||||||||||||||
U (ω) и V (ω). Результаты расчета сводим в табл.3.1. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ω, с-1 |
|
0 |
1,0 |
2,0 |
3,0 |
4,0 |
|
5,0 |
6,0 |
|
8,94 |
20,0 |
∞ |
||
U (ω) |
|
1 |
0,83 |
0,32 |
-0,53 |
-1,72 |
-3,25 |
-5,12 |
-12,6 |
-67 |
−∞ |
||||
|
|
0 |
0,79 |
1,52 |
2,13 |
2,56 |
2,75 |
2,64 |
|
0 |
-64 |
|
|||
V (ω) |
|
|
−∞ |
||||||||||||
|
При частоте ω = 8,94, как следует из (3.4), V (ω)= 0 , т.е. годограф пересе- |
||||||||||||||
кает действительную ось. |
|
|
|
|
|
|
|
|
|
|
|
||||
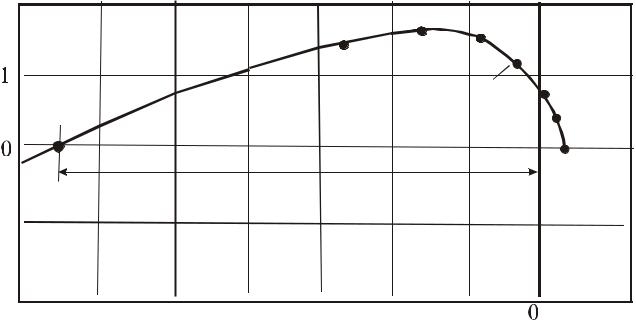
|
Годограф D(jω) показан на рис.3.2. |
|
A(jω), достаточно мнимую ось сме- |
||||||||||||
|
Для того, чтобы получить годограф |
||||||||||||||
стить влево на величину k . Из рис.3.2 следует, что система находится на границе
устойчивости, если значение k равно значению kпр , при котором |
годограф |
A(jω) пройдет через начало координат. Согласно рис.3.2 величина |
kпр =12,6 , |
что совпадает с результатом предыдущей задачи. |
|
29
jV(ω) |
|
|
|
|
|
|
|
|
|
|
=8,94 |
|
|
|
ω=6,0 |
ω=5,0 |
ω=4,0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
2 |
|
|
пр |
|
|
|
|
|
ω=3,0 |
= |
|
,0 |
|
|
|
|
|
|
ω |
|
|
|||
|
|
|
|
|
|
|
|
|
1 |
|
ω=ω |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
ω |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kпр |
|
|
ω=0 |
|
||
-1 |
|
|
|
|
|
|
|
|
|
|
-14 |
-12 |
-10 |
-8 |
-6 |
-4 |
-2 |
|
U(ω) |
||
|
|
|
|
|
|
|
|
|||
|
Рис.3.2. К определению предельного коэффициента с использованием |
|||||||||
|
|
критерия устойчивости Михайлова |
|
|
|
|
|
|||
Удобным критерием устойчивости является критерий Найквиста, основанный на анализе частотных характеристик разомкнутой системы. АФХ разомкнутой системы можно получить как аналитически, так и экспериментально. Это обстоятельство выгодно отличает этот критерий от рассмотренных ранее.
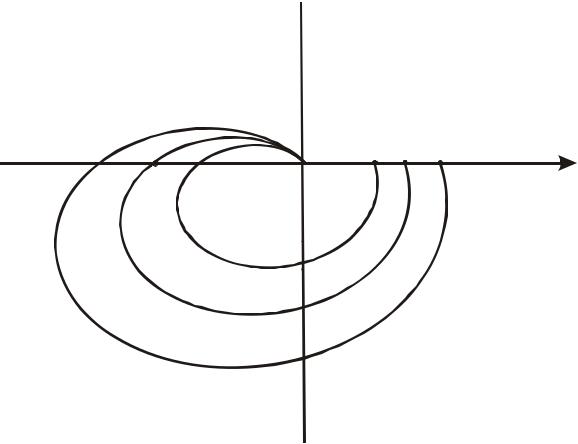
В простейшем случае (система устойчива в разомкнутом состоянии) формулировка критерия Найквиста такова: для устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы W (jω) при изменении частоты ω от 0 до ∞ не охватывала точку (−1, j0). На рис.3.3 показаны частотные годографы для разных значений коэффициента передачи системы. При k < kкр годограф не охватывает критическую точку (кривая 1) и система является устойчивой. При k > kкр годограф охватывает критическую точку (кривая 2) и
система при таком коэффициенте передачи становится неустойчивой. При k = kкр система оказывается на границе устойчивости (кривая 3).
Частотные годографы разомкнутой системы при разных значениях коэффициента передачи.
Пусть, например, передаточная функция разомкнутой системы
W (p)= |
|
|
K |
|
(T p +1)(T p +1)(T p +1) |
|
|||
1 |
2 |
3 |
|
|
30
и требуется определить критический коэффициент передачи (заметим, что эта передаточная функция соответствует в рассмотренном выше примере характеристическому полиному замкнутой системы).
 jV(ω)
jV(ω)
U(ω)
1
2
3
Рис.3.3. Частотные годографы разомкнутой системы при разных значениях коэффициента передачи: 1 – k < kкр ; 2 – k = kкр ;
3 – k > kкр
Условию прохождения годографом точки (−1, j0) при k = kкр соответствует уравнение
|
|
|
W (jωπ )= −1, |
|
|
|
|||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
kкp |
|
|
|
= −1, |
|
|
(T jω |
π |
+1)(T jω |
π |
+1)(T jω |
π |
+1) |
||
1 |
2 |
|
3 |
|
|
||||
откуда
(T1 jωπ +1)(T2 jωπ +1)(T3 jωπ +1)+ kкp = 0 .
Составим уравнения частей:
(T T |
+T T |
+T T |
)ω2 |
+ k |
кp |
+1 = 0 |
(3.5) |
1 2 |
1 3 |
2 3 |
π |
|
|
|
31

|
|
|
ω(T +T +T −T T T ω2 )= 0 |
(3.6) |
||||||||||||||||||
|
|
|
|
|
1 |
|
2 |
|
3 |
|
|
1 |
2 |
3 |
π |
|
||||||
Из (3.6) |
ωπ2 = |
T1 +T2 +T3 |
. После подстановки в (3.5) |
|
||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
T1T2T3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
+T2 +T3 )−1. |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ T |
|
|
|
|||||
|
|
|
k р.кp = T + T |
|
|
|
(T1 |
|
||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
3 |
|
|
|
|
|||||
Взяв те же числовые значения параметров, что и в предыдущих примерах, |
||||||||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
k р.кp. |
= |
|
+ |
|
|
|
+ |
|
|
|
|
(0,2 + 0,1 + 0,5)−1 =12,6 . |
|
|||||||
|
|
0,2 |
0,1 |
0,5 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Т.о., результаты совпадают.
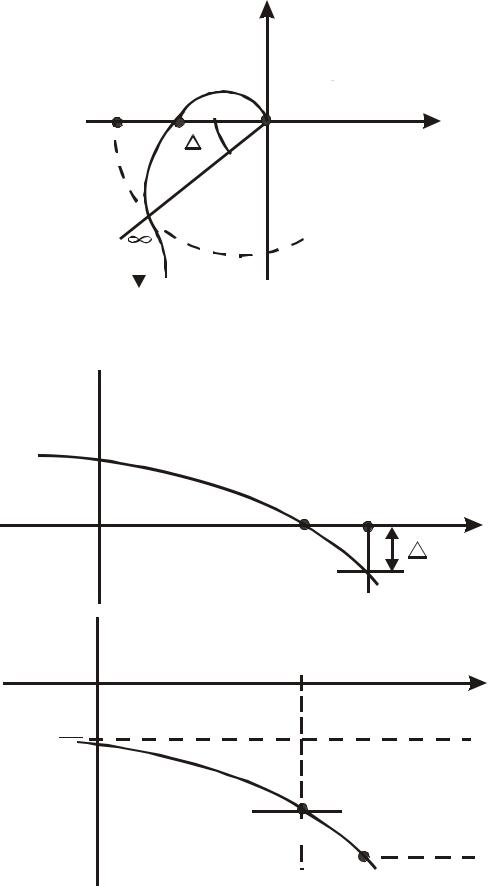
Для определения запасов устойчивости системы можно воспользоваться
АФХ или ЛЧХ разомкнутой системы. Запасы устойчивости характеризуют удаление частотного годографа разомкнутой системы от критической точки
(−1, j0).
Запас устойчивости по фазе ϕ (рис.3.4, а) измеряется по дуге окружности единичного радиуса с центром в начале координат между точкой (−1, j0) и точ-
кой, соответствующей частоте среза ωср , где ω(jωcp )=1.
Запас устойчивости по модулю определяется отрезком ОА, отсекаемым
годографом на отрицательной действительной полуоси, где ωπ – частота в точке
пересечения. Определение запаса устойчивости по ЛЧХ показано на рис.3.4, б.
3 . 2 . Программа выполнения работы
В данной работе предлагается выполнить анализ устойчивости или опре-
делить критические значения параметров ряда систем из условия устойчивости.
3.2.1. Исследование устойчивости АСУ приводом летучих ножниц
1. По функциональной схеме АСУ приводом барабана летучих ножниц
(рис.3.5) составить структурною схему.
Двигатель совместно с системой управления описывается дифференциаль-
ным уравнением
T 2 |
d 2ω |
|
+T |
dω |
+ ω = kU , |
|
|
dt |
|
||||
2 dt 2 |
1 |
|
||||
где ω – частота вращения, рад/с; |
|
|
|
|
||
T1, T2 – постоянные времени, с; |
|
|
|
|
||
32
-1 |
ωπ |
0 |
A |
ϕ |
U(ω) |
ωcp 
ω 
0
а)
 L(ω), дБ
L(ω), дБ
ωcp ωπ |
-1 |
|
ω, c |
|
L |
 ϕ(ω), рад
ϕ(ω), рад
ωcp ω, c-1
- π2
-π 





 ϕ
ϕ


 ωπ
ωπ
б)
Рис.3.4. К определению запасов устойчивости
33
