5. Приклади афінних перетворень

Приклад 1. Повернути трикутник АВС з координатами (3;-1), (4;1), (2;1) на 90^о проти часової стрілки відносно початку координат.

Використовуючи матрицю координат 3х2 та формули повороту отримаємо:

.

Рис. 6 Поворот трикутника АВС в

Приклад 2. Відобразити трикутник DEF з координатами (8;1), (7;3), (6;2) спочатку відносно осі Y=0 у трикутник , а потім відносно прямоїx=y у трикутник .

Відображення відносно осі Y=0:

.

Відображення відносно прямої x=y:

.

Рис. 7 Відображення трикутника DEF

Приклад 3.

Нехай задано трикутник ABC з координатами (2;2), (4;2), (4;4). Знайти координати нового трикутника, повернутого на 90^о відносно початку координат та відображеного відносно прямої y=-x.

Перша матриця повороту має вигляд:

Матриця відображення відносно y=-x відповідно рівна:

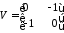
Результатом повороту та відображення координат K трикутника ABC будуть координати K^*:

,

.

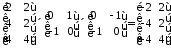Якщо провести перетворення в оберненому порядку (спочатку відображення, а потім поворот), то отримаємо трикутник :

.

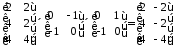Рис. 8 Комбінований поворот та відображення трикутника ABC (– проміжний трикутник прямої задачі,– проміжний трикутник оберненої задачі)

Приклад 4. Побудувати матрицю повороту точки M(x, y) відносно довільної точки N(m, n) на кут ϕ у додатному напрямку.

Однорідні координати дають можливість знайти матрицю повороту відносно довільної точки. У загальному випадку поворот відносно довільної точки може бути реалізований шляхом таких перетворень:

1. переміщення точки N(m, n) на вектор (–m, –n) так, щоб центр повороту сумістився з початком координат. Матриця цього перетворення має вигляд:

2. поворот точки на кут ϕ у додатному напрямку відносно початку координат. Матриця цього перетворення визначається формулою:

Отже, для знаходження результуючого повороту точки M(x, y) відносно точки N(m, n) потрібно перемножити задані матриці за вказаним порядком:

[X,Y,1] =[x,y,1] .

Приклад 5. Нехай задано рівняння прямої L та трикутник ABC з координатами вершин (2,4,1), (4,6,1), (2,6,1). Дзеркально відобразити трикутник відносно даної прямої.

Пряма L пройде через початок координат під час зсуву її на 2 одиниці по осі ОY (матриця зсуву матиме вигляд – ). В результаті повороту навколо початку координат напряма співпаде з віссюОХ (матриця повороту матиме вигляд – ). Далі необхідно дзеркально відобразити об’єкт за допомогою матриці дзеркального відображенняі повернутись в початкову орієнтацію. Комбінація перетворень матиме вигляд:

=.

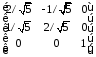
Отже, координати нового трикутника матимуть будуть такими:

=.

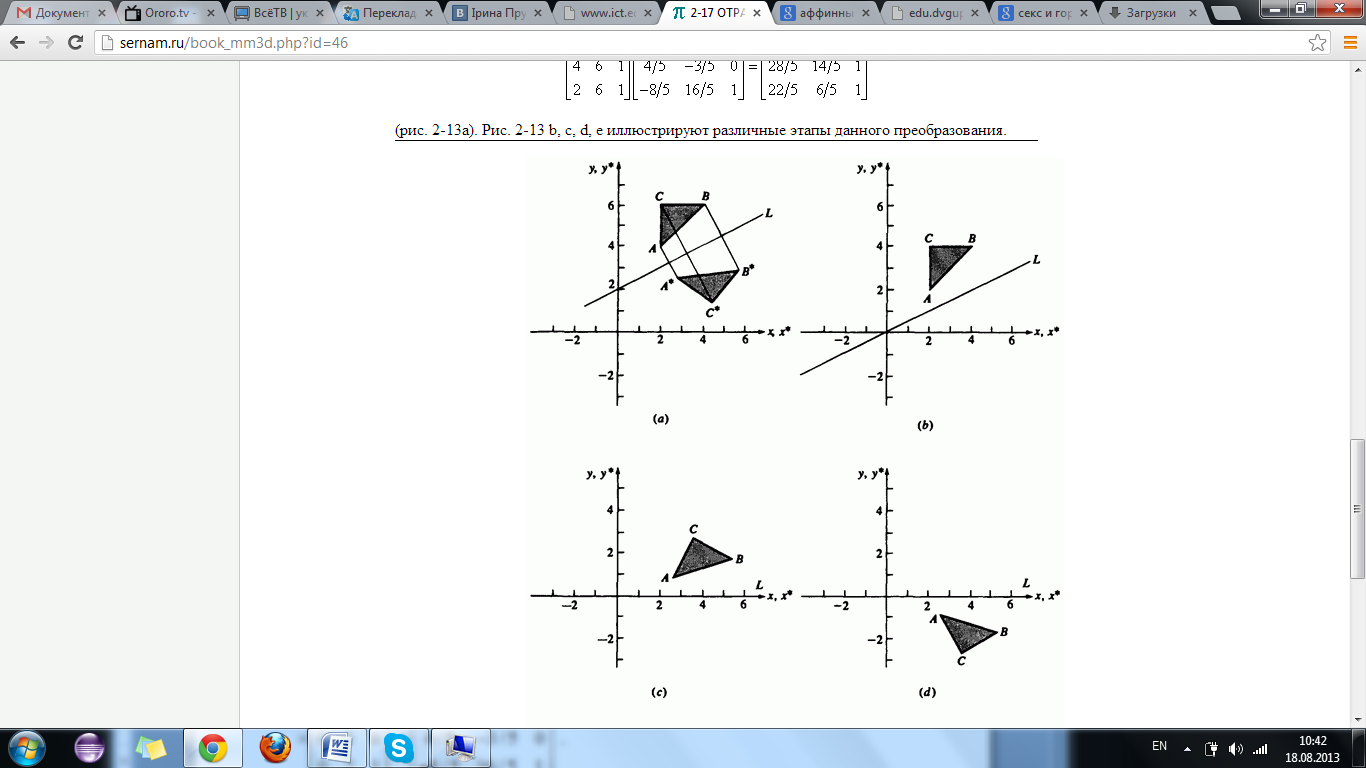
а) б)

в) г)

д)

Рис 9. Відображення відносно будь-якої кривої а)початкове та кінцеве положення трикутника; б)зсув прямої в початок координат; в)поворот прямої та її спів падіння з віссю ОХ; г) відображення відносно осі ОХ; д) обернений поворот.

Висновки

Ідея опису точки вектором виникла з геометричних уявлень. Теореми геометрії розвивалися для афінної геометрії з часом. У них важливими є поняття паралельності і співвідношення між паралельними прямими.

Афінне перетворення є комбінацією лінійних перетворень, супроводжуваних переносом зображень. Афінні перетворення формують зручну підсистему білінійних перетворень, тому що добуток двох афінних перетворень також є афінним. Це дозволяє представити узагальнену орієнтацію системи точок стосовно довільної координатної системи при збереженні одиничного значення однорідної координати h.

Отже, афінні перетворення найбільш часто використовуються в комп'ютерній графіці. І як було показано, вони значно спрощують масштабування, поворот і зсув зображень.