Крива Без’є

Вперше криві були представлені широкій публіці в 1962 році французьким інженером П'єром Без'є, який, розробивши незалежно від де Кастельє, використовував їх для комп'ютерного проектування автомобільних кузовів. Криві були названі ім'ям Без’є, а ім'ям де Кастельє названо розроблений ним рекурсивний спосіб визначення кривих (алгоритм де Кастельє).

Згодом це відкриття стало одним з найважливіших інструментів систем автоматизованого проектування та програм комп'ютерної графіки.

Крива Без’є – основа векторної графіки. Застосування кривої Беє’є є досить широким: спосіб управління рухом, засіб створення анімаційних рисунків, метод опису художніх шрифтів, спосіб передачі виділених об’єктів, інтерактивний інструмент дизайну форми різноманітних об’єктів.

У багатьох методах побудови тривимірних кривих отримувана крива проходить через всі задані точки, тобто ці методи є методами інтерполяції. В багатьох випадках вони дозволяють отримати добрі результати. Але ці методи мають ряд недоліків, що роблять їх малопридатними для систем побудови кривих в діалоговому режимі. Це пояснюється тим, що задання форми кривої з допомогою таких числових характеристик, як напрямок і модуль дотичних векторів, не забезпечує інтуїтивного відчуття правильності побудови кривої, тобто не завжди існує очевидний зв’язок між числами і формою кривої. Крім того, методи підгонки тривимірними кривими в результаті дають криву одного і того самого порядку, який не змінюється. Для того, щоб збільшити кривизну, потрібно вводити більшу кількість точок.

Без’є розробив інший метод зображення кривої, який створює у користувача більш природнє сприйняття. Крива Без’є визначається вершинами багатокутника, який задає форму кривої. Кривій належить перша та остання вершина, в той час як інші вершини характеризують похідні, порядок та вид кривої. Таким чином, крива задається з допомогою відкритого багатокутника (ламаної) сформованого заданими точками, як показано на рис 1.

Рис 1. Приклади кривих Без’є

Так як вигляд кривої залежить від форми багатокутника, то зміна положення вершин цього багатокутника створює у користувача значно більше явного відчуття сприймання зв’язку між входом і виходом. Для того щоб збільшити порядок будь-якого криволінійного сегменту, потрібно тільки задати додаткові вершини. Така методика відрізняється значною гнучкістю і позбавлена багатьох недоліків підгонки кубічними сплайнами і параболічної інтерполяцїї.

Крива Без’є – параметрична крива, що задається виразом:

.

n – степінь полінома, який характеризується n+1 вершинами,

i – порядковий номер вершини,

–функція компонент векторів опорних вершин,

–базисні функції кривої Без'є, названі також поліномами Бернштейна.

,

.

Точки Р0, Рn називаються кінцевими, а точки Р1,...,Рn-1 контрольними,

Ламана P0P1 … Pn називається контрольною (опорною).

Властивості многочленів Бернштейна суттєво впливають на поведінку кривих Без’є. Наведемо деякі з них:

1. Многочлени Бернштейна набувають невід’ємних значень.

2. В сумі вони дають одиницю.

3. Не залежать від вершин масиву P, а залежать лише від кількості точок у масиві.

Приклад 1. Чотири опорні точки P₀, P₁, P₂ і P₃, задані в 2-вимірному просторі визначають форму кривої.

Лінія бере початок з точки P₀ прямуючи до P₁ і закінчується в точці P₃, підходячи до неї з боку P₂. Тобто крива не проходить через точки P₁ і P₂, вони використовуються для вказівки її напрямків. Довжина відрізка між P₀ і P₁ визначає, як швидко крива поверне до P₃.

Рис.2. Крива Без’є третього степеня

У матричній формі кубічна крива Без’є записується таким чином:

.

Також існує рекурсивна формула побудови кривих Без'є:

У процесі інтерактивного конструювання ламана Без’є є засобом управління формою. Ефективність методу обумовлена такими властивостями кривих Без’є:

1. Порядок точок у масиві Р суттєво впливає на вигляд кривої Без’є.

2. Форма кривої Без’є повторює хід ламаної P₀P₁…P_n. При зміні порядку точок повністю змінюється форма кривої.

Рис.3 Кубічні криві Без’є при зміні порядку точок

3. Перша та остання точки кривої збігаються з відповідними точками масиву P, тобто B(0) = P0, B(1) = Pn. Всі інші вершини ламаної в загальному випадку знаходяться поза кривою.

4. Нахил дотичних векторів в крайніх точках кривої співпадає з нахилом, відповідно першої та останньої ланки ламаної Без’є.

5. У рівнянні, що описує елементарну криву Без’є, немає вільних параметрів, тобто заданий масив однозначно визначає криву Без’є. Тому немає можливостей якимось чином впливати на форму кривої Без’є.

6. Крива Без’є інваріантна відносно афінних перетворень. Тобто побудувавши криву Без’є, над нею можна здійснити афінні перетворення, а можна вчинити інакше: спочатку здійснити афінні перетворення над опорними вершинами, а потім побудувати криву Без’є на нових вершинах. Якщо результати будуть однаковими, то кажуть, що крива є інваріантною відносно цього афінного перетворення. При цьому легко помітити, наприклад, що поворот опорних вершин і подальша побудова кривої займає менше часу, ніж поворот самої кривої. Нагадаємо, що афінні перетворення включають у себе поворот, розтягування/стиск, паралельне перенесення та їх можливі комбінації.

7. Крива Без’є лежить в опуклій оболонці вершин масиву P.

Змістовно многочлен Без’є можна представити як деяку намагнічену еластичну стрічку, закріплену в першій і останній точках. Стрічка притягується до кожної точки, причому чим вище напруженність магнітного поля в точках, тим ближче буде притягнута до них. При прямуванні кратності до нескінченості многочлен Без’є прямує до ламаної кривої, точками спряження для якої служать точки орієнтири.

Практичне конструювання кривих за методом Без’є є евристичною процедурою. Спочатку конструктор вручну накидує бажану криву. Пізніше він вказує вершини ламаної Без’є, яка на його думку, створить перше наближення до необхідної кривої. Наступним кроком є пересування вершин таким чином, щоб поступово покращити співпадання чи наближення. Якщо необхідно, деякі вершини викидаються або додаються нові.

Поряд з перевагами, криві Без’є мають і ряд недоліків :

1. Степінь функціональних поліномів напряму залежить від кількості точок у заданому векторі. Степінь многочлена B(t), що визначає криву Без’є, на одиницю менший від кількості точок масиву, тобто крива Без’є побудована на n+1 точці задається многочленом степеня n.

2. Якщо в масив P додати хоча б одну вершину, то необхідно повністю перерахувати параметричні рівняння кривої Без’є

3. Зміна хоча б однієї точки в масиві P приводить до помітної зміни всієї кривої Без’є.

Незважаючи на недоліки, крива Без’є є зручною до використання в задачах комп’ютерної графіки, оскільки формула є достатньо простою з точки зору математичних обчислень, універсальною з точки зору програмування, геометрично наглядною з точки зору користувача – художника, дизайнера, проектувальника.

Приклад 2. Побудова кривої Без’є.

Р₀=[1,1],

Р₁=[2,3],

Р₂=[4,3],

P₃=[3,1] є вершини багатокутника.

Використаємо формули

де ,

.

Рис. 3. Крива Без’є (приклад 2).

X

Тут n=3, поскільки маємо 4 вершини. Звідси

,

,

,

.

, .

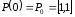Таким чином

Коефіцієнти для кривої Без’є:

t	I3,0	I3,1	I3,2	I3,3
0	1	0	0	0
0.15	0.614	0.325	0.0574	0.0034
0.35	0.275	0.444	0.239	0.043
0.5	0.125	0.375	0.375	0.125
0.65	0.043	0.239	0.444	0.275
0.85	0.0034	0.0574	0.325	0.614
1	0	0	0	1

Складена кубічна крива Без’є – це неперервна крива γ, що є об’єднанням елементарних кубічних кривих γ₀, γ₁, …, γ_l , тобто

.

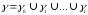Для побудови складеної кривої Без’є розбиваємо масив точок P0, P1,…, Pn (n має бути кратним 3) на l підмножин, кожна з яких містить чотири точки так, що остання точка попередньої підмножини – це перша точка наступної підмножини, тобто

{P0, P1, P2, P3}, {P3, P4, P5, P6}, …, {P3l, P3l + 1, P3l + 2, P3l + 3}.

На кожній такій підмножині можна побудувати елементарну криву Без’є, тобто окремий фрагмент складеної кривої Без’є. Об’єднання окремих фрагментів дає складену кубічну криву Без’є, яка належить до класу неперервних функцій. Якщо тепер змінити якусь точку масиву, то складена крива Без’є зміниться тільки локально. Щоб крива була гладкою, необхідно забезпечити виконання умови на краях двох сусідніх сегментів:

- похідна першого сегменту в останній точці;

- похідна другого (сусіднього) сегменту в першій точці;

g – деяка стала.

Приклад 3. Нехай задано точки P0, P1, P2, P3, P4, P5.

Рис. 4 Вхідні дані для побудови кривої Без’є

Побудуємо криву третього порядку. Як бачимо, з набору точок можна розглянути дві криві (два сегменти) з точками B_i та C_i. Виберемо мередину выдрызка B_n =C₀, що знаходиться між точками P2, P3. Тоді перша крива буде мати: B₀ =Р₀, B₁ =Р₁, B₂ =Р₂, B₃ =С₀, друга крива – С₀ =В₃, С₁ =Р₃, С₂ =Р₄, С₃ =Р₅ (рис.5).

Рис.5. Побудова кривої Без’є

З прикладу випливає, що

,

.

Тобто умова гладкості виконується

тобто

Примітка. Для того, щоб складена кубічна крива Без’є була C1-гладкою необхідно, щоб трійки вершин P3i – 1, P3i , P3i + 1 лежали на одній прямій. Тобто розбиваємо масив точок P₀, P₁,…, P_n на l підмножин таким чином:

{P0, P1, P2, P3}, {P1, P2, P3, P4}, …, {P3l, P3l + 1, P3l + 2, P3l + 3}.

Відрізок {P0, P1, P2, P3}, описує криву між точками P1 та P2, а відрізок {P1, P2, P3, P4} між точками P2 та P3 і т.д. Гладкість зшивання відрізків буде залежати від порядку полінома(чим вищий порядок, тим гладше будуть зшиватись відрізки). На границях необхідно вибрати умову, наприклад, що відповідні похідні рівні нулю.

Зауваження. Метод побудови кривої Без’є в графічних пакетах базується на використанні дотичних управляючих ліній, що проведені до сегмента кривої на його кінцях (вузлах). При цьому форму кривої Без’є моделюють шляхом зміни нахилу дотичних і довжини відрізка, які визначаються контрольними точками.

Завдання

1. Створити редактор кривих Без’є, який дозволяє відобразити криву Без’є за традиційними формулами, передбачає введення і редагування вершин характеристичних багатокутників кривих Без’є через діалогове вікно; відображення кривої Без’є у матричному вигляді.

2. Створити редактор кривої Без’є, який дозволяє відобразити криву Без’є за традиційними формулами, введення і редагування вершин характеристичних багатокутників кривих Без’є через маніпулятор миші; візуалізацію характеристичного багатокутника.

3. Створити редактор кривої Без’є, який дозволяє відобразити криву Без’є за рекурсивними формулами, введення і редагування характеристичних багатокутників кривих Без’є через діалогове вікно; обчислення значень точок, що належать кривій Без’є, заданої кількості.

4. Створити редактор кривої Без’є, який дозволяє відобразити криву Без’є за традиційними формулами, введення і редагування вершин характеристичних багатокутників кривих Без’є через маніпулятор миші; відображення кривої Без’є у параметричному вигляді.

5. Створити навчальну програму, що відображає послідовні кроки побудови кривих Без’є з поясненнями. Вхідні точки задаються/відмічаються в області відображення. Для обчислень точок кривої використати рекурсивну формулу.

6. Створити редактор кривої Без’є, який дозволяє відобразити криву Без’є за рекурсивними формулами, введення і редагування вершин характеристичних багатокутників кривих Без’є через маніпулятор миші; відображення кривої Без’є у матричному вигляді.

7. Створити навчальну програму, що відображає послідовні кроки побудови кривих Без’є з поясненнями. Вхідними даними є числові значення для вершин характеристичного багатокутника, які задаються через діалогове вікно. Для обчислень точок кривої використати традиційну формулу.

8. Створити редактор кривої Без’є, який дозволяє відобразити криву Без’є за традиційними формулами, введення і редагування характеристичних багатокутників кривих Без’є через діалогове вікно; зміну кривизни кривої Без’є.

9. Створити редактор кривої Без’є, який дозволяє відобразити криву Без’є за рекурсивними формулами, введення і редагування вершин характеристичних багатокутників кривих Без’є через діалогове вікно; відображення кривої Без’є у параметричному вигляді.

10. Створити навчальну програму «Побудова кривих Без’є» Вхідними даними є числові значення для вершин характеристичного багатокутника, які задаються через діалогове вікно. Для обчислень точок кривої використати два варіанти формули (традиційну і рекурсивну).

11.Створити навчальну програму «Побудова кривих Без’є». Вхідними даними є числові значення для вершин характеристичного багатокутника, які задаються через діалогове вікно. Для обчислень точок кривої використати традиційну формулу. Відобразити параметричний вид кривої.

Примітка.

Редактор містить довідкову інформацію, підказки, примітки та засоби для налагодження інтерфейсу користувача, контролює коректність введених даних.

Навчальна програма містить теоретичні матеріали, які демонструються на прикладах, підказки, відповідні повідомлення.

Звіт до лабораторної роботи містить усі стандартні компоненти: титульний аркуш, тема, мета, теоретичні відомості, завдання, текст програми з коментарями, результати роботи програми. У теоретичних матеріалах потрібно записати хід обчислення трьох точок кривої Без’є, яка задається характеристичним багатокутником згідно індивідуального варіанту.

Питання для самоперевірки (підготовка до контрольної роботи)

1. Що таке сплайн?

2. У якій задачі вперше використано апарат кривих Без’є?

3. Яким значенням параметру відповідають початкова та кінцева опорні точки? Доведіть це.

4. Чому крива Без’є вважається зручною для використання в задачах комп’ютерної графіки?

5. Чим визначається степінь кривої Без’є?

6. Як змінюється параметр у формулі кривої Без’є?

7. Назвіть недоліки кривих Без’є.

8. Запишіть рекурсивну формулу кривої Без’є.

9. Назвіть корисні властивості кривої Без’є.

10. Чи можна переставити місцями опорні точки без зміни вигляду кривої Без’є?

11. Що таке характеристичний багатокутник кривої Без’є?

12. Запишіть параметричний вигляд кривої Без’є.

МІНІСТЕРСТВО ОСВІТИ І НАУКИ

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ „ЛЬВІВСЬКА ПОЛІТЕХНІКА”