
- •С.Г.Савчук
- •Передмова
- •Передмова до другого видання
- •Список літератури
- •1.2. Математичні та фізичні моделі Землі.
- •1.3. Системи координат, що застосовуються у вищій геодезіі.
- •1.4. Основи теорії поверхонь.
- •Розділ 2 геометрія земного еліпсоїда
- •Таблиця 2.1
- •2.3.1. Зв'язок між геодезичною, приведеною і геоцентричною широтами.
- •2.3.2. Зв’язки між різними видами координат.
- •З використанням введених позначень, формулу (1.8) із розділу 1, запишемо у виді
- •Рис 2.8
- •На основі (2.60) отримаємо
- •Розділ 3 розв’язування геодезичних задач
- •3.1. Види геодезичних задач.
- •3.2. Короткі історичні відомості.
- •3.4.1. Розв’язування сфероїдних трикутників.
- •Сферичний надлишок
- •Таблиця 3.1
- •Способи розв’язування малих сфероїдних трикутників а) за формулами сферичної тригонометрії
- •Б) за теоремою Лежандра
- •Згідно теореми Лежандра, значення кутів плоского (лежандрового) трикутника буде
- •В) за способом аддитаментів
- •Позначивши
- •Г) за виміряними сторонами
- •3.4.2. Розв’язування головних геодезичних задач а) на поверхні сфери
- •Б) на поверхні еліпсоїда
- •В) в просторі
- •3.5. Диференційні формули.
- •3.5.1. Диференційні формули для геодезичної лінії.
- •3.5.2. Диференційні формули для довільної точки простору.
- •3.5.3. Диференційні формули для системи геодезичних координат.
- •3.5. Диференційні формули.
- •3.5.1. Диференційні формули для геодезичної лінії.
- •3.5.2. Диференційні формули для довільної точки простору.
- •3.5.3. Диференційні формули для системи геодезичних координат.
- •3.7.1.Алгоритм та числовий приклад розв'язування прямої і оберненої геодезичних задач на поверхні сфери.
- •Обернена геодезична задача
- •Обернена геодезична задача
- •3.7.5. Алгоритм та числовий приклад розв'язування прямої та оберненої геодезичних задач на поверхні еліпсоїда на основі чисельного методу (формул Рунге-Кутта) а) алгоритм
- •Пряма геодезична задача
- •Обернена геодезична задача
- •Б) числовий приклад
- •Пряма геодезична задача
- •Обернена геодезична задача
- •3.7.6. Алгоритм та числовий приклад розв'язування прямої та оберненої геодезичних задач в просторі.
- •Обернена геодезична задача
- •Розділ 4 плоскі прямокутні координати гаусса-крюгера
- •4.1. Плоскі координати в геодезії.
- •4.4. Перетворення полярних координат.
- •4.5. Формули проекції Гаусса-Крюгера
- •4.5.2. Формули для обчислення зближення меридіанів
- •4.5.3. Формули для обчислення масштабу проекції
- •Таблиця 4.2
- •Таблиця 4.3
- •Таблиця 4.4
- •Таблиця 4.5
- •Тоді, згідно формули (4.37), для відносного спотворення відстаней, напишемо
- •Таблиця 4.6
- •Таблиця 4.11
- •4.8. Перетворення координат Гаусса-Крюгера із зони в зону.
- •Розділ 5 основи теоретичної геодезії
- •5.1. Сучасні поняття про фігуру Землі та її зовнішнє гравітаційне поле
- •5.2.1. Астрономо-геодезичні відхилення прямовисних ліній
- •5.2.2. Гравіметричні відхилення прямовисних ліній
- •5.2.3. Інтерполювання відхилень прямовисних ліній
- •5.3. Визначення відступів геоїда (квазігеоїда)
- •5.3.1. Астрономічне нівелювання
- •5.3.2. Астрономо-гравіметричне нівелювання
- •5.4. Система висот в геодезії
- •5.4.1. Поняття висоти
- •5.4.1. Ортометричні висоти
- •5.4.3. Нормальні висоти
- •5.4.4. Динамічні висоти
- •5.5.1. Поняття про редукційну задачу
- •5.5.2. Редукування лінійних вимірів
- •5.5.3. Редукування виміряних горизонтальних напрямів
- •5.6.1. Методи виводу розмірів земного еліпсоїда за градусними вимірюваннями
- •5.6.2.Встановлення вихідних геодезичних дат
- •5.6.3. Сучасні підходи до визначення параметрів фігури Землі
5.3.1. Астрономічне нівелювання
Часткові
похідні збурюючого потенціалу
![]() (тут проведена заміна
(тут проведена заміна![]() на
на![]() )
будуть дорівнювати
)
будуть дорівнювати
![]() .
.
Підставимо знайдені значення часткових похідних у формулу (5.14) і отримаємо нові вирази для складових відхилень прямовисних ліній
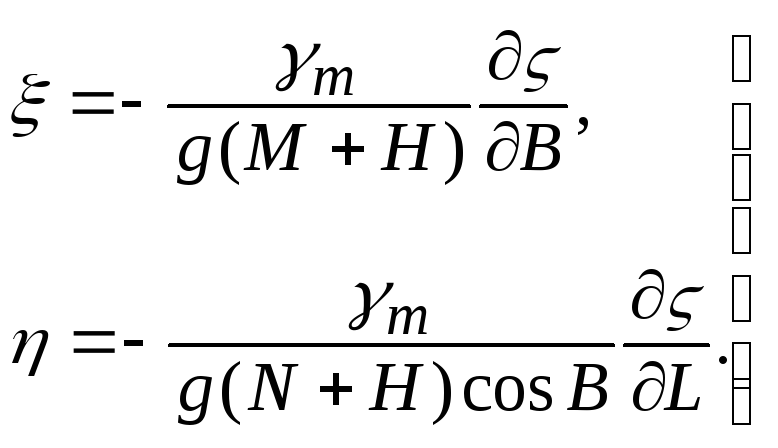 (5.24)
(5.24)
Обчислимо
диференційну зміну відступів геоїда
![]() ,
використовуючи топоцентричну горизонтальну
систему координат
,
використовуючи топоцентричну горизонтальну
систему координат![]() (див. §
1.4).
Якщо висота геоїда є функцією цих
координат, тобто
(див. §
1.4).
Якщо висота геоїда є функцією цих
координат, тобто
![]() ,
то його повний диференціал буде
,
то його повний диференціал буде
![]() .
(5.25)
.
(5.25)
Згідно формули (3.47) має місце ортогональне перетворення координат, тобто відрізки
 (5.26)
(5.26)
складають ортогональну систему координат. З використанням (5.24) та (5.26) для часткових похідних отримаємо
![]() .
.
Зауважимо, що часткова похідна по висоті приведена нами без доведення (детальніше див. [9]). Тепер формулу (5.25) можна записати у такому вигляді
![]() .
.
Поскільки
![]() та
та![]() (див. формулу 3.1), то
(див. формулу 3.1), то
![]() .
.
Проінтегрувавши
останній вираз по ходовій лінії між
точками
![]() та
та![]() на земній поверхні, отримаємо перевищення
геоїда між цими точками
на земній поверхні, отримаємо перевищення
геоїда між цими точками
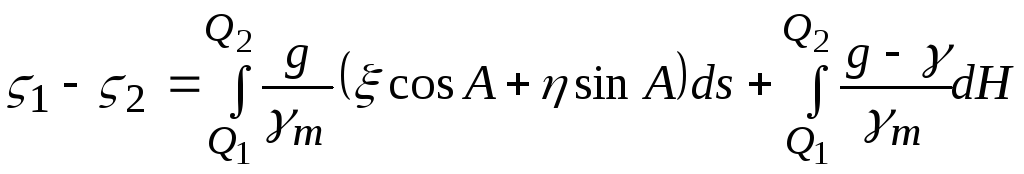 .
(5.27)
.
(5.27)
Формула (5.27) і є формулою астрономічного нівелювання. У цій формулі перший інтеграл є головним, а другий – малою поправкою за відносний надлишок сили ваги.
Отже,
сам процес астрономічного нівелювання
полягає в наступному. Вздовж вибраної
траси повинні бути визначені астрономічні
та геодезичні координати точок, взятих
на відстанях 5-10 км, їх наближені висоти
(будь-яким методом). Необхідно також
провести гравіметричне знімання. Після
отримання всіх необхідних даних
визначають
![]() .
Звісно, в початковій точці астрономічного
нівелювання висота геоїда над земним
еліпсоїдом повинна бути відома. Отримання
різниць
.
Звісно, в початковій точці астрономічного
нівелювання висота геоїда над земним
еліпсоїдом повинна бути відома. Отримання
різниць![]() за формулою (5.27) є досить складною
справою, особливо це стосується обчислення
другого члена. Взагалі ця поправка є
порівняно незначною: в гірських районах
вона може складати до 0.5м, а у рівнинних
– до 0.1м. Зважаючи на величину даної
поправки, а також на той факт, що вона
визначається досить невпевнено, нею
часто нехтують. Тому формулу астрономічного
нівелювання часто записують у спрощеному
варіанті
за формулою (5.27) є досить складною
справою, особливо це стосується обчислення
другого члена. Взагалі ця поправка є
порівняно незначною: в гірських районах
вона може складати до 0.5м, а у рівнинних
– до 0.1м. Зважаючи на величину даної
поправки, а також на той факт, що вона
визначається досить невпевнено, нею
часто нехтують. Тому формулу астрономічного
нівелювання часто записують у спрощеному
варіанті
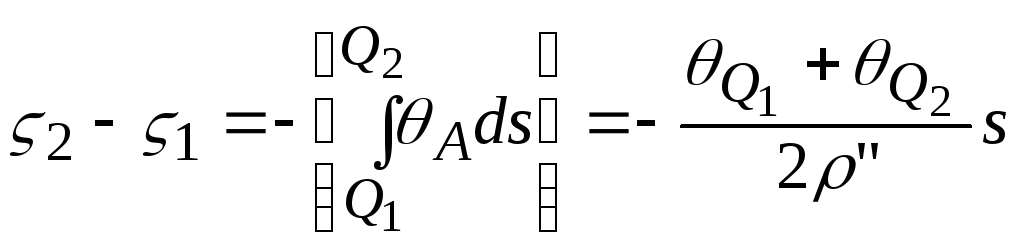 ,
(5.28)
,
(5.28)
де
![]() .
.
Похибка
лінійної інтерполяції астрономо-геодезичних
відхилень прямовисних ліній
![]() визначається
для рівнинних районів виразом (5.21).
Емпірична середня квадратична похибка
астрономічного нівелювання (в м) по
лінії довжиною
визначається
для рівнинних районів виразом (5.21).
Емпірична середня квадратична похибка
астрономічного нівелювання (в м) по
лінії довжиною![]() підраховується за формулою
підраховується за формулою
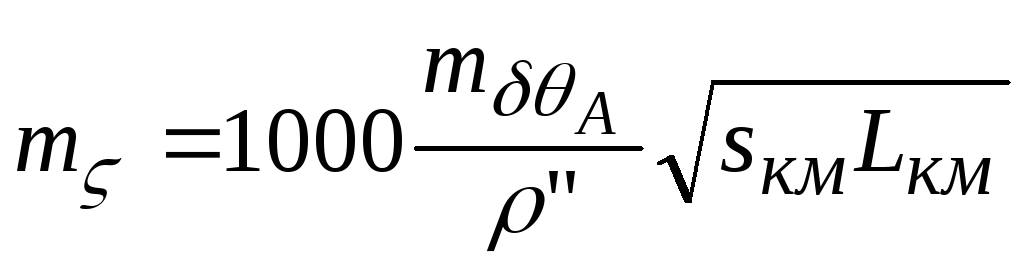 ,
(5.29)
,
(5.29)
де
![]() -відстань
між астропунктами. Для типової в Україні
відстані
-відстань
між астропунктами. Для типової в Україні
відстані![]() маємо
маємо![]() .
Тоді при
.
Тоді при![]()
![]() .
.
Результати астрономічного нівелювання можуть бути суттєво покращені, якщо замість збільшення кількості астропунктів використати інтерпольовані значення астрономо-геодезичних відхилень прямовисних ліній (див. § 5.2.3). Використання інтерпольованих відхилень прямовисних ліній зменшує вплив нелінійності зміни астрономо-геодезичних відхилень прямовисних ліній, але цілком не виключає його.
5.3.2. Астрономо-гравіметричне нівелювання
Астрономічне
нівелювання може бути практично
реалізоване при умові, що в кожній точці
нівелювання відомі астрономо-геодезичні
відхилення прямовисних ліній. Це означає,
що в кожній з цих точок необхідно виконати
астрономічні визначення широти та
довготи, а також передати на на ці точки
геодезичні координати. Для значних
територій це є надзвичайно складна
робота. Відхилення прямовисних ліній
можуть бути отримані чисто гравіметричним
методом з допомогою формул Венінг-Мейнеса
(5.19). В силу вказаних там причин цей метод
теж є малопридатним для даної задачі.
Ще у 1934 р. М. Молоденським був запропонований
спосіб визначення висот геоїда, що
базувався на можливостях астрономо-геодезичного
та гравіметричного методів отримання
відхилень прямовисних ліній. При цьому
він дозволяв обійти труднощі, що
зустрічалися у кожному методі зокрема.
Цей спосіб був названий астрономо-гравіметричним
нівелюванням. Суть цього способу полягає
у тому, що відхилення прямовисної лінії
![]() між віддаленими пунктами
між віддаленими пунктами![]() і
і![]() можуть бути інтерпольовані за матеріалами
гравіметричного знімання та
астрономо-геодезичними даними.
Інтерполювання проводиться згідно
методики, що описана у § 5.2.3. Це дає змогу
врахувати нелінійність зміни
астрономо-геодезичних відхилень
прямовисних ліній між суміжними
астрономічними пунктами.
можуть бути інтерпольовані за матеріалами
гравіметричного знімання та
астрономо-геодезичними даними.
Інтерполювання проводиться згідно
методики, що описана у § 5.2.3. Це дає змогу
врахувати нелінійність зміни
астрономо-геодезичних відхилень
прямовисних ліній між суміжними
астрономічними пунктами.
Якщо
витримані умови астрономо-гравіметричного
методу, то середня квадратична похибка
астрономо-гравіметричного нівелювання
підраховується за формулою (5.29).
Враховуючи, що точність
![]() ,
середня відстань між суміжними
астропунктами складає
,
середня відстань між суміжними
астропунктами складає![]() ,
то при
,
то при![]()
![]() .
.
