8. Перестановки з повтореннями

Формулу для кількості перестановок Р_п одержують із формули для кількості розміщень без повторень:

Приклад 8.1. Знайдемо кількість рядків, які можна утворити, переставляючи букви слова SOFTWARE. Оскільки жодна буква тут не повторюється, то можна утворити Р₈ =8!=40320 рядків. ▲

Розглянемо складніший вид перестановок.

Означення 8.1. Нехай є n елементів k різних типів, а число n_j (j=1,…,k) — кількість елементів j-гo типу. Очевидно, що n₁+п₂+...+n_k=п. Перестановки з n елементів за такої умови називають перестановками з повтореннями. Кількість таких перестановок позначають як .

ТЕОРЕМА 8.1. Кількість різних перестановок з повтореннями рівна:

.

Доведення. Щоб знайти явний вираз для ,візьмемо окрему перестановку та замінимо в ній усі однакові елементи різними. Тоді кількість різних перестановок, котрі можна отримати з узятої однієї перестановки, дорівнює . Якщо зробити це для кожної перестановки, то одержимоn! перестановок. Отже, , звідки

.▲

Приклад 8.2. Знайдемо, скільки рядків можна утворити, переставляючи букви слова POSSESSIONLESSNESSES. У цьому слові є повторні входження букв, тому скористаємося формулою для перестановок із повтореннями:

69837768000 слів. ▲

Задача розкладання в ящики. Дано n різних предметів і k ящиків. Потрібно покласти в перший ящик n₁ предметів, у другий — n₂ предметів,…, k-й — n_k предметів, де . Тут— фіксовані числа. Скількома способами можна це зробити?

Розв’язання.

1-й спосіб. Занумеруємо всі n предметів. Кожен предмет попадає у свій ящик:

1-й предмет	2-й предмет	…	…	n-й предмет
a1 ящик	a2 ящик	…	…	an ящик

Як бачимо, кожному розподілу предметів по ящиках відповідає певна послідовність a₁a₂…a_n. Кількість всіх послідовностей відповідає кількості способів розподілу предметів.

Послідовність a₁a₂…a_n є перестановкою з повтореннями чисел {1, 2,  …, k}, бо перестановкою її елементів ми отримаємо інакший розподіл, а її елементи повторюються. Очевидно, що “1” повторюватиметься n₁ разів, “2” повторюватиметься n₂ разів, і т.д. Отже, кількість розкладань:

.

2-й спосіб.

Серед п предметів візьмемо довільну n₁ підмножину й покладемо її в перший ящик (це можна зробитиспособами). Середп-п₁ предметів, що залишились, візьмемо n₂ підмножину, покладемо її в другий ящик (це можна зробити способами) і продовжимо цей процес. За правилом добутку загальна кількість розкладань дорівнює:

▲

9. Генерування розбиття множини

Нагадаємо, що розбиттям множини називають сукупність непорожніх множин, які не перетинаються між собою, а їх об’єднання дає вхідну множину A.

Приклад 9.1. Задано множину A = {1, 2, 3}. Знайдемо усі її розбиття: {{1, 2, 3}}, {{1,2}, {3}}, {{2,3}, {1}}, {{1,3}, {2}}, {{1}, {2}, {3}}. ▲

Отримати розбиття множини прямим методом доволі складно. Алгоритм запропонований нижче полягає у тому, що кожне розбиття множини {1, 2, …, п-1,  п} можна отримати із розбиття {1, 2, …, п-1}, додавши елемент {п}. Алгоритм має недолік: він вимагає попереднього обчислення всіх розбиттів множин із кількістю елементів 1, 2, 3, 4, …n-1. Існують алгоритми, які можуть робити прямий перебір без додаткових обчислень, але вони суттєво складніші.

Алгоритм перебору всіх розбиттів множини.

Крок 1. Нехай n = 1. Розбиття множини A = {1} є єдине M₁= {{1}}. Збільшуємо n на одиницю.

Крок 2. Робимо присвоєння n=n+1. На попередньому кроці ми обчислили усі розбиття M_n-1 множини {1, 2, …, п-1}. Ініціалізуємо розбиття M_n порожньою множиною.

Крок 3. Для кожного з розбиттів множини {1, 2, …, п-1,  п} елемент {п} почергово додаємо до кожної з множин розбиття. Отримане розбиття додаємо до M_n. Зауваження: для цього треба організувати подвійний цикл.

Крок 4. Утворюємо розбиття множини {1, 2, …, п-1,  п}, додаючи елемент {п} як окрему множину до кожного з розбиттів елементу A та додаємо до M_n.

Крок 5. Переходимо до кроку 2, якщо n не досягло кінцевого значення. ▲

Розглянемо детальніше рекурсивну роботу алгоритму.

Приклад 9.2. Знайдемо розбиття множини M₃.

Крок 1. Нехай n = 1. Розбиття множини A = {1} є єдине – M₁= {{1}}.

Крок 2. n = 2. Ініціалізуємо M₂= {}.

Крок 3. Додаємо до M₂ розбиття {{1,2}}.

Крок 4. Додаємо до M₂ розбиття {{1},{2}}.

Крок 5. Ми отримали розбиття M₂ =[{{1,2}};{{1},{2}}] і переходимо до кроку 2.

Крок 6. Ініціалізуємо M₃= {}. Збільшуємо n на одиницю, n=3.

Крок 7. Додаємо до M₃ розбиття елемент {3}, до кожної з множин розбиттів {{1,2}} та {{1},{2}}.

Отримуємо: M₃ =

Як бачимо із розбиття {{1},{2}}, ми отримали 2 нових розбиття, а з {{1,2}} – лише одне.

Крок 8. Додаємо до M₃ розбиття, які отримуються від додавання елементу {3}, до кожної з множин розбиття {{1,2}} та {{1},{2}} як окремої множини.

Отримуємо: M₃ =

Крок 9. Оскільки n=3, то алгоритм завершено. ▲

Означення 9.1. Кількість усіх розбиттів n-елементної множини на непорожні частини називають числами Белла і позначають S(п).

Означення 9.2. Кількість розбиттів n-елементної множини на k непорожніх частин називають числами Стірлінга другого роду і позначають S (п, k).

З розглянутого прикладу 9.2:

S(3, 1) = 1; S(3, 2) = 3; S(3, 3) = 1; S(3) = 1 + 3 +1 = 5.

Зв’язок між числами Белла та числами Стірлінга очевидний:

Але для них також виконуються рівності:

;

;

.

Останню рівність легко вивести з алгоритму для генерування множин. Також за її допомогою легко виводити значення чисел Белла та Стірлінга 2-го роду (табл. 9.1).

Таблиця 9.1

n\k	1	2	3	4	5	6	…
1	1						…	1
2	1	1					…	2
3	1	3	1				…	5
4	1	7	6	1			…	15
5	1	15	25	10	1		…	52
6	1	31	91	65	15	1	…	203
…	…	…	…	…	…	…	…	…

Означення 9.3. Послідовність дійсних чисел називаютьунімодальною, якщо існує такий натуральний номер m, що , тобто:

• послідовність строго зростає на відрізку

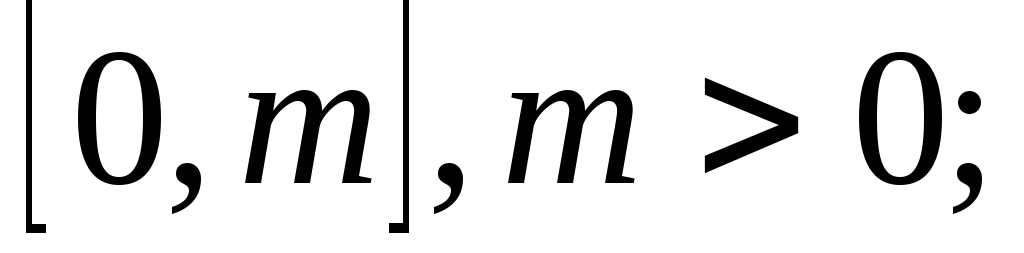
• послідовність строго спадає на відрізку

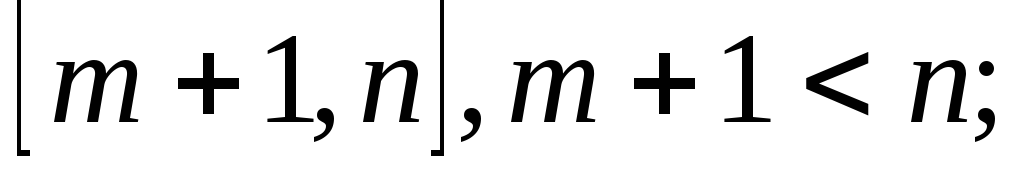
• максимальне значення досягається не більш ніж у двох точках: m і можливо, m+1.

ТЕОРЕМА 9.1. За фіксованого п послідовність k = 1, 2, ..., n унімодальна.