5. Відношення еквівалентності

Означення 5.1. Відношення на множині А називають відношенням еквівалентності, якщо воно рефлексивне, симетричне й транзитивне. Два елементи множини А, які зв'язані відношенням еквівалентності, називають еквівалентними.

Приклад 5.1. Нехай – відношення на множині цілих чисел, так що аb тоді й тільки тоді, коли вони рівні за модулем . Це відношення має властивості:

• рефлективності: ;

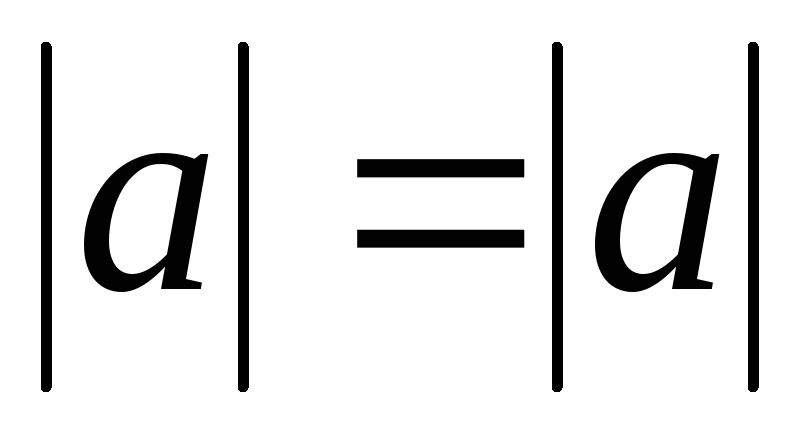• симетричності: якщо , то;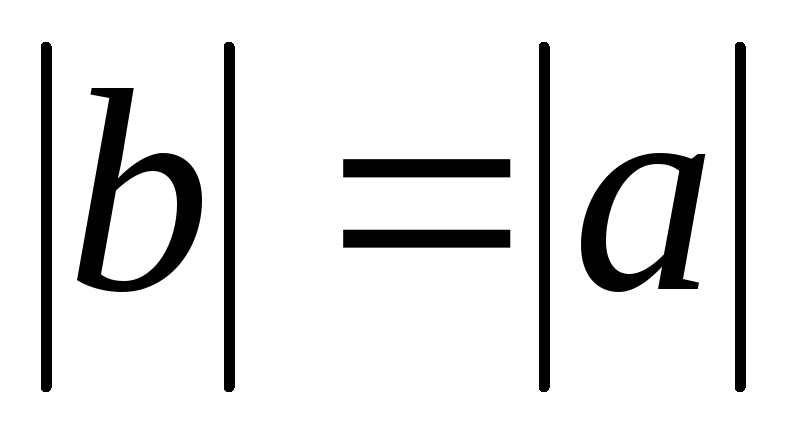

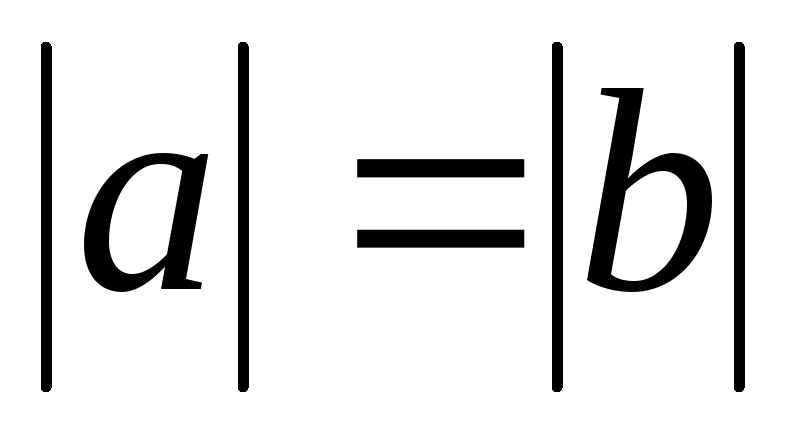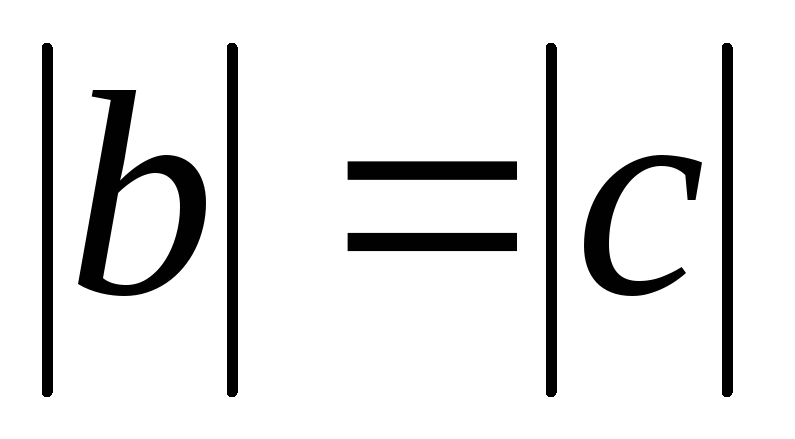• транзитивності. якщо і, то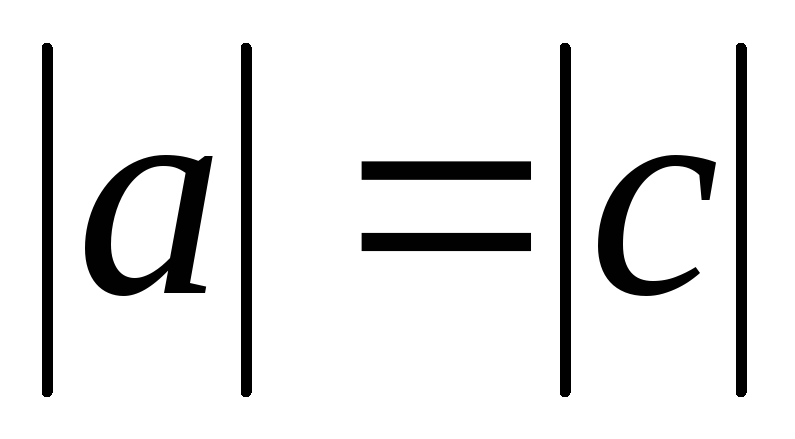: отже, це відношення еквівалентності. ▲

Приклад 5.2 (конгруентність за модулем т). Покажемо, що відношення ={(a, b)| аb(mоd т) } є відношенням еквівалентності на множині цілих чисел, де т – натуральне число і т > 1. є. За означенням аb(mоd т) означає, що т націло ділить (а-b).

Розглянемо рефлективність: аа(mоd т), бо а-а=0, а 0 націло ділиться на m. Отже, відношення рефлексивне.

Далі, аb(mоd т), якщо а-b=kт, де k – ціле. Отже, b-а=(-k)т, тобто bа(mоd т), відношення симетричне.

Нарешті, нехай аb(mоd т), bс(mоd т). Це означає, що а-b=kт, b-с=lт, де k,l – цілі. Додамо останні дві рівності: а-b+b-с = (k+l)т, тобто а-с= (k+l)т. Отже, ас(mоd т), відношення транзитивне.

Таким чином, конгруентність за модулем т є відношенням еквівалентності на множині цілих чисел. ▲

З відношенням еквівалентності тісно пов’язане поняття класу еквівалентності й розбиття множини на класи.

Оскільки відношення еквівалентності за означенням рефлексивне, то в будь-якому відношенні еквівалентності кожний елемент є еквівалентним до самого себе. Більше того, оскільки відношення еквівалентності за означенням транзитивне, то з того, що а та b еквівалентні, b та с еквівалентні, випливає, що а та с еквівалентні.

Означення 5.2. Нехай є відношенням еквівалентності на множині А. Множину всіх елементів, які еквівалентні до елемента аА, називають класом еквівалентності (елемента а). Клас еквівалентності, який породжений елементом а за відношенням , позначають [а]_R. Якщо мають на увазі певне відношення еквівалентності, то використовують позначення [а]. Отже: [а]_R={s| (а, sR}. Якщо b[а]_R, то b називають представником цього класу еквівалентності.

Приклад 5.3. Знайдемо класи еквівалентності відношення із прикладу 5.1. Оскільки ціле еквівалентне само собі та протилежному числу, то класи еквівалентності за цим відношенням такі: [а]={-а, а}, а0 та [0]={0}.▲

Приклад 5.4. Знайдемо класи еквівалентності елементів 0 та 1 для відношення конгруентності за mod 4 (див. приклад 5.2). Клас еквівалентності елемента 0 містить усі цілі b такі, що 0b(mod 4). Цілі в цьому класі, очевидно, такі, що діляться на 4. Отже, [0]={..., -8, -4, 0, 4, 8, ...}. Клас еквівалентності елемента 1 містить усі цілі b такі, що 1(mod 4). Таким чином, [1]={..., -7, -3, 1, 5, 9, ...}. Класи еквівалентності типу розглянутих у цьому прикладі називають класами конгруентності за модулем т. Клас конгруентності за модулем т позначають [а]_т. Отже, [0]₄={..., -8, -4, 0, 4, 8, ...}, [1]₄={...,-7, -3, 1, 5, 9, ...}.▲

Нехай R – відношення еквівалентності на множині А. Важливо зазначити, що класи еквівалентності, породжені двома елементами множини А, або збігаються, або не перетинаються. Наступна теорема стверджує цей факт.

Теорема 5.1. Нехай – відношення еквівалентності на множині А. Тоді такі твердження рівносильні:

(І) аRb; (II) [а]=[b]; (III) [а][b].

Доведення. Спочатку доведемо, що з (І) випливає (II). Припустимо, що аRb. Для того, щоб довести рівність [а]=[b], покажемо, що [a][b] та [b][а]. Нехай с[a], тоді ас. Оскільки аb та симетричне відношення, то bRа. Більше того, оскільки відношення R транзитивне, то з bа та ас випливає bс. Отже, [а][b]. Аналогічно доводиться, що [b][а].

Доведемо тепер, що з (II) випливає (III). Дійсно [а], оскільки а[а] через рефлексивність. Отже, з [а]=[b] випливає [а][b].

Нарешті, доведемо, що з (III) випливає (І). Припустимо, що c[а] та c[b]. Тоді існує елемент с такий, що с[а] та c[b], тобто ас та bс. Із симетричності відношення й випливає сb. Оскільки відношення R транзитивне, то з ас та сb випливає аb.

Оскільки з (І) випливає (II), з (II) випливає (III) та з (III) випливає (І), то три твердження (І), (II) та (III) рівносильні. ▲

Кожне відношення еквівалентності породжує розбиття множини А (на класи еквівалентності). Справді, з теореми 2.1 випливає, що і, якщо, то .Нагадаємо, що розбиттям множини А називають таку систему множин , iI (I – множина індексів), що: для всіхiI, дляijта .

Приклад 5.5. Відношення конгруентності за mod 4 (див. приклад 5.4) породжує розбиття множини Z цілих чисел на 4 класи: [0]₄, [1]₄, [2]₄ та [3]₄. Ці класи попарно не перетинаються, а їхнє об'єднання дорівнює множині Z. ▲

Матриця відношення еквівалентності. Нехай відношення еквівалентності задано в множині A.

Елементи, що належать одному класу еквівалентності, попарно еквівалентні між собою. Отже, стовпці матриці відношення еквівалентності для елементів одного класу еквівалентності однакові та містять одиниці у всіх рядках, які відповідають цим елементам. Оскільки класи еквівалентності не перетинаються, у стовпцях, які відповідають елементам різних класів, не буде одиниць в одних і тих самих рядках.

Приклад 5.6. Для відношення еквівалентності, заданого класами еквівалентності . При побудові матриці відношення розташуємо елементи множини так, щоб ті елементи, які належать одному класу еквівалентності, були поруч. Тоді одиничні елементи матриці відношення еквівалентності утворять непересічні квадрати, діагоналі яких розташовуються на головній діагоналі матриці:

	1	1	1	0	0	0	0	0	0
	1	1	1	0	0	0	0	0	0
	1	1	1	0	0	0	0	0	0
	0	0	0	1	1	0	0	0	0
	0	0	0	1	1	0	0	0	0
	0	0	0	0	0	1	1	1	1
	0	0	0	0	0	1	1	1	1
	0	0	0	0	0	1	1	1	1
	0	0	0	0	0	1	1	1	1