16.3. Координати вектора

Якщо на площині задано два взаємно перпендикулярні (базис­ні) вектори і, такі щото будь-який векторплощини можна в єдиний спосіб подати у вигляді:

.

Величини х_а і у_а називаються координатами вектора . Позначають:.

Аналогічно, якщо у просторі задано три взаємно перпендикулярні вектори ,і, то будь-який векторпростору можна в єдиний спосіб подати у вигляді

де x_a, y_a, z_a — координати вектора . Позначення:.

Властивості координат вектора

1. Рівні вектори мають рівні координати, тобто якщо , тоx_a = x_b, y_a = y_b, z_a = z_b.

2. При множенні вектора на число його координати множать на те саме число, тобто якщо тоx_a = λx_b, y_a = λy_b, z_a = λz_b.

3. При додаванні векторів їхні координати додають, тобто якщо тоx_c = x_a + x_b, y_c = y_a + y_b, z_c = z_a + z_b.

4. Скалярний добуток двох векторів дорівнює сумі добутків відповідних координат цих векторів:

. (1)

5. Модуль вектора дорівнює кореню квадратному із суми квад­ратів його координат:

(2)

Якщо у просторі дві точки А(х₀, y₀, z₀) задано їхніми координатами і В(х₁, y₁, z₁), то вектор має координати, що дорівнюють різниці відповідних координат початку і кінця вектора, тобто

Задача. Знайти координати точки D і кут між діагоналями паралелограма ABCD, якщо А(0, 1, – 2), В(– 1, 0, 3), С(2, 3, – 1).

• Нехай точка D має координати (х, у, z). Знайдемо координати векторів і:

Оскільки ABCD — паралелограм, то Звідси випливає, щох = 3, у – 1 = 3, z + 2 = – 4, тобто х = 3, у = 4, z = – 6. Знайдемо тепер координати діагоналей:

Використовуючи формулу (2) для довжини вектора і формулу (1) для скалярного добутку векторів через його координати, ді- стаємо:

16.4. Векторний добуток

Векторним добутком двох векторів іназивається векторщо задовольняє такі умови:

1)

2) , α — кут міжі;

3) трійка ,імає праву орієнтацію, тобто з кінця вектораповорот від векторадо векторана найменший кут бачимо проти годинникової стрілки (рис. 1).

Рис. 1

Властивості векторного добутку

1. Антикомінативність:

2. Дистрибутивність:

3. Асоціативність множення на скаляр:

4. Умова колінеарності двох векторів:

Геометричний зміст векторного добутку

Площа паралелограма, побудованого на векторах і, дорів­нює модулю їхнього векторного добутку (рис. 2):

Рис. 2

Площа трикутника, побудованого на векторах і, дорівнює половині модуля їхнього векторного добутку (рис. 3):

Рис. 3

Векторний добуток у координатах

Якщо вектори ізадано їхніми координатамиі, то векторний добуток цих векторів має коорди- нати:

Замість наведеної громіздкої формули зручніше використовувати запис векторного добутку через визначник:

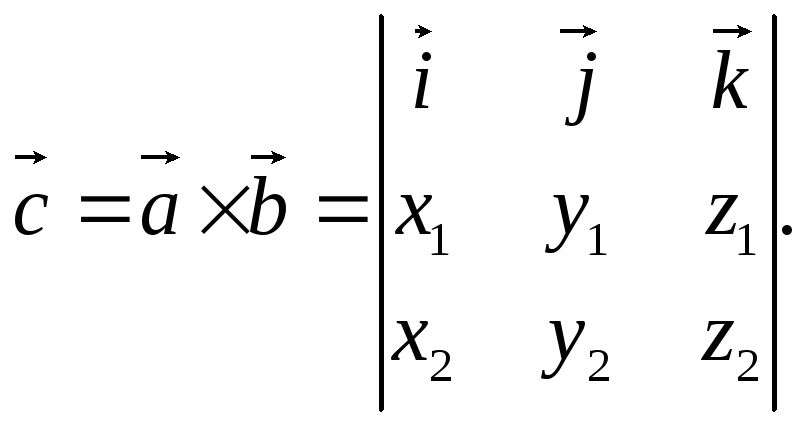
Тут — одиничні вектори прямокутної системи координат. Якщо розкрити визначник за першим рядком, то коефіцієнти при векторахдадуть відповідні координати вектора

Задача. Знайти площу трикутника з вершинами в точках А(2, –4, 1), В(–2, 1, 3), C(l, –1, 2).

• Насамперед введемо вектори, що збігаються з двома сторонами трикутника АВС:

,

або

208

Елементарна математика