
- •15.1. Основні поняття планіметрії. Трикутники та їхні властивості
- •Основні ознаки рівності довільних трикутників
- •15.2. Паралельність. Паралелограм і трапеція. Подібність трикутників
- •Ознаки паралельності
- •Ознаки подібності трикутників
- •15.3. Чотирикутники
- •15.4. Коло і круг. Число π
- •15.5. Визначні точки в трикутнику
- •15.6. Метричні теореми планіметрії. Формули площі трикутника
- •1. У рівнобедреному прямокутному трикутнику гострі кути дорівнюють по 45°, а відношення гіпотенузи до катета дорівнює
- •2. Катет прямокутного трикутника, що лежить проти кута 30°, дорівнює половині гіпотенузи.
- •15.7. Основні аксіоми та найпростіші теореми стереометрії
- •1. Через три точки, що не лежать на одній прямій, можна провести єдину площину (аксіома площини).
- •2. Якщо дві точки належать одній площині, то й пряма, що їх сполучає, належить цій площині.
- •3. Якщо дві різні площини мають спільну точку, то вони мають спільну пряму — лінію перетину цих площин.
- •15.8. Перпендикулярність у просторі. Проекція прямої. Двогранний кут
- •Властивості, проектування
- •15.9. Многогранники. Площі поверхонь. Об’єм многогранників
- •15.10 Циліндр. Конус. Сфера, куля та її частини
- •16.1. Означення та основні властивості векторів
- •16.2. Скалярний добуток векторів, його властивості
- •16.3. Координати вектора
- •16.4. Векторний добуток
Ознаки паралельності
1. Якщо при перетині двох прямих третьою внутрішні (зовнішні) різносторонні кути рівні, то прямі паралельні.
2. Якщо при перетині двох прямих третьою відповідні кути рівні, то прямі паралельні.
3. Якщо при перетині двох прямих третьою сума внутрішніх (зовнішніх) односторонніх кутів дорівнює 180°, то прямі паралельні.
Властивості паралельних прямих формулюються як твердження, обернені до ознак. Наприклад: Якщо дві паралельні прямі перетинаються третьою, то внутрішні (зовнішні) різносторонні кути рівні.
Наведемо теореми і означення, пов’язані з паралельністю прямих.
Теорема 1. Сума внутрішніх кутів трикутника дорівнює 180°.
Паралелограмом називається чотирикутник, протилежні сторони якого попарно паралельні.
Ознаки паралелограма
1. Якщо дві протилежні сторони чотирикутника рівні і паралельні, то цей чотирикутник — паралелограм.
2. Якщо діагоналі чотирикутника в точці перетину поділяються навпіл, то цей чотирикутник — паралелограм.
3. Якщо протилежні кути чотирикутника попарно рівні, то цей чотирикутник — паралелограм.
Властивості паралелограма формулюються як твердження, обернені до ознак паралелограма. Наприклад: У паралелограмі діагоналі точкою перетину поділяються навпіл.
Трапецією називається чотирикутник, дві протилежні сторони якого паралельні. Ці сторони називають основами трапеції. Дві інші непаралельні сторони трапеції називають бічними. Трапеція називається рівнобедреною, якщо її бічні сторони рівні. Трапеція називається прямокутною, якщо одна з її бічних сторін перпендикулярна до основ.
Теорема 2 (теорема Фалеса). Якщо на прямій а відкласти кілька рівних відрізків і через їхні кінці провести паралельні прямі, то ці прямі відітнуть на будь-якій іншій прямій b рівні між собою відрізки (рис. 2), тобто якщо АВ = ВР = CD, то A1B1 = B1C1 = C1D1.
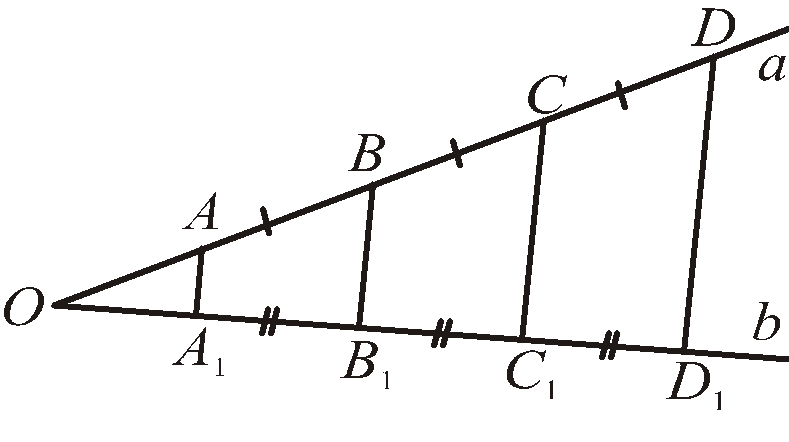
Рис. 2
Наслідок.
Паралельні
прямі відтинають на сторонах кута
відповідно пропорційні відрізки, тобто
справджується співвідношення:
![]() (рис. 2).
(рис. 2).
На підставі теореми Фалеса доводять три важливі для розв’язування задач теореми.
Теорема 3 (про середню лінію). Середня лінія трикутника (лінія, що сполучає середини двох його сторін) паралельна третій його стороні і дорівнює її половині.
Теорема 4. Середня лінія трапеції (лінія, що сполучає середини бічних її сторін) паралельна основам і дорівнює їхній півсумі (рис. 3).
![]()
Рис. 3
Задача. У трапеції ABCD паралельні сторони мають відповідно довжини ВС = 12, AD =20. Знайти довжини трьох відрізків, на які діагоналі АС і BD поділяють середню лінію трапеції (рис. 4).
МР — середня лінія Δ АВС. Тому за теоремою 2 маємо:

2.
QN
—
середня лінія Δ ВDC;
відповідно
![]()
3.
MN
— середня лінія трапеції ABCD,
тому за теоремою 3 маємо:
![]()
4. PQ = MN – MP – NQ = 16 – 6 – 6 = 4. Дістаємо: МР = NQ = = 6, PQ = 4.

Рис. 4
Теорема
5
(про бісектрису внутрішнього кута
трикутника).
Бісектриса
внутрішнього кута довільного трикутника
поділяє протилежну сторону на відрізки,
пропорційні до прилеглих сторін:
![]() (рис. 5, а).
(рис. 5, а).
Задача. У прямокутному трикутнику АВС (рис. 5, б) АС = 3, ВР = 4. Знайти довжини відрізків, на які бісектриса AD поділяє сторону ВС, а також довжину бісектриси AD.
За теоремою Піфагора знаходимо

2.
Нехай AD
— бісектриса
![]() CAB.
Позначимо CD
= x,
тоді
BD
=
4 – x.
CAB.
Позначимо CD
= x,
тоді
BD
=
4 – x.
3.
За теоремою 5 маємо
![]() Звідси
Звідси![]()
4.
За теоремою Піфагора для
![]() CAB
дістанемо AD2
= АС2
+ + CD2.
Тому
CAB
дістанемо AD2
= АС2
+ + CD2.
Тому
![]() Остаточно маємо:
Остаточно маємо:![]()
![]()
![]()
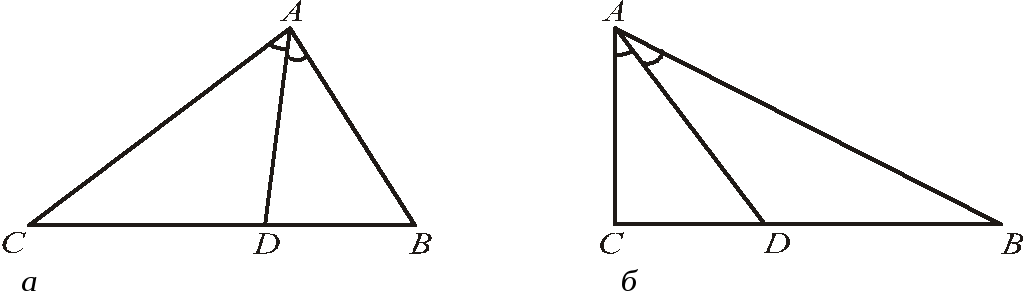
Рис. 5
Два трикутники називаються подібними, якщо їхні відповідні кути рівні, а відповідні сторони пропорційні.
