5.9. Заміна радикалів новими невідомими

Основним способом рішення складних ірраціональних рівнянь є заміна кожного радикала новим невідомої. Це дозволяє звести ірраціональне рівняння до системи алгебраїчних рівнянь.

Приклад. Розв’яжемо рівняння

.

Уведемо позначення

,

і при цьому приходимо до системи алгебраїчних рівнянь

.

У першу чергу виключаємо невідоме .

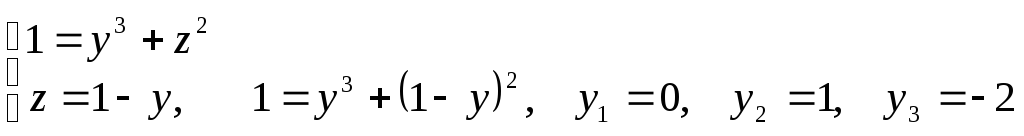
Звідси знаходимо рішення ,,.

Приклад. Розв’яжемо рівняння

.

Позначимо радикали

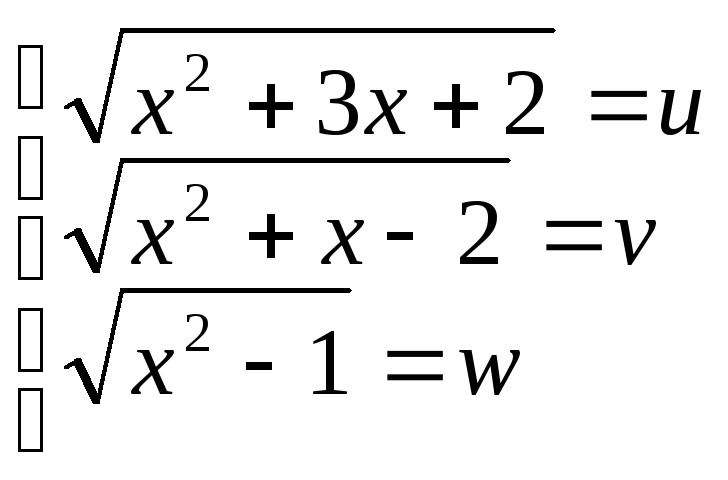
Рівняння зводиться і системі рівнянь

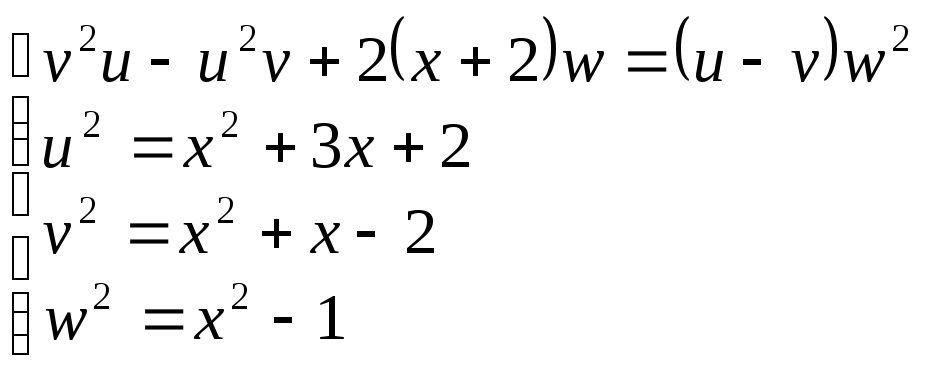
У першу чергу виключаємо невідоме

.

Одержимо рівняння

.

Яке розкладається на множники

.

Вирішуємо рівняння

Корень не задовольняє рівнянню.

Приклад. Розв’яжемо рівняння

.

Уводимо позначення

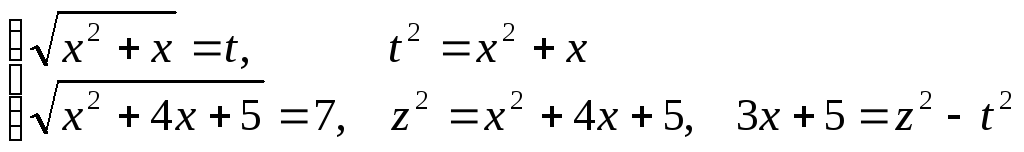
Рівняння зводиться до системи рівнянь

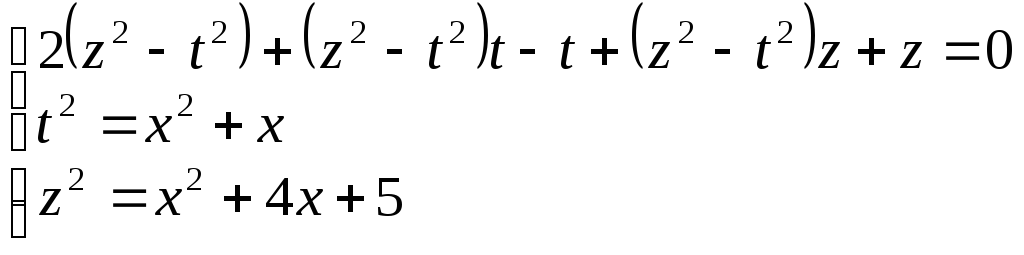
Розкладемо перше рівняння на множники

.

Вирішуємо рівняння

1)

2) ,.

5.10. Уведення параметра (представив Саушкин о. Ф.)

Також як і в алгебраїчні рівняння можна вводити допоміжний параметр, що спрощує рішення рівнянь.

Приклад. Розв’язати рівняння

.

Запишемо рівняння у виді

.

Заміна приводить рівняння до виду

.

Уводимо параметр , думаючи.

Одержимо ірраціональне рівняння з параметром

, .

Одержимо квадратне рівняння відносно

.

Знаходимо рішення

, .

Для відшукання одержимо рівняння

, ,

, ,.

Звідси знаходимо значення

, ,,.

Корені ,— сторонні.

Приклад. Розв’язати рівняння

.

Уводимо параметр . Одержимо рівняння

, .

Звільняючись від ірраціональності, одержимо рівняння

, .

Підставляючи значення , одержимо рішення

, ,

, ,.

Рівняння задовольняє лише корінь .

Приклад. Розв’язати рівняння

.

Знаходимо ОДЗ

.

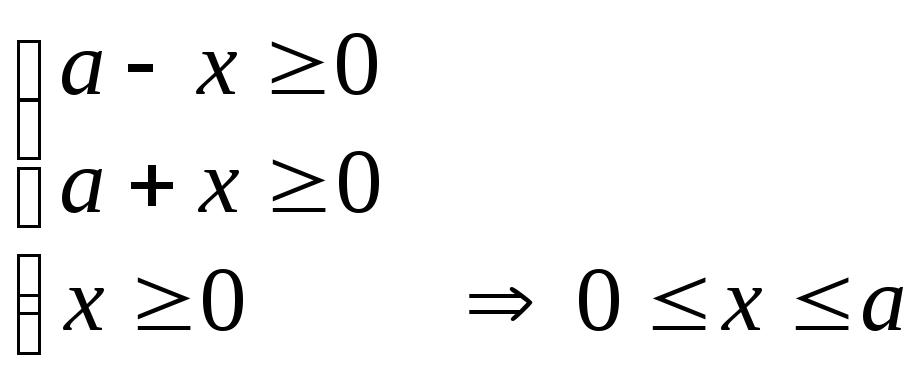Зводимо обох частин рівняння в квадрат

;

, ,,.

Корінь не входить в ОДЗ. Якщо, то. Знайдемо значення, при яких маємо корінь. Підставимоу вихідне рівняння

;

, ;.

Відповідь: при;при.

5.11. Рівняння з модулями

Рівняння з модулями примикають до ірраціональних рівнянь, тому що

. (6)

Звичайно використовують визначення по формулі.

.

Приклад. Вирішити рівняння

.

Припустимо, що й одержимо рівняння. Якщо, то,.

Приклад. Вирішити рівняння

.

Знайдемо крапки, у яких модулі звертаються в нуль

, ;,.

Ці крапки розбивають числову вісь на частині, у кожній з який вираження під знаком модуля не змінюють знак.

1) ;,;

2) ;,маємо тотожності;

3) ;,. Відповідь.

Приклад. Вирішити рівняння

.

Знайдемо крапки, де ,,. Розглядаємо всілякі окремі випадки.

1) ,,;

2) ;,;

3) ;,.

Приклад. Розв’язати систему рівнянь

Розглянемо усілякі випадки

1) ,

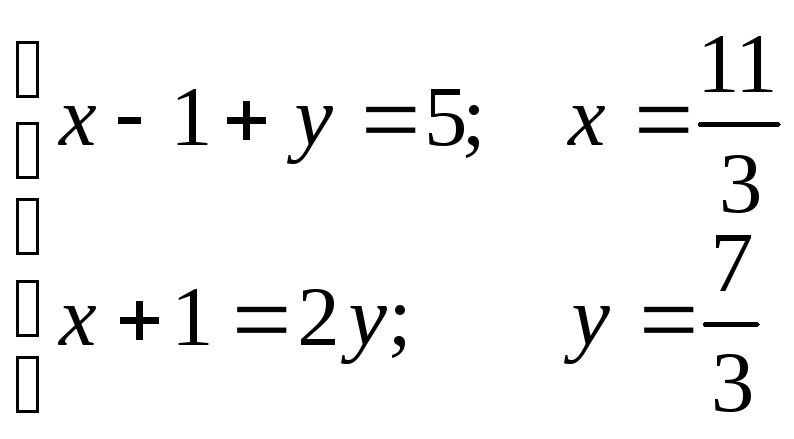. Знайшли рішення системи.

2) ,

. Рішення не задовольняє умові.

3) ,

. Рішення не задовольняє умові.

4) ,

. Знайшли рішення системи.

З формули (6) випливають правила внесення і винесення множників під радикал

. (7)

Якщо множник вноситься під радикал, то поза радикалом залишається знак множника.

Приклад. Розв’язати рівняння

.

Помножимо рівняння на ,.

.

Розглянемо можливі випадки.

1) . Вносимо позитивний множник під знак радикала

, ,

, .;,.

Корінь не задовольняє умові. Відповідь.

2) . Вносимо негативний множник під знак радикала по формулі (7)

, ,,,.

, ,. Коріньне задовольняє умові. Відповідь.