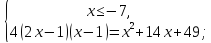2. Ірраціональні рівняння і нерівності

Рівняння, у яких змінна міститься під знаком кореня, називають ірраціональними.

Найчастіше розв’язування ірраціональних рівнянь ґрунтується на зведені заданого рівняння за допомогою деяких перетворень до раціонального рівняння. Як правило , цього досягають піднесенням обох частин ірраціонального рівняння до одного й того самого степеня, за потреби кілька разів.

Приклад 1. Розглянемо рівняння

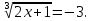
Розв’язання. Підносячи обидві частини рівняння отримаємо рівняння, рівносильне даному. Маємо:

Відповідь: -14

Функція  оборотна, то міркування використані при розв’язування рівняння узагальнимо у теоремі.

Теорема 1. Якщо обидві частини ірраціонального рівняння піднести до непарного степеня, то отримаємо рівняння рівносильне даному (на його ОДЗ).

Доведення. Покажемо, що рівняння

(1)

і

(2)

є рівносильними. Нехай число α – корінь рівняння (1). Тоді маємо правильну числову рівність . Звідси можна записати:

Отже, число α є коренем рівняння (2)

Нехай число β – корінь рівняння (2). Тоді отримаємо, що

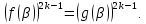
Оскільки функція , є оборотною, то . Отже, β корінь рівняння (1).

Ми показали, що кожний корінь рівняння (1) е коренем рівнин (2) і навпаки. Це означає, що рівняння (1) і (2) рівносильні.

Приклад 2. Розгляжемо рівняння

Розв’язання. Піднесемо обидві частини рівняння до сьомого степеня. Отримаємо рівносильне рівняння:

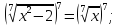
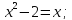
Відповідь: -1;2.

Приклад 3. Розглянемо рівняння (3)

Розв’язання. Природно замінити це рівняння на таке:

(4)

Звідси .

Але перевіривши бачимо, що число не є коренем початкового рівняння. Отже, рівняння (3) не має коренів. Причина появи стороннього кореня полягає в тому, що застосування формули призводить до розширення області визначення рівняння. Тому рівняння (4) є наслідком рівняння (3).

Ще однією причиною появи сторонніх коренів при розв’язуванні ірраціональних рівнянь є необоротність функції Це означає, що з рівності 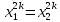не обов’язково випливає, що . Наприклад, , але Водночас із рівності 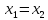випливає рівність .

Наведені міркування сформулюємо теоремою.

Теорема 2. При піднесенні обох частин рівняння до парного степеня отримане рівняння є наслідком даного. В якому можуть виникати сторонні корені, які відсіюються перевіркою.

Доведення. Покажемо, що рівняння

(5)

є наслідком рівняння

(6)

Нехай числа α  корінь рівняння (6), тобто . Тоді

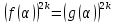. Отже, число α є коренем рівняння (5).

Ми показали, що кожен корінь рівняння (6) є коренем рівняння (5). Це означає, що рівняння (5) є наслідком рівняння (6).

Зауважимо, що коли число β  корінь рівняння (5), то з рівності не обов’язково випливає, що 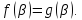Тому в результаті переходу від рівняння 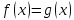до наслідку можуть з’явитися сторонні корені, які можна виявити за допомогою перевірки.

Приклад 4. Розглянемо рівняння

Розв’язання. Піднесемо обидві частини рівняння до квадрата, отримаємо рівняння, яке є наслідком даного:

Перевірка показує, що число 1 є стороннім коренем, а число 4 задовольняє дане рівняння.

Відповідь: 4.

Приклад 5. Розглянемо рівняння

Розв’язання. Піднесемо обидві частини даного рівняння до квадрата:

Звідси .

Переходячи до рівняння-наслідку, отримуємо:

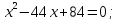
Перевіривши бачимо, що число 42 є стороннім коренем, а число 2 задовольняє дане рівняння.

Відповідь: 2

Розглянемо розв’язування ірраціональних рівнянь за допомогою заміни змінних.

Якщо до рівняння змінна входить в одному і тому самому вигляді, то зручно відповідний вираз із змінною позначити однією буквою (новою змінною)

Приклад 6. Розв’яжіть рівняння .

Позначимо . Тоді . Одержуємо рівняння:

Виконуємо обернену заміну: , тоді або −, звідси х = –8.

Відповідь: 1; –8.

Приклад 7. Розв’яжіть рівняння

Розв’язання. Нехай Одержуємо

Тоді

Звідси

— задовольняє умові ;

— не задовольняє умові .

Обернена заміна дає:

Відповідь: 2.

Приклад 8. Розв’яжіть систему рівнянь

Розв’язання. Заміна 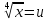і дає систему

З перøого рівняння цієї системи:

Тоді з другого рівняння одержуємо

Звідси 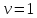, тоді .

Обернена заміна дає:

Відповідь: (16;1)

Ми знаємо, що сторонні корені рівняння можна виявити в результаті перевірки.

Коли йдеться про перевірку як про етап розв’язування рівняння, неможливо уникнути проблеми її технічної реалізації. Наприклад, число є коренем рівняння Щоб у цьому переконатися треба провести значну обчислювальну роботу.

Для подібних ситуацій можливий інший шлях розв’язування – метод рівносильних перетворень.

Теорема 3. Рівняння виду рівносильне системі

Доведення. Нехай число α є коренем даного рівняння. Тоді Звідси Обидві частини числової рівності піднесемо до квадрата. Отримаємо правильну числову рівність . Таким чином, число α є розв’язком системи.

Нехай число β є розв’язком системи, тобто

Звідси отримуємо, що З того, що невід’ємні числа рівні,випливає, що . Отже, число β є коренем даного рівняння.

Таким чином, кожний розв’язок рівняння даного рівняння є розв’язком системи, і навпаки. Отже, множини розв’язків рівняння і системи рівні.

Зауваження. Зрозуміло, що рівняння також є рівносильне системі

Приклад 9. Розв’яжіть рівняння

Розв’язання. Дане рівняння рівносильне системі

Звідси

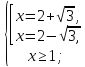
Відповідь.

Теорема 4. Рівняння виду рівносильне системі

Приклад 10. Розв’яжіть рівняння

Розв’язання. Дане рівняння рівносильне системі

Звідси

Відповідь: .

Теореми 3 та 4 можна узагальнити, керуючись таким очевидним твердженням: якщо і то з рівності випливає, що

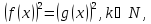Теорема 5. Якщо для будь-якого виконуються нерівності і то рівняння і рівносильні на множині M (Теореми 4 і 5 доводяться відповідно до ідеї доведення Теореми 3).

Приклад 11. Розв’яжіть рівняння

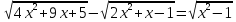
Розв’язання. Вигідно розкласти квадратні тричлени, які стоять під радикалами, на множники:

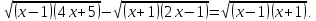
На цьому етапі є дуже поширена помилка: застосування теореми про корінь з добутку у вигляді Наведений запис формули справедливий лише для і а якщо і , то

Оскільки областю визначення даного рівняння є множина (рис. 1), то дане рівняння рівносильне сукупності двох систем і одного рівняння.

1. 

2. 

Зрозуміло, що ця система розв’язків не має.

3. 

Відповідь: -1; 5.

Стандартний метод розв’язання ірраціональних нерівностей полягає в піднесенні обох частин нерівності в потрібну степінь: якщо нерівність під квадратним коренем, то в квадрат; якщо корінь третьої степені – то в куб і та д. Однак, перетворення нерівності, не порушуючи рівносиль ноті, можливо лише нерівності, у яких обидві частини невід'ємні. При піднесенні до квадрата нерівностей, частини яких мають різні знаки, можуть вийти нерівності, як рівносильні вихідному, так і нерівносильні йому. Простий приклад: -1<3 – нерівність правильне, - теж правильна нерівність. Незважаючи на те, що -4 <-1 - нерівність вірна, нерівність вже не є вірним.

Покажемо, як отримати рівносильні системи для деяких часто зустрічних типів нерівностей.

Нерівність виду

Якщо x лежить в ОДЗ: f (x) ≥ 0, то ліва частина нерівності існує і невід'ємна. Оскільки для всіх x, які є розв'язком даної нерівності, права частина більше лівої, то g (x)> 0. Отже, обидві частини нерівності невід'ємні (для тих x, які є розв'язками нерівності, інші x нас не цікавлять). Значить, зведення в квадрат не порушує равносильности і можна записати рівносильну нашому нерівності систему нерівностей:

Приклад 12. Розв’яжіть нерівність

Відразу перейдемо до рівносильної системи:

Відповідь:

Приклад 13. Розв’яжіть нерівність

Перейдемо до рівносильної системи:

Відповідь:

Нерівність виду

ОДЗ даної нерівності f (x) ≥ 0. Нехай для якихось x з ОДЗ g (x) <0. Тоді, очевидно, всі ці x - розв'язки, так як при цих x ліва частина визначена (x ОДЗ) і невід'ємна, в той час як права частина g (x) <0.

Для інших x з ОДЗ g (x) ≥ 0. Для них обидві частини нерівності невід'ємні, і його можна звести в квадрат: Значить, дане нерівність рівносильна сукупності нерівностей:

Зауважимо, що в останню систему не входить вимога f (x) ≥ 0. Воно й не потрібно, так як виконується автоматично бо повний квадрат завжди невід'ємний.

Приклад 14. Розв’яжемо нерівність

ОДЗ нерівність:

1. Якщо , то всі ці x ОДЗ, для яких вірно x <-1, - розв'язання. Таким чином, - перша частина відповіді.

2. Якщо, то обидві частини нерівності невід'ємні, і його можна звести в квадрат. Маємо:

Отримуємо, що розв’язком є всі.

Об’єднавши результати 1 і 2, отримуємо, .

Відповідь: .

Приклад 15. Розв’яжемо нерівність

ОДЗ даної нерівності: Будемо розглядати тільки ці x, інші x не можуть бути рішеннями даної нерівності.

1. Якщо , тобто , то всі такі x з ОДЗ, що задовольняють цій умові, є рішеннями нерівності. Значить, все x ≤ -3 - рішення нерівності.

2. Якщо тобто , а з урахуванням ОДЗ це означає, що то обидві частини нерівності невід'ємні. Зведемо обидві частини нерівності в квадрат:

Рівняння має корені:

і . Отже, розв’язком нерівності є . З урахуванням 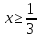виходить, що на даній множині розв’язком є . Об’єднавши результати 1 і 2, отримуємо,

.

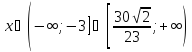Запишемо це розв’язання іншим способом:

Відповідь: .

Нерівність виду

ОДЗ даної нерівності: 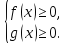Обидві частини нерівності невід'ємні в ОДЗ, і тому можна зводити в квадрат. Отримаємо рівносильну систему

Зауважимо, що з нерівності випливає, що , тобто додатково це вимагати і включати це нерівність в систему не потрібно.

Відзначимо корисне слідство. Припустимо, що ОДЗ нерівності вже знайдено, і ми будемо відбирати розв’язки тільки з ОДЗ (це розумно, оскільки поза ОДЗ розв’язків немає). Тоді вихідна нерівність рівносильне наступному: , а та система, якою це нерівність рівносильно, може бути представлена (для x з ОДЗ) у вигляді . Отже, в ОДЗ

.

Ясно, що ті ж міркування застосовні і для знака нерівності ≥. Звідси можна зробити корисне висновок:

Знак різниці 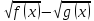збігається зі знаком вираження

Звідси ж виходить ще одна корисна наслідок:

в ОДЗ:

Приклад 16. Розв’яжемо нерівність

ОДЗ даної нерівності:

Зауважимо, що в ОДЗ x ≥ 0, тому існує 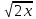і значить

Ми скористалися тут тим, що в ОДЗ x ≥ 0, (x - 5) (x - 6) ≥ 0 і тому існують виписані в останній сходинці корені. Крім того, ми винесли за дужку , який з вищесказаного існує. Цей корінь невід'ємний і тому не впливає на знак нерівності, отже, на нього можна скоротити, не забуваючи, що він може ще перетворитися в нуль і ті x, для яких корінь перетворюється в нуль, є розв'язком нерівності. Таким чином, у відповідь необхідно включити число x = 5. При x = 6 корінь обертається в нуль, але x = 6 не входить в ОДЗ нерівності. Скористаємося тепер тим, що знак різниці коренів збігається зі знаком різниці підкореневих виразів. Маємо:

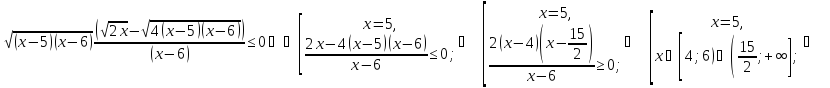
Врахуємо тепер ОДЗ і отримаємо:

Відповідь:

Нерівність виду

ОДЗ даної нерівності: Припустимо, що функції f (x) і g (x) не мають спільних коренів. Розглянемо допоміжну нерівність

1. Якщо g (x) <0, то для будь-якого x з ОДЗ виконано

2. Якщо g (x) ≥ 0, то вираз може мати будь-який знак, але вираз завжди строго додатній. Помноживши обидві частини нерівності на строго додатне число не змінюючи знака нерівності, перейдемо до рівносильної нерівності Таким чином, в ОДЗ

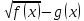Значить, при , знак різниці збігається зі знаком різниці 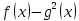в ОДЗ.

Отримуємо наступні умови рівносильності.

Запам'ятовувати наведені системи нерівностей не потрібно, важливо розуміти, як вони виходять.

Приклад 17. Розв’яжемо нерівність .

Виконаємо рівносильні в ОДЗ перетворення і наведемо нерівність до зручного для застосування результатів цього пункту увазі.

Ми не випадково зробили останнє перетворення. Важливо розуміти, чого тут саме дорівнює функція g (x) = 2 x - 8. Типовою помилкою є вважати, що g (x) = 2 x + 8.

ОДЗ даної нерівності: 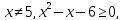тобто 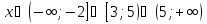Тепер перейдемо до рівносильної системи. В ОДЗ

З урахуванням ОДЗ відразу отримуємо:

Відповідь: