Расчет статистической корреляционной функции случайного процесса

Корреляционная функция (автокорреляционная функция) стационарного случайного процесса g(t) определяется следующим выражением:

. (1)

При значение корреляционной функции равно среднему квадрату случайного процесса

. (2)

Спектральной плотностью случайного процесса называется вещественная функция частоты , определяющаяся выражением:

, (3)

где - изображение Фурье функции .

Дискретные значения корреляционной функции могут быть приближенно определены по формуле

. (4)

Функция называется статистической корреляционной функцией. Она лишь приближенно соответствует действительной корреляционной функции, определяемой формулой (1). В формуле (1) интервал наблюдения, а в реальной выборкевсегда конечно. Чем больше, тем меньше погрешность определения

Рассчитаем статистическую корреляционную функцию случайного процесса. Расчет проведем на ЭВМ. Программа расчета на языкеPASCAL приведена в приложении 2. Результаты вычислений приведены в таблице 3,

Таблица 3

№		№		№		№		№
0	1.145	9	0.17	18	-0.666	27	-0.416	36	0.332
1	1.112	10	0.032	19	0.689	28	-0.331	37	0.375
2	1.043	11	-0.1	20	-0.7	29	-0.242	38	0.406
3	0.951	12	-0.221	21	-0.701	30	-0.15	39	0.422
4	0.843	13	-0.332	22	-0.687	31	-0.057
5	0.721	14	-0.429	23	-0.661	32	0.038
6	0.592	15	-0.509	24	-0.619	33	0.128
7	0.455	16	-0.572	25	-0.564	34	0.208
8	0.312	17	-0.624	26	-0.495	35	0.274

Аппроксимация статистической корреляционной функции

Другой важной характеристикой случайного процесса является его математическое ожидание (среднее значение). Оценка математического ожидания процесса по его выборке определяется по формуле

. (5)

Для аппроксимации статистической корреляционной функции выберем следующее выражение :

, (6)

Необходимо определить параметры .ОчевидноRo=. Пусть первое пересечение графикомоси абсцисс происходит в точке. Тогда, откуда следует. Для определениявыберем произвольную точкуm на начальном участке кривой. Пусть координаты точкиmсоответственно равны (,). Подставим

эти координаты в формулу аппроксимирующей функции :

Из последнего уравнения следует :

.

Ro ==1,145.

=0,157

.==0,0466

Таким образом, получили аппроксимирующую функцию :

=1,145

График этой функции приведен на рис.1

Хорошее совпадение экспериментальной и аналитической кривых вероятно только на начальном участке значений аргумента до , начиная с которого,выходит за пределы (0,3-0,5), так как график, полученный обработкой некоторой реализации конечной длительности, содержит элемент случайности, который может оказать существенное влияние при больших.

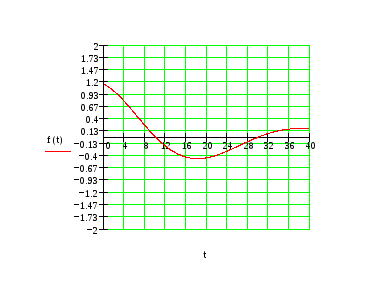
Рис.1

Графики функций и, вычерченные в одних и тех же координатах представлены на Рис.2

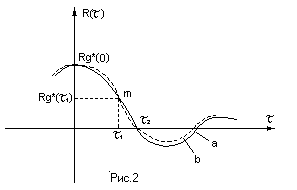
Рис.2 а) Статистическая корреляционная функция

б) ее аппроксимация