
- •Министерство инфраструктуры Украины
- •Содержание
- •Введение
- •1. Назначение, структура и классификация корректирующих кодов
- •1.1 Корректирующие коды в телекоммуникационных системах
- •1.2. Классификация корректирующих кодов
- •Контрольные вопросы
- •Задания
- •2. Параметры блоковых корректирующих кодов
- •Контрольные вопросы
- •3. Способность блоковых кодов обнаруживать и исправлять ошибки
- •Контрольные вопросы
- •Задания
- •4. Алгебраическое описание блоковых кодов
- •Контрольные вопросы
- •Задания
- •5. Кодирование и декодирование блоковых кодов
- •5.1. Кодирование и декодирование блоковых кодов
- •5.2. Синдромное декодирование блоковых кодов
- •5.3. Мажоритарное декодирование блоковых кодов
- •Контрольные вопросы
- •Задания
- •6. Границы параметров блоковых кодов
- •6.1 Верхняя граница Хемминга
- •6.2. Нижняя граница Варшамова-Гилберта
- •6.3 Сложность реализации алгоритмов кодирования и декодирования
- •Контрольные вопросы
- •7. Важные классы блоковых корректирующих кодов
- •7.1. Коды Хемминга
- •7.2. Циклические коды
- •Контрольные вопросы
- •Задания
- •8. Помехоустойчивость декодирования блоковых кодов
- •8.1. Помехоустойчивость декодирования блоковых кодов
- •8.2. Энергетический выигрыш кодирования
- •Контрольные вопросы
- •Задания
- •9. Структура и характеристики сверточных кодов
- •9.1 .Методы описания сверточных кодов
- •9.2. Основные параметры и классификация ск
- •Контрольные вопросы
- •Задания
- •10. Алгоритмы декодирования сверточных кодов
- •10.1. Классификация алгоритмов декодирования
- •10.2. Алгоритм Витерби для декодирования сверточных кодов
- •Контрольные вопросы
- •Задания
- •11. Помехоустойчивость декодирования сверточных кодов
- •Контрольные вопросы
- •Задания
- •12. Критерии эффективности и пути повышения эффективности цифровых телекоммуникационных систем
- •12.1. Теория эффективности а.Г. Зюко.Информационная, энергетическая и частотная эффективности телекоммуникационных систем
- •12.2. Предельная эффективность телекоммуникационных систем и граница к. Шеннона
- •12.3. Перспективные пути дальнейшего повышения эффективности телекоммуникационных систем
- •13. Перспективные методы кодирования в цифровых телекоммуникационных системах
- •13.1.Сигнально-кодовые конструкции
- •13.2. Перспективные методы корректирующего кодирования
- •13.3. Пространственно-временное кодирование
- •13.4. Применение корректирующих кодов в телекоммуникационных системах
- •Приложения а. Характеристики корректирующих кодов
- •А.2. Энергетический выигрыш при использовании циклических кодов
- •А.3. Характеристики двоичных сверточных кодов
- •Б. Методические указания и задание на выполнение курсовой работы
- •Введение
- •В. Перечень знаний и умений, которые должен приобрести студент в процессе изучения материалов модуля 4
- •Г. Примечательные вехи в развитии теории электрической связи
- •Д. Видные ученые, внесшие важный вклад в становление и развитие теории связи х. Найквист (h. Nyquist)
- •К. Шеннон (Claude e. Shannon) (1916-2001)
- •Котельников Владимир Александрович (1908-2005)
- •Зюко Андрей Глебович (1918 – 1998)
- •Литература
- •Помехоустойчивое кодирование в телекоммуникационных системах
Контрольные вопросы
9.1. Назовите основные параметры сверточных кодов.
9.2. Каковы правила построения диаграммы состояний СК?
9.3. Какова связь между диаграммой состояний СК и решетчатой диаграммой?
9.4. Как определить свободное расстояние СК по диаграмме состояний?
Задания
9.1. Заданы порождающие многочлены СК (g(1), g(2)) = (1101,1111). определите параметры такого СК. Каково восьмеричное и многочленное представления (g(1)(D), g(2)(D)) этого кода?
9.2. Приведите функциональную схему кодера из задания 9.1.
9.3. Постройте диаграмму состояний и решетчатую диаграмму кода из задания 9.1. Покажите, как по ним определить свободное расстояние кода. отыщите строку, соответствующую этому коду в таблицах СК приложения А.3. По аналогии с упражнением 9.1 проанализируйте взаимосвязь параметров этого кода с величиной свободного расстояния. Сделайте обобщающие выводы.
9.4. Подготовьте решетчатую диаграмму кода (1, 5) из упражнения 9.1, необходимую для иллюстрации алгоритма Витерби.
10. Алгоритмы декодирования сверточных кодов
10.1. Классификация алгоритмов декодирования СК [1, разд. 10.12; 2, разд. 3.6].
10.2. Алгоритм А. Витерби для декодирования сверточных кодов [2, разд. 3.6].
10.1. Классификация алгоритмов декодирования
При оптимальной обработке с целью вынесения решения принятую из канала последовательность символов необходимо сопоставить со всеми возможными передаваемыми последовательностями. Так как число возможных последовательностей длины N двоичного кода равно 2n, то при больших длинах последовательностей декодер становится недопустимо сложным (экспоненциальная сложность декодирования, см. разд. 6.3), а оптимальное декодирование – практически трудно реализуемым. Однако, именно при больших n возможно значительное повышение надежности передачи, так как действие шума усредняется на длинной последовательности. Поэтому важной является проблема снижения сложности алгоритмов декодирования СК. Известны две группы методов декодирования сверточных кодов:
1) Алгебраические методы декодирования основаны на использовании алгебраических свойств кодовых последовательностей. В ряде случаев эти методы приводят к простым реализациям кодека. Такие алгоритмы являются неоптимальными, так как используемые алгебраические процедуры декодирования предназначены для исправления конкретных (и не всех) конфигураций ошибок в канале. Алгебраические методы отождествляют с поэлементным приемом последовательностей, который для кодов с избыточностью, как известно, дает худшие результаты, чем «прием в целом». Наиболее простым из алгебраических алгоритмов является алгоритм порогового декодирования сверточных кодов. Этот алгоритм далек от оптимального и поэтому редко используется, а используется, в первую очередь, в системах с высокой скоростью передачи информации. Более подробное описание порогового алгоритма и его модификации можно найти в литературе [2, разд. 3.6.3].
2) Вероятностные методы декодирования значительно ближе к оптимальному «приему в целом», так как в этом случае декодер оперирует с величинами, пропорциональными апостериорным вероятностям, оценивает и сравнивает вероятности различных гипотез и на этой основе выносит решения о передаваемых символах.
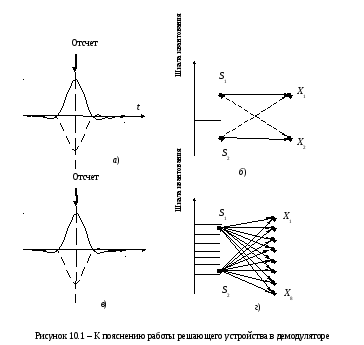
Алгебраические алгоритмы оперируют с конечным алфавитом входных данных, для получения которых на выходе непрерывного канала необходимо выполнить квантование принимаемого сигнала с шумом. Процессы обработки сигналов в решающем устройстве на выходе демодулятора противоположных сигналов показаны на рис. 10.1, где представлены:
а, в) – формы противоположных сигналов в момент отсчета на входе решающего устройства демодулятора.
б) – шкала квантования и граф переходов при жестком решении.
г) – шкала квантования и граф переходов при мягком решении.
В простейшем случае производят квантование каждого канального символа в отсчетный момент времени на два уровня (именуемое в литературе как «жесткое решение» на выходе демодулятора). При жестком решении число уровней квантования L = 2. При этом жесткое решение представлено одним двоичным символом. Это показано на рис. 10.1,б.
При «мягком решении» число уровней квантования L > 2 (рис. 10.1, г).
При мягком решении выход квантователя более точно описывает величину отсчета сигнала с помехой, что повышает помехоустойчивость декодирования.
Известны два основных вероятностных алгоритма декодирования сверточных кодов, а также их различные модификации.
1. Алгоритм последовательного декодирования обеспечивает произвольно малую вероятность ошибки при ненулевой скорости передачи сообщений по каналу. При последовательном декодировании производится поиск пути на кодовой решетке, соответствующего переданной информационной последовательности. Последовательное декодирование используется для декодирования длинных сверточных кодов. Детальное изложение алгоритма последовательного декодирования представлено в литературе [4, разд. 13.18].
Другой разновидностью вероятностных алгоритмов является алгоритм, основанный на принципе динамического программирования, и известный как алгоритм Витерби.
Принцип динамического программирования был сформулирован в 1940 г. Р. Беллманом. С тех пор он нашел широкое приложение в теории управления и теории цепей. В 1970 г. динамическое программирование, в форме алгоритма декодирования СК (алгоритма Витерби), было применено А. Витерби к проблемам телекоммуникации.
2. алгоритм Витерби находит широкое применение и реализует поиск максимально правдоподобного пути на кодовой решетке с отбрасыванием части наименее правдоподобных вариантов путей на каждом шаге декодирования. Алгоритм Витерби характеризуется постоянством вычислительной работы, однако сложность декодера Витерби растет, как при всех переборных алгоритмах, по экспоненциальному закону от длины кодового ограничения сверточного кода. Поэтому алгоритм Витерби используется для декодирования коротких сверточных кодов.
