Свойства спектральной плотности[править|править вики-текст]
Энергетический спектр стационарного процесса (вещественного или комплексного) – неотрицательная величина:
|
|
(7) |
.Энергетический спектр вещественного стационарного в широком смысле случайного процесса есть действительная и четная функция частоты:
|
|
(8) |
.Корреляционная функция
и
энергетический спектр
стационарного
в широком смысле случайного процесса
обладают всеми свойствами, характерными
для пары взаимныхпреобразований
Фурье. В частности, чем «шире»
спектр
тем
«уже» корреляционная функция
,
и наоборот. Этот результат количественно
выражается в виде принципа или соотношения
неопределенности.
20
Квантова́ние — разбиение диапазона значений непрерывной или дискретной величины на конечное число интервалов. Существует также векторное квантование разбиение пространства возможных значений векторной величины на конечное число областей. Простейшим видом квантования является деление целочисленного значения на натуральное число, называемое коэффициентом квантования.
Однородное
(линейное) квантование —
разбиение диапазона значений на отрезки
равной длины. Его можно представлять
как деление исходного значения на
постоянную величину (шаг
квантования)
и взятие целой части от частного:
.
Квантование по
уровню —
представление величины отсчётов
цифровыми сигналами. Для квантования
в двоичном коде диапазон напряжения
сигнала от
до
делится
на
интервалов.
Величина получившегося интервала (шага
квантования):
MY=[x1 x2 x3 x4 y];
tmax(MY,60,4)
function [tmax,delta]=tmax(MX,n,m)
tmax=zeros(m+1,1);
zk=[MX(:,1) MX(:,m+1)];
R=covf(zk,n-1);
Ryy=R(1,:);
plot(Ryy)
tmax(1)=0;
for i=1:n-1
if abs(Ryy(i)>=0.05*Ryy(1))
tmax=i;
end;end;
for k=1:m
zk=[MX(:,1) MX(:,m+1)];
R=covf(zk,n-1);
Rxx=R(1,:);
tmax(k+1)=0;
for i=1,n-1
if (abs(Rxx(i)>=0.05*Rxx(1)))
tmax(k+1)=i;
end;end;end;
tomax=max(tmax);
tomin=min(tmax);
t
real=tomax*16;
delta=tomin/10;
treal
delta
tmax(MY,60,4)
treal =912
delta = 0.1000
ans = 57 1 1 1 1
21
Осложняющий фактор при оценке параметров уравнений локального состава, помимо коррелированности параметров, - возможность существования не одного, а нескольких минимумов функции Q. С 1) имеет до трех решений относительно параметров, а для раствора с положительными или смешанными отклонениями от идеальности - одно решение. От одного до трех наборов корней имеют уравнения UNIQAC и Цубоки - Катаямы. Уравнения NRTL и LEMF обнаруживают до пяти наборов параметров, однако при использовании для расчета только данных о предельных коэффициентах активности число наборов меньше - три, если j 2 In Y 0, al 2 In Y 0, и один в остальных случаях
Высокий статистический коэффициент корреляции ( табл. 4.3) указывает на сильную коррелированность явлений плавления и размягчения в этих системах. [6]
Результаты оценки сгш по (3.18) или (4.71) заметно сме-вдаются в случае значительной коррелированности шума на интервале А при попадании в зону определения шума участков пиков. Эти ошибки могут быть уменьшены итеративно в предположении нормального распределения шума. [7]
Оценки характеристик отдельных каналов связи, полученные например, без учета коррелированности входных сигналов, будут характеризовать динамику не изолированных каналов связи двух величин, а отражать также влияние всех остальных сигналов на выходную величину каждого канала объекта. Определение динамических характеристик объекта с упрощенной структурой не представляет затруднений, но погрешности расчетов могут быть недопустимо велики. Поэтому в каждом конкретном случае нужно иметь в виду цель исследования и оценивать, насколько значительны факторы, которыми желательно пренебречь при упрощении структуры объекта. [8]
Средняя ожидаемая эффективность операции осталась неизменной, а риск уменьшился из-за сильной отрицательной коррелированности дополнительной операции О2 по отношению к основной операции. [9]
Как известно, характерным для нормального режима нефтехимических и нефтеперерабатывающих процессов является коррелированность их входов, что в свою очередь приводит к сильной коррелированности самих коэффициентов искомых регрессионных уровней, к большому значению дисперсии предсказания. В таких случаях существенными преимуществами обладает метод главных компонент, свободный от этих недостатков. Поэтому математическая обработка экспериментальных данных при математическом моделировании процесса алкилирования была проведена методом главных компонент. [10]
Достоинством такой схемы является высокая надежность интегрированной системы, а недостатком - возможная коррелированность ошибок оценок, поступающих от ГЛОНАСС / СР8 - приемника на вход второго фильтра Калмана, и необходимость синхронизации измерений ИНС и ГЛОНАСС / СР8 - приемника. [11]
Единственным, но очень важным условием выигрыша в точности является отсутствие или весьма слабая коррелированность погрешностей преобразователей в наборах. [12]
Из структуры приведенных выражений очевидно, что параметрическое смещение ADn3 обусловлено как коррелированностью параметров at ( t) между собой, так и коррелированностью этих параметров со входным сигналом. [13]
Обратим внимание на то, что хотя с помощью обратного преобразования Койка устранена коррелированность регрессо-ров с ошибками, но автокорреляция ошибок приобретает сложную структуру, и устранение ее может оказаться практически невозможным. Так что хотя получаемые таким образом оценки оказываются состоятельными, они обладают всеми теми недостатками, о которых подробно говорилось в гл. [14]
22
23
Была составлена классификация методов оценки информативности
параметров.
Множество существующих методов оценки информативности
параметров можно разбить на две группы по признаку наличия связи с
ошибкой различения - оценивания.
Первую группу методов оценки информативности составляют методы
основанные на принципе: более информативные параметры должны
доставлять наибольшее значение выбранному критерию информативности.
В качестве подобных критериев используются: энтропия, дивергенция, и др.
Существенным недостатком данных методов является наличие связи с
вероятностью ошибки только для ограниченных видов распределений
параметра, чаще всего для гауссовского. К преимуществам следует отнести
возможность получения выражений для линейных преобразований
исходной совокупности признаков.
С теоретической точки зрения вероятность ошибки является
наилучшим показателем информативности параметра.
Ко второй группе методов относится метод оценки информативности
на основе экспериментального оценивания вероятности ошибки.
Интуитивно выбрав набор параметров, строят на их основе алгоритм
различения, оценивания и экспериментально находят ошибки различения -
оценивания. Это метод является гибким и не зависит от вида распределения.
Недостатки критерия вероятности ошибки заключаются в том что, за
исключением очень небольшого числа частных случаев, для него не
существует явного математического выражения, кроме того оценка
информативности параметров зависит от построения алгоритма различения,
оценивания. Другой подход к оценке информативности параметров, относящийся
ко второй группе связан с использованием не самой вероятности ошибки, а
ее верхней и нижней границ. Подобный метод не зависит от построения
алгоритма различения, оценивания и позволяет определить
информативность без построения алгоритма различения. оценивания.
25
Метод наименьших квадратов является
одним из наиболее распространенных и
наиболее разработанных вследствие
своей простоты и эффективности методов
оценки параметров линейных эконометрических
моделей. Вместе с тем, при
его применении следует соблюдать
определенную осторожность, поскольку
построенные с его использованием модели
могут не удовлетворять целому ряду
требований к качеству их параметров и,
вследствие этого, недостаточно “хорошо”
отображать закономерности развития
процесса
.
Рассмотрим процедуру оценки параметров линейной эконометрической модели с помощью метода наименьших квадратов более подробно. Такая модель в общем виде может быть представлена уравнением (1.2):
yt = a0 + a1 х1t +...+ anхnt + εt.
Исходными данными при оценке параметров a0 , a1 ,..., anявляется вектор значений зависимой переменнойy= (y1, y2, ... , yT )' и матрица значений независимых переменных
в которой первый столбец, состоящий из
единиц, соответствует коэффициенту
модели
.
Название свое метод наименьших квадратов получил, исходя из основного принципа, которому должны удовлетворять полученные на его основе оценки параметров: сумма квадратов ошибки модели должна быть минимальной.
26
27
Метод группового учёта аргументов(МГУА) — семейство индуктивных алгоритмов дляматематического моделированиямультипараметрических данных. Метод основан на рекурсивном селективном отборе моделей, на основе которых строятся более сложные модели. Точность моделирования на каждом следующем шаге рекурсии увеличивается за счет усложнения модели.
Даны
данные наблюдений:
.
Необходимо построить наилучшую в
определенном смысле модель
.
Выбирается общий вид перебираемых моделей, так называемые опорные функции. Часто используется полином Колмогорова-Габора:
Выбор полиномов обусловлен тем свойством,
что согласно теореме
Вейерштрасса, любую непрерывную
на конечном интервале функцию можно со
сколь угодно высокой точностью представить
в виде полинома определенной степени.
Сложность модели в таком случае
определяется количеством коэффициентов
Используя опорные функции строятся различные варианты моделей для некоторых или всех аргументов. Например строятся полиномы с одной переменной, полиномы со всевозможными парами переменных, полиномы со всевозможными тройками переменных, и т.д, полином со всеми переменными. Для каждой модели определяются её коэффициенты
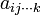методомрегрессионного
анализа.Среди всех моделей выбираются несколько (от 2 до 10) наилучших. Качество моделей определяется коэффициентом детерминации, илисреднеквадратическим отклонениемошибки, иликорреляциейY и исходных данных.
Если найдена достаточно "хорошая" модель или достигнута максимально допустимая сложность моделей, то алгоритм заканчивается.
Иначе, найденные на 3-ем шаге модели используются как аргументы (
)
для опорных функций следующего этапа
итерации (переход на 2-ой пункт). То есть
уже найденные модели участвуют в
формировании более сложных.
Обычно
степень полинома опорной функции
выбирается не выше
,
где
-
количество точек выборки. Часто бывает
достаточно использовать в качестве
опорных функции полиномы второй степени.
В таком случае на каждом шаге итерации
степень результирующего полинома
удваивается.
Вместо полинома Колмогорова-Габораможно использоватьряды Фурье. Их имеет смысл применять, если в исходных данных наблюдается периодичность (например, уровень воды в реках, температура воздуха, объём осадков). Полученная в таком случае модель будет полигармонической[1].
Часто
исходную выборку разбивают на две
подвыборки
и
.
Подвыборка
используется
для определения коэффициентов модели,
а подвыборка
—
для определения качества (коэффициента
детерминацииили среднеквадратического
отклонения). При этом соотношение
количества данных в обеих выборках
может быть как 50%/50% так и 60%/40%.
Статистика показывает, что с каждым шагом итерации уменьшается среднеквадратическое отклонение. Но после достижения определенного уровня сложности (зависит от характера и количества данных, а также общего вида модели), СКО начинает расти.
28
29
Предположим, что матрица системы линейных уравнений и вектор правых частей заданы неточно и вместо предъявленной к решению системы
(30)
в действительности решается некоторая система
,
где
(31)
Обозначим решения
(30) и (31) через 
и
Оценим погрешность
решения 
.
Подставим
выражения 
,
и
в (31)
Вычитая (30), получим
(32)
Если малы 
и
,
то следует ожидать и малости
.
Тогда слагаемое
имеет более высокий порядок малости.
Отсюда следует оценка погрешности
.
(33)
Довольно распространен
случай, когда погрешность матрицы
системы существенно меньше погрешности
правой части; в качестве модели этой
ситуации будем рассматривать случай
точного задания матрицы системы. Тогда,
полагая 
в (33) имеем
(34)
Для качественной характеристики связи между погрешностями правой части и решения вводится понятие обусловленности матрицы системы. Абсолютные погрешности правой части и решения системы зависят от масштабов, которыми измеряется эти величины и матрица системы. Поэтому правильнее характеризовать свойства системы через связь между относительными погрешностями правой части и решения.
Для относительной погрешности решения из (34) имеем
(35)
отсюда 
.
Подставляя оценку
для 
в (35) имеем
(36)
Величину 
называют мерой обусловленности матрицы.
30
Дискретные динамические системы, соответствующие непрерывным системам типа (10 1.19), часто экономно описываются линейным разностным уравнением общего вида
,
(10.2.1)
которое мы будем
называть моделью передаточной функции
порядка
.
Разностное уравнение (10 2.1) можно также
записать при помощи оператора сдвига
назад
в
виде
,
(10.2.2)
или как
.
Точно так же, если
обозначить
,
модель принимает вид
.
(10.2.3)
Сравнив (10 2.3) с (10.1.2), видим, что передаточная функция этой модели равна
.
(10,2.4)
Таким образом,
передаточная функция представима
отношением двух полиномов от
.