3.Этапы решения задачи идентификации:

• по типу объекта: линейные, нелинейные, стационарные, нестационарные, дискретные, непрерывные;

• по типу модели: статические, динамические;

• по обработке экспериментальных данных: постэкспериментальные, в процессе эксплуатации, в процессе проведения эксперимента;

• по способу проведения эксперимента: активные, пассивные.

4. Статическая характеристика элемента - называется зависимость установившихся значений выходной величины от значения величины на входе системы, т.е.:

5. По динамическим характеристикам большинство датчиков относится к усилительным, апериодическим и колебательным звеньям первого и более высоких порядков. Наиболее используемые характеристики датчиков: частотная характеристика и передаточная функция, а параметры - постоянная времени, время запаздывания и коэффициент усиления.

6-8 Этапы решения задачи идентификации:

• по типу объекта: линейные, нелинейные, стационарные, нестационарные, дискретные, непрерывные;

• по типу модели: статические, динамические;

• по обработке экспериментальных данных: постэкспериментальные, в процессе эксплуатации, в процессе проведения эксперимента;

• по способу проведения эксперимента: активные, пассивные.

9. ) Проверка гипотезы о стационарности объекта по критерию серий Вальда-Вольфовица

Дано: выборка значений

Х={х1,…,}, гдеn – измерения;

Определяем медиану значений

Для каждого сигнала вычисляем количество серий: серии последовательности «+» и «–»

если

если

Определяем количество «+» и «–»

Сравниваем

If (V(i).*V(i-1)<0)

Если это условие выполняется, то количество серий увеличивается.

По табл. значениям определяем доверительные точки критерия серий.

Если , то объект стационарен по критерию серий.

Критерий серий Вальда-Вольфовица представляет собой непараметрическую альтернативу t-критерию для независимых выборок. Данные имеют тот же вид, что и в t-критерии для независимых выборок. Данные должны содержать группирующую (независимую) переменную, принимающую, по крайней мере, два различных значения (кода), чтобы однозначно определить, к какой группе относится каждое наблюдение в файле данных.

Критерий серий Вальда-Вольфовица устроен следующим образом. Представьте, что вы хотите сравнить мужчин и женщин по некоторому признаку. Вы можете упорядочить данные, например, по возрастанию, и найти те случаи, когда субъекты одного и того же пола примыкают друг к другу в построенном вариационном ряде (иными словами, образуют серию).

Если нет различия между мужчинами и женщинами, то число и длина «серий», относящиеся к одному и тому же полу, будут более или менее случайными. В противном случае две группы (мужчины и женщины) отличаются друг от друга, то есть не являются однородными.

Критерий предполагает, что рассматриваемые переменные являются непрерывными и измерены, по крайней мере, в порядковой шкале.

Критерий серий Вальда-Вольфовица проверяет гипотезу о том, что две независимые выборки извлечены из двух популяций, которые в чем-то существенно различаются между собой, иными словами, различаются не только средними, но также формой распределения. Нулевая гипотеза состоит в том, что обе выборки извлечены из одной и той же популяции, то есть данные однородны.

Рассмотрим алгоритм на основе критерия серий, который предусматривает построение на основании свойств исходного бинарного ряда наблюдений, принимающего значения только -1 или 1 по правилу:

если

если

где: – медиана исследуемого ряда.

Установлено, что если общее число серий (последовательностей только из подряд идущих 1 или –1) удовлетворяет условию

(где ,- табулированные значения квантилей распределения при заданном критическом уровне значимостии известном объеме наблюдений), то гипотеза о стационарности и независимости случайного процесса принимается. В противном случае принимается гипотеза о наличии тренда процесса.

10. 1) Проверка гипотезы о стационарности объекта по средним значениям и дисперсиям измерений:

Дано:

Х={х1,…,}, где

n – измерение;

Разбиваем последовательность на две части:

Х1={x1,…,}

Х2={,…,}

Определяем среднее значение:

Сравниваем:

- допустимая погрешность, уровень, .

Если это условие выполняется, то объект стационарный, а если не выполняется – то нестационарный. Аналогично и для дисперсии.

11. Т-критерий Стьюдента

Проверка гипотезы о существенности или несущественности различия двух выборочных средних - одна из часто встречающихся процедур в исследовательской работе. В этом случае можно применить критерий Стьюдента (при условии достаточно больших объёмов выборок (n≥30), или убедившись, что статистические ряды близки к нормальному закону распределения). t-критерий применяется в двух вариантах – когда сравниваемые выборки независимы (не связаны) и когда они зависимы (связаны).

Уровень значимости t-критерия равен вероятности ошибочно отвергнуть гипотезу о равенстве выборочных средних двух выборок, когда в действительности эта гипотеза имеет место. При проверке разности двух средних с помощью t-критерия Стьюдента используется следующий алгоритм:

1. Записать вариационный ряд результатов Х экспериментальной группы.

2. Записать вариационный ряд результатов Y контрольной группы.

3. Найти выборочные средние двух выборок и.

4. Найти выборочные дисперсии Dx и Dy.

5. Вычислить эмпирическое значение критической статистики

6. Определить по таблице критическое значение для соответствующего уровня значимостии данного числа степеней свободы.

Если , то различия между средними значениями экспериментальной и контрольной групп существенны на данном уровне значимости, т.е. объект нестационарен и распределен не по нормальному закону распределения.

12.

Для проверки гипотезы поступают следующим образом.

Разбивают всю область значений случайной величины наинтервалови подсчитывают вероятностипопадания случайной величины(т.е. наблюдения) в интервал, используя формулу:

Тогда теоретическое число значений случайной величины , попавших в интервалможно рассчитать по формуле. Таким образом, имеем статистический ряд распределения случайной величины:

			…
			…

и теоретический ряд распределения:

		…
		…

Если эмпирические частоты сильно отличаются от теоретических, то проверяемую гипотезуследует отвергнуть; в противном случае – принять.

Каким критерием, характеризующим степень расхождения между эмпирическими и теоретическими частотами, следует воспользоваться? В качестве меры расхождения между идляК.Пирсон (1857 – 1936; англ. математик, статистик, биолог, философ) предложил величину («критерий Пирсона»):

Согласно теореме Пирсона, при статистика имеетраспределение сстепенями свободы, гдечисло групп (интервалов) выборки,число параметров предполагаемого распределения. В частности, если предполагаемое распределение нормально, то оценивают два параметра (и), поэтому число степеней свободы.

Правило применения критерия сводится к следующему:

По формуле вычисляют выборочное значение статистики критерия.

Выбрав уровень значимости критерия, по таблице- распределения находим критическую точку (квантиль).

Если , то гипотезане противоречит опытным данным: если, то гипотезаотвергается.

Необходимым условием применения критерия Пирсона является наличие в каждом из интервалов не менее 5 наблюдений (т.е. ). Если в отдельных интервалах их меньше, то число интервалов надо уменьшить путем объединения (укрупнения) соседних интервалов.

13. Критерий Шапиро-Уилка

Критерий Шапиро-Уилка используется для проверки гипотезы: «случайная величинараспределена нормально» и является одним наиболее эффективных критериев проверки нормальности. Критерии, проверяющие нормальностьвыборки, являются частным случаемкритериев согласия. Если выборка нормальна, можно далее применять мощные параметрические критерии, например,критерий Фишера.

Описание критерия

Критерий Шапиро-Уилка основан на оптимальной линейной несмещённой оценкедисперсии к её обычной оценке методом максимального правдоподобия. Статистика критерия имеет вид:

где

Числитель является квадратом оценки среднеквадратического отклонения Ллойда.

Коэффициенты берутся из таблиц. Ниже приведена таблица для небольших значений n и i.

Коэффициенты

n	i
	1	2	3	4	5	6	7	8	9	10
3	7071
4	6872	1677
5	6646	2413
6	6431	2806	0875
7	6233	3031	1401
8	6052	3164	1743	0561
9	5888	3244	1976	0947
10	5739	3291	2141	1224	0399
11	5601	3315	2260	1429	0695
12	5475	3325	2347	1586	0922	0303
13	5359	3325	2412	1707	1099	0539
14	5251	3318	2460	1802	1240	0727	0240
15	5150	3306	2495	1878	1353	0880	0433
16	5056	3290	2521	1939	1447	1005	0593	0196
17	4968	3237	2540	1988	1524	1109	0725	0359
18	4886	3253	2553	2027	1587	1197	0837	0496	0173
19	4808	3232	2561	2059	1641	1271	0932	0612	0303
20	4734	3211	2565	2085	1686	1334	1013	0711	0422	0140
21	4634	3185	2578	2119	1736	1399	1092	0804	0530	0263

Критические значения статистики также находятся таблично.

Если , то нулевая гипотеза о нормальности распределения отклоняется при уровне значимостиПриближённая вероятность получения эмпирического значенияпривычисляется по формуле

где — табличные коэффициенты.

Критерий Шапиро-Уилка является очень мощным критерием для проверки нормальности, но, к сожалению, имеет ограниченную применимость. При больших значениях таблицы коэффициентовстановятся неудобными.

14. Критерий Колмогорова для простой гипотезы является наиболее простым критерием проверки гипотезы о виде закона распределения. Он связывает эмпирическую функцию распределения непрерывной случайной величины.

Пусть конкретная выборка из распределения с неизвестной непрерывной функцией распределенияиэмпирическая функция распределения. Выдвигается простая гипотеза:(альтернативная).

Сущность критерия Колмагорова состоит в том, что вводят в рассмотрение функцию

называемой статистикой Колмогорова, представляющей собой максимальное отклонение эмпирической функции распределения от гипотетической (т.е. соответствующей теоретической) функции распределения.

Колмагоров доказал, что при закон распределения случайной величинынезависимо от вида распределения случайной величиныстремится к закону распределения Колмагорова:

где функция распределения Колмагорова, для которой составлена таблица, ее можно использовать для расчетов уже при

	0.1	0.05	0.02	0.01	0.001
	1.224	1.358	1.520	1.627	1.950

Найдем такое, что.

Рассмотрим уравнение С помощью функции Колмогорова найдем кореньэтого уравнения. Тогда по теореме Колмогорова,,, откуда

Если , то гипотезунет оснований отвергать; в противном случае – ее отвергают.

15. Проверка гипотезы про нормальный закон распределения данных по асимметрии и эксцессу

Для проверки гипотезы про нормальный закон распределения данных по асимметрии и эксцессу воспользуемся следующим алгоритмом:

,,

де , ,

критерий λ₀=2,25 для α=0,05.

Приближенные значення средних квадратических отклонений асимметрии и эксцесса:

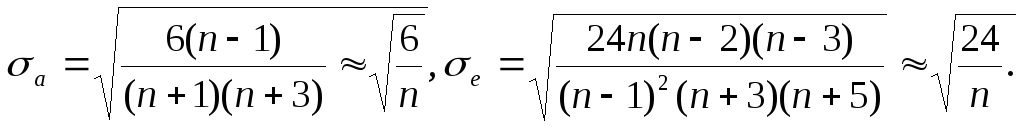
Асимметрия a=m₃/σ³, эксцес e= m₄/σ⁴, ^где

m_х – среднее значение, σ – средне квадратическое отклонения вектора измерений