
Теорема про зміну кінетичної енергії механічної системи
Величина, яка характеризує рух тіла, називається кінетичною енергією. Ця скалярна величина завжди додатна, залежіть тільки від стану механічної системи, і може бути знайдена за наступними правилами.
1.
Якщо тверде тіло здійснює поступальний
рух, то
швидкості
![]() всіх його точок однакові і його кінетична
енергія
всіх його точок однакові і його кінетична
енергія![]() визначається як половина добутку маси
тіла
визначається як половина добутку маси
тіла![]() на квадрат швидкості
на квадрат швидкості
![]() =
=![]() . (1)
. (1)
2.
Якщо тверде тіло обертається навколо
нерухомої осі (наприклад,
![]() )
з кутовою швидкістю
)
з кутовою швидкістю![]() ,
то його кінетична енергія
,
то його кінетична енергія![]() дорівнює половинідобутку
моменту інерції тіла відносно осі
обертання
дорівнює половинідобутку
моменту інерції тіла відносно осі
обертання
![]() на квадрат кутової швидкості
на квадрат кутової швидкості
![]() . (2)
. (2)
3.
Якщо тверде тіло здійснює плоский рух,
то такий рух можна розглядати як
суперпозицію двох простих рухів –
поступального руху центра мас зі
швидкістю
![]() та обертального руху з кутовою швидкістю
та обертального руху з кутовою швидкістю![]() навколо осі, що проходить через центр
мас перпендикулярно площині руху. Тоді
його кінетична енергія
навколо осі, що проходить через центр
мас перпендикулярно площині руху. Тоді
його кінетична енергія![]() визначається як
визначається як
![]() +
+![]() . (3)
. (3)
4. Якщо механічна система складається з декількох тіл, то її кінетична енергія дорівнює сумі кінетичних енергій всіх тіл, що входять в систему, тобто
![]() . (4)
. (4)
Нагадаємо, що розмірністю кінетичної енергії в системі SI є 1 Дж = 1 Н·м.
Робота
є фізична величина яка характеризує
міру передачі руху від одного тіла до
іншого.
Ця фізична
величина теж має розмірність джоуль,
але її величина залежить від процесу
передачі руху, і може бути як додатною,
так і від’ємною. Елементарна робота
![]() сили
сили![]() при елементарному переміщенні матеріальної
точки на
при елементарному переміщенні матеріальної
точки на![]() визначається за правилами скалярного
добутку як
визначається за правилами скалярного
добутку як
![]() =
=![]() ·
·![]() =
=![]() , (5)
, (5)
де
![]() – кут між векторами
– кут між векторами![]() та
та![]() .
Отже, ця величина
.
Отже, ця величина
– додатна, якщо кут між напрямом сили та переміщенням гострий;
– дорівнює нулю, якщо цей кут прямий;
– від’ємна, якщо цей кут тупий.
Робота
сили
![]() при переміщенні
при переміщенні![]() матеріальної точки від точки
матеріальної точки від точки![]() до точки
до точки
![]() визначається інтегралом
визначається інтегралом
![]() =
=![]() . (6)
. (6)
Розглянемо роботу конкретних сил, які можуть діяти в механічній системі.
1.
Робота
сил однорідного поля тяжіння
виконується
силами тяжіння при переміщенні тіла
(матеріальної точки) масою
![]() з початкового в кінцеве положення. Ця
робота не залежить від форми траєкторії,
і визначається лише різницею кінцевого
та початкового
положень тіла вздовж вертикалі. Наприклад,
при переміщенні тіла з положення 1 в
положення 2 (догори) по довільній
траєкторії (рис. 4.1), робота сил тяжіння
визначається як
з початкового в кінцеве положення. Ця
робота не залежить від форми траєкторії,
і визначається лише різницею кінцевого
та початкового
положень тіла вздовж вертикалі. Наприклад,
при переміщенні тіла з положення 1 в
положення 2 (догори) по довільній
траєкторії (рис. 4.1), робота сил тяжіння
визначається як

 ,
(6)
,
(6)
і
буде від’ємною оскільки
![]() >
>![]() .
В таких випадках говорять про виконання
роботи проти сил тяжіння. Навпаки, при
переміщенні тіла з положення 2 в положення
1 (вниз) робота сил тяжіння буде додатною
.
В таких випадках говорять про виконання
роботи проти сил тяжіння. Навпаки, при
переміщенні тіла з положення 2 в положення
1 (вниз) робота сил тяжіння буде додатною
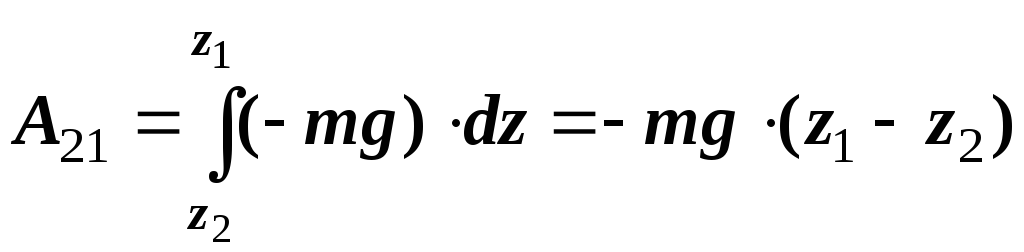 > 0,
> 0,
і говорять про те, що така робота виконана силами тяжіння.
2.
Робота
сили пружності
при розтягуванні (стискуванні) пружини
жорсткістю
![]() від положення
від положення![]() до положення
до положення![]() визначається як
визначається як
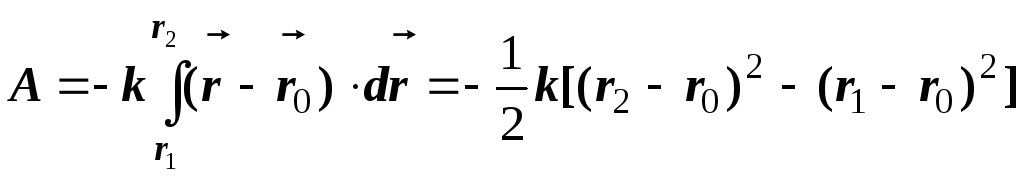 , (7)
, (7)
де
![]() – довжина недеформованої пружини, і
також не залежить від траєкторії точки,
а залежить лише від її кінцевих положень.
– довжина недеформованої пружини, і
також не залежить від траєкторії точки,
а залежить лише від її кінцевих положень.
3.
Робота сил
при повороті тіла
на кінцевий кут при обертанні навколо
нерухомої осі (наприклад,
![]() )
визначається рівнянням
)
визначається рівнянням
![]() , (8)
, (8)
де
![]() – момент зовнішньої сили відносно
нерухомої осі, а
– момент зовнішньої сили відносно
нерухомої осі, а![]() – кут, на який повернулося тіло.
– кут, на який повернулося тіло.
4.
Робота
сил тертя ковзання.
Оскільки сила тертя завжди направлена
в бік, протилежний відносній швидкості
(проти переміщення), то робота сила тертя
визначиться взятому зі знаком мінус
добутку модуля сили тертя
![]() =
=![]() (
(![]() – коефіцієнт тертя ковзання,
– коефіцієнт тертя ковзання,![]() – реакція опори) на довжину траєкторії
– реакція опори) на довжину траєкторії![]()
![]() . (9)
. (9)
5.
Робота сил тертя кочення.
Якщо тіло
котиться без ковзання по поверхні іншого
нерухомого тіла, сила тертя кочення
створює момент
![]() =
=![]() і для роботи сили тертя кочення отримуємо
і для роботи сили тертя кочення отримуємо
![]() , (10)
, (10)
де
–
![]() – коефіцієнт тертя кочення,
– коефіцієнт тертя кочення,![]() – кут, на який повернулося тіло.
– кут, на який повернулося тіло.
Зауважимо, що на відміну від кінетичної енергії системи, яка є функцією стану системи, робота є функцією процесу, які мають місце в системі і між цими величинами існує певний зв’язок.
Якщо
в процесі руху механічна система перейшла
з одного стану, який вона мала в момент
часу
![]() = 0, в інший,
що відповідає моменту часу
= 0, в інший,
що відповідає моменту часу
![]() ,
то можна отримати зв’язок між зміною
кінетичної енергії та роботою сил, які
прикладені до системи
,
то можна отримати зв’язок між зміною
кінетичної енергії та роботою сил, які
прикладені до системи
![]() , (11)
, (11)
де
![]() та
та
![]() – кінетична енергія механічної системи
в кінцевому та початковому станах, а
– кінетична енергія механічної системи
в кінцевому та початковому станах, а![]() – повна робота, яку здійснюють при цьому
переміщенні всі прикладені до системи
внутрішні (
– повна робота, яку здійснюють при цьому
переміщенні всі прикладені до системи
внутрішні (![]() )
та зовнішні (
)
та зовнішні (![]() )
сили.
)
сили.
Рівняння (4.11) є записом теореми про зміну кінетичної енергії в інтегральній формі: зміна кінетичної енергії механічної системи за певний проміжок часу дорівнює сумі робіт внутрішніх та зовнішніх сил, які діють на елементи системи протягом даного проміжку часу.
Відмітимо, що у випадку, коли матеріальна система складається з абсолютно твердих тіл (тобто коли можна нехтувати деформаціями в цій системі), то під дією внутрішніх сил не відбувається зміщень частинок системи, тому сума робіт всіх внутрішніх сил абсолютно твердого тіла при любому його переміщенні дорівнює нулю і теорема про зміну кінетичної енергії набуває вигляду
![]() . (12)
. (12)
