
- •Практическое занятие № 6
- •Основы молекулярно – кинетической теории идеального газа. Законы идеального газа.
- •Основные формулы Идеальные газы подчиняются уравнению состояния Менделеева - Клапейрона
- •1.2. Вопросы для повторения
- •Что надо уметь.
- •Примеры решения задач.
- •Анализ и решение.
- •Анализ и решение.
- •Поэтому дм3.
- •1.5. Задачи для самостоятельного решения
- •Литература
- •Что надо знать.
- •Средняя квадратичная скорость
- •Анализ и решение. Из основного уравнения молекулярно – кинетической теории газов
- •Анализ и решение.
- •Анализ и решение.
- •Анализ и решение.
- •Задачи для самостоятельного решения
- •Литература.
- •3.2. Вопросы для повторения.
- •Что надо знать.
- •Примеры решения задач.
- •3.5. Задачи для самостоятельного решения
- •Литература.
- •Практическое занятие № 9
- •4. Второй закон термодинамики. Энтропия.
- •4.1. Основные формулы
- •4.2. Вопросы для повторения.
- •Что надо знать.
- •Примеры решения
- •4.5. Задачи для самостоятельного решения
- •Литература.
- •5.2. Вопросы для повторения
- •5.3. Что надо знать.
- •5.4. Примеры решения задач.
- •5.5. Задачи для самостоятельного решения
- •Литература.
Что надо знать.
Второй закон термодинамики указывает на необратимость процесса превращения одной формы передачи энергии –работы- в другую форму передачи энергии –теплоту.
В процессах взаимопревращения они не равноценны –количество работы при определенных условиях может быть полностью превращено в тепло, а обратное 100% превращение невозможно.
Примеры решения
Выражая всеобщий закон сохранения и превращения энергии, первое начало термодинамики не позволяет определить направление протекания процессов. Второе начало термодинамики позволяет устанавливать возможное направление самопроизвольных процессов. Исторически открытие второго начала было связано с анализом работы тепловых машин, в частности тепловых двигателей. Обобщение огромного экспериментального материала привело к выводу о невозможности построения вечного двигателя второго рода. Этот вывод получил название второго закона термодинамики.
Существует несколько формулировок второго начала; в соответствии с этим можно записать несколько математических соотношении, выражающих их сущность.
При решении задач используются выражение для коэффициента полезного действия цикла Карно, неравенство Клаузиуса, выражение для изменения энтропии при обратимом процессе и статистическое определение энтропии (формула Больцмана).
Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 7,35*104Дж. Температура нагревателя Т1 = 373 К, температура холодильника Т2 = 273 К. Найти коэффициент полезного действия машины
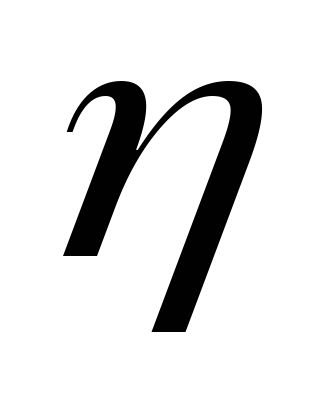 ,
количество теплоты Q1,
получаемое машиной за один цикл от
нагревателя и количество теплоты Q2,
отдаваемое за один цикл холодильнику.
,
количество теплоты Q1,
получаемое машиной за один цикл от
нагревателя и количество теплоты Q2,
отдаваемое за один цикл холодильнику.
Анализ и решение.
КПД идеальной тепловой машины, работающей по циклу Карно:
![]()
Работа совершаемая идеальной тепловой машиной за один цикл, равнa A = Q1 – Q2
С
другой стороны
![]()
Поэтому
Q1
= A/![]() = 7,35*104/0,268
= 27,4*104Дж
= 7,35*104/0,268
= 27,4*104Дж
Тогда Q2 = Q1 – A = (27,4 – 7,35)*104 = 20,05*104Дж
4.4.2.
Тепловая машина работает по обратимому
циклу Карно. Температура нагревателя
Т1
= 500К. Определить термический к.п.д.
![]() цикла и температуру Т2
охладителя тепловой машины, если за
счет каждого килоджоуля теплоты,
полученной от нагревателя, машина
совершает работу А = 350 Дж.
цикла и температуру Т2
охладителя тепловой машины, если за
счет каждого килоджоуля теплоты,
полученной от нагревателя, машина
совершает работу А = 350 Дж.
Анализ и решение.
Термический
к.п.д. тепловой машины, называемый также
коэффициентом использования теплоты,
показывает, какая доля теплоты, полученной
от нагревателя, превращается в механическую
работу. Термический к.п.д. выражается
формулой
![]() = А/Q1,
где Q1
– теплота, полученная от нагревателя,
А – работа, совершенная рабочим телом
тепловой машины
= А/Q1,
где Q1
– теплота, полученная от нагревателя,
А – работа, совершенная рабочим телом
тепловой машины
![]() = 350/1000 = 0,35
= 350/1000 = 0,35
Зная
к.п.д. цикла можно по формуле
![]() =
=![]() .
Определить температуру охладителя Т2
= Т1
(1-
.
Определить температуру охладителя Т2
= Т1
(1-![]() ).
Т2
= 500 (1-0,35)К = 325К.
).
Т2
= 500 (1-0,35)К = 325К.
4.4.3. Какое количество работы следует затратить в идеальной холодильной машине для того, чтобы унести из камеры 1,04*105Дж тепла, если температура в холодильной камере 100С, а температура охлаждающей воды 120С.
Анализ и решение.
Затраченную
работу А/
можно вычислить по формуле Q2
=
![]() ,
где
,
где
![]() -
коэффициент прямого цикла Карно, равный
-
коэффициент прямого цикла Карно, равный![]() .
.
Следовательно
А/
= Q2*![]()
А/
=![]()
4.4.4.
Найти изменение
![]() энтропии
при изобарическом расширении массы m
= 8г гелия от объема V1
= 10л до объема V2
= 25л.
энтропии
при изобарическом расширении массы m
= 8г гелия от объема V1
= 10л до объема V2
= 25л.
Анализ и решение.
Изменение
энтропии определяется формулой
![]()
Изменение энтропии системы при переходе из одного состояния в другое определяется только параметрами этих состояний и не зависит от характера процесса.
Так как процесс равновесный, то интегрирование проводится по любому пути.
Для
изобарного процесса
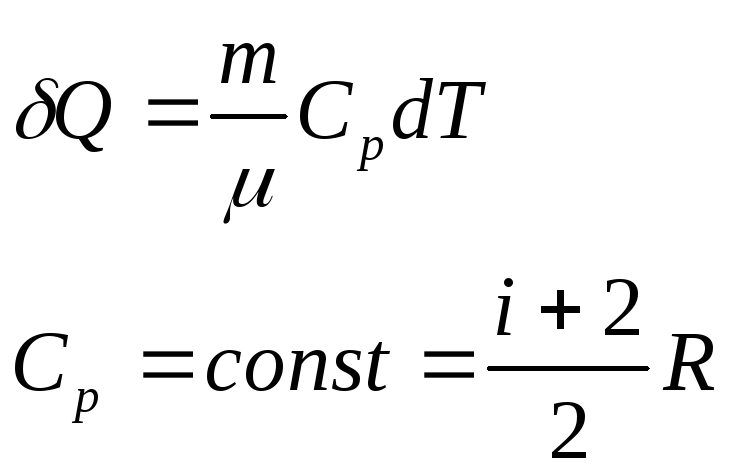
Подставляя
выражение
![]() под
знак интеграла равенства и учитывая
постоянства Сp,
получим
под
знак интеграла равенства и учитывая
постоянства Сp,
получим
![]()
