Связи и их реакции

Тело, перемещению которого в пространстве препятствует какие-нибудь другие тела, скрепленные или соприкасающиеся с данным, называется несвободным. Все то, что ограничивает перемещение данного тела в пространстве, называется связями.

Пример. Груз висит на веревке, ящик стоит на полу и т.д.

Сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям, называется силой реакции (противодействия) связи или просто реакцией связи.

Силы, приложенные к телу, но не являющиеся реакциями, называются активными.

Направление силы реакции связи противоположно той, куда связь не дает перемещаться телу.

Направления реакций некоторых основных видов связи

1. Гладкая поверхность

Реакция связиN гладкой поверхности или опоры направлена по нормали к поверхностям соприкасающихся тел в точке касания и приложена в этой точке.

а) б) в)

Рис. 1.5

Если одна из соприкасающихся поверхностей является точкой, то реакция направлена по нормали к другой поверхности (рис. 1.5).

2. Нить, стержень.

Реакция Т натянутой нити и нагруженного стержняS направлена вдоль этих связей и приложена в точке контакта (рис. 1.6).

а) б)

Рис. 1.6

3. Цилиндрический шарнир (подшипник, петля).

РеакцияR цилиндрического шарнира лежит в плоскости, перпендикулярной оси шарнира, и может иметь любое направление в этой плоскости. Для определения R ее раскладывают на два взаимноперпендикулярных направления: R_x и R_y (рис. 1.7).

Рис. 1.7

4. Подвижная шарнирная опора.

Реакция связиR направлена перпендикулярно плоскости возможного перемещения шарнира (рис. 1.8).

5

Рис. 1.8

а)

б)

Рис. 1.9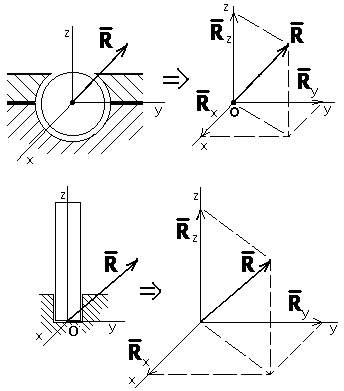

. Шаровый шарнир и подпятник (рис. 1.9, рис. 1.10).

а) б)

Рис. 1.10

Реакция шарового шарнира и подпятника может иметь любое направление в пространстве.

А

Рис. 1.11

а)

б)

ксиома связей. Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей (рис. 1.11).

Сложение сил

Геометрический способ сложения сил

В

а)

б)

Рис. 1.12

еличина, равная геометрической сумме сил какой-либо системы называется главным вектором этой системы сил.

Пусть на твердое тело действует плоская система сил (F₁, F₂, F₃, …, F_n) (рис. 1.12).

Из произвольно выбранной точки О откладывается векторF₁, из его конца откладывается вектор F₂ и т.д. Вектор R, замыкающий силовой многоугольник, является результирующим:

Сложение двух сил

Пусть на тело действуют две силы, лежащие в одной плоскости (рис. 1.13).

.

Р

Рис. 1.13

езультирующая сила определяется по правилу параллелограмма, модуль силы определяется по теореме косинусов или синусов:

; .

Сложение трех сил не лежащих в одной плоскости

Рассмотрим три силы,,не лежащие в одной плоскости (рис. 1.14). Результирующая силаравна:

.

Направление силы определим по направляющим косинусам:

Рис. 1.14

; ; .

Разложение сил

Разложение сил по двум заданным направлениям

Пусть надо силуF разложить по направлениям AB и AD (рис. 1.15).

Рис. 1.15

.

Задача сводится к построению параллелограмма, у которого стороны расположены по направлениям AB и AD и данная сила F является диагональю. Тогда стороны параллелограмма будут искомыми силами.

Разложение сил по трем заданным направлениям.

П

Рис. 1.16

усть направления силы не лежат в одной плоскости. Тогда задача сводится к построению параллелепипеда, у которого диагональю является данная сила, а ребра параллельны заданным направлениям (рис. 1.16).

.

Вопросы для самоконтроля

1. Что изучает статика?

2. Что такое абсолютно твердое тело?

3. Основные виды связей и их реакции?

4. Геометрическое сложение сил?

Задачи, рекомендуемые для самостоятельного решения: 1.1 – 1.6 [2]

Литература: [1], [3], [4].

Лекция 2.

Действия над силами. Система сходящихся сил

Проекция силы на ось и на плоскость

Проекция силы на ось. Пусть сила F образует с осью OX угол  (рис. 2.1), тогда проекция этой силы на ось будет:

F_x = Fcos.

П

Рис. 2.1

роекция силы на ось есть величина скалярная.

Проекция силы на плоскость. Проекцией силы F на плоскость OXY называется вектор F_xy = OB₁, заключенный между проекциями начала и конца силы F на эту плоскость (рис. 2.2.)

П

Рис. 2.2

роекция силы на плоскость есть величина векторная, так как она кроме численного значения характеризуется направлением на плоскости. По модулюF_xy = Fcos, где  - угол между направлением силы F и ее проекцией F_xy.

Аналитический способ задания сил. Для аналитического способа задания силы необходимо выбрать систему координат OXYZ и спроектировать силу на оси координат (рис. 2.3).

Направляющие косинусы определяются по формулам:

Рис. 2.3

; ; .

.

Для плоской системы сил:

; ; ; .