Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Керченский государственный морской технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3й курс 5 семестр / lektsii_po_teor_mekh_-kin_stat.doc

Скачиваний:

584

Добавлен:

08.02.2016

Размер:

3.03 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1819 / 2219 20 21 22 > Следующая >>>

Вопросы для самоконтроля

Определение ускорений точек твердого тела?
Определение углового ускорения твердого тела при плоском движении?

Задачи, рекомендуемые для самостоятельного решения: 18.1 – 18.36 [2].

Литература: [1], [3], [4].

Лекция 12 Сложное движение точки

Если точка движется одновременно по отношению к двум системам отсчета, из которых одна считается условно неподвижной, а другая движется по отношению к первой, то движение, совершаемое при этом точкой, называется составным или сложным.

Например, человек перемещается по вагону поезда (подвижная система отсчета), который движется по отношению к Земле (неподвижная система отсчета).

Рассмотрим сложное движение точки М, перемещающейся по отношению к подвижной системе отсчета ОXYZ, которая в свою очередь как-то движется относительно другой системы отсчета O₁X₁Y₁Z₁ условно названной неподвижной (рис. 12.1).

Рис. 12.1

Движение, совершаемое точкой М по отношению к подвижным осям координат, называется относительным движением. Траектория АВ описываемая в относительном движении называется относительной траекторией. Скорость движения точки М по отношению к осям OXYZ называется относительной скоростью (обозначается ), а ускорение точки в этом движении –относительным ускорением (обозначается ). При вычислениииосиOXYZ можно считать неподвижными.

Движение, совершаемое подвижной системой отсчета OXYZ и всеми неизменно связанными с ней точками пространства по отношению к неподвижной системе O₁X₁Y₁Z₁ является для точки М переносным движением.

Скорость неизменно связанной с подвижными осями OXYZ точки m, с которой в данный момент совпадает движущаяся точка М, называется переносной скоростью точки М в этот момент времени (обозначается ), а ускорение этой точки –переносным ускорением точки М (обозначается ).

На рис. 12.1 АВ – траектория точки М в относительном движении и к ней касательная в этой точке. Поскольку подвижная система координатOXYZ перемещается со скоростью , то результирующей скоростью будет, называемаяабсолютной скоростью, которая является касательной к траектории CD, которая называется абсолютной траекторией. Движение точки М по абсолютной траектории – есть абсолютное движение, а ускорение – абсолютным ускорением.

Сложение скоростей

Теорема. При сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей:

, (12.1)

Рис. 12.2

На рис. 12.2: АВ – траектория точки М в относительном движении;

– относительная скорость точки М;

А₁В₁– положение траектории точки М вследствие переносного движения.

Если угол между исоставляет α, то формула (12.1) в скалярном виде будет:

, (12.2)

Сложение ускорений

Теорема Кориолиса. Абсолютное ускорение точки равно геометрической сумме трех ускорений: относительного, характеризующего изменение относительной скорости в относительном движении; переносного, характеризующего изменение скорости в переносном движении и кориолисово, характеризующего изменение относительной скорости точки в переносном движении и переносной скорости в относительном движении.

, (12.3)

где – кориолисово ускорение.

. (12.4)

Кориолисово ускорение точки равно удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки. Если угол между векторами исоставляет угол α, то модуль кориолисова ускорения будет равен:

. (12.5)

Частные случаи. Кориолисово ускорение будет равно нулю в следующих случаях:

1. Когда , т.е. переносное движение является поступательным, или, если угловая скорость равна нулю;

2. Когда , т.е. когда относительная скорость равна нулю;

3. Когда и, т.е. когда относительное движение происходит по направлению, параллельному оси переносного вращения или, если в данный момент времени векторпараллелен этой оси.

Определение направления кориолисова ускорения (правило Жуковского Е.Н.):

Для определения направления кориолисова ускорения необходимо выполнить следующее:

провести плоскость, перпендикулярную вектору угловой скорости;
спроектировать на эту плоскость вектор скорости в относительном движении;
повернуть проекцию вектора скорости на 90⁰ по ходу вращения переносного движения.

Пример 1.

Точка М в относительном движении из положения движется по диагонали квадратаBCDA по закону , см. КвадратBCDA вращается вокруг неподвижной оси по закону , рад. Сторона квадратаCD = 4см. Определить абсолютную скорость и абсолютное ускорение при t = 1c.

Решение

Рис. 12.3

Определим абсолютную скорость точки М в момент времени t = 1c. Точка М перемещается по диагонали прямоугольника из положения . Так как относительное движение прямолинейное, то скорость точки М в относительном движении будет:

При t = 1c (м/с);м/с.

Вращательное движение точки М вокруг оси ОО₁ является переносным движением. Траектория переносного движения является окружность с радиусом r. Определим положение точки М на прямой АВ при t = 1c.

(см); см.

Из треугольника MDK следует, что

(см);

см.

Так как точка М совершает в переносном движении вращение по окружности с радиусом r, то скорость в переносном движении будет:

где – угловая скорость переносного движения.

;

Тогда

(см/с);

см/с.

Вектор скоростинаправлен по касательной к траектории в точке М, т.е. перпендикулярно плоскости чертежа.

Так как при сложном движении точки:

то вследствие того, что

, тогда см/с.

Абсолютная скорость точки М при t = 1c по модулю равна 43,1 см/с и направлена перпендикулярно плоскости чертежа (на нас).

Определим абсолютное ускорение точки М согласно теоремы сложения ускорений:

Так как в относительном движении точка движется по прямой, то:

При t = 1c, (см/с²);

см/с².

Вследствие движения точки М в переносном движении по окружности (рис. 12.4а):

где – нормальная составляющая ускорения в переносном движении.

(см/с²);

см/с²., вектор нормальной составляющей ускорения направлен по радиусу к оси вращения.

;

– угловое ускорение в переносном движении;

Тогда ;.

Вектор касательной составляющей ускорения направлен в сторону направления вектора скорости (так как движение ускоренное, вследствие того, что ), т.е. перпендикулярно плоскости чертежа (на нас).

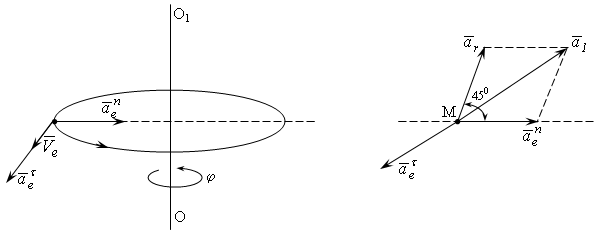
а) б)

Рис. 12.4

Определим кориолисово ускорение:

или в скалярной форме:

где – угол между векторамии.

Так как , то и кориолисово ускорение равно нулю, т.е.:

см/с².

В результате проведенных вычислений установлено, что на точку М в момент времени t = 1c действует три составляющих ускорения: (рис. 12.4б). Векторылежат в плоскости чертежа и угол между ними составляет 45⁰, тогда модуль суммы этих двух векторов будет:

(см/с²);

см/с².

Вектор находится в плоскости чертежа, а вектор– перпендикулярен плоскости чертежа, тогда результирующий вектор – вектор абсолютного ускорения будет:

или в скалярной форме:

(см/с²);

см/с².

Ответ: см/с,см/с².

Пример 2.

Точка М перемещается по окружности диска радиусом R = 2 см по закону из положения А. Диск вращается вокруг неподвижной оси по закону. Определить абсолютную скорость и абсолютное ускорение точки М в момент времениt = 1c.

Решение

Рис. 12.5

R = 2см;

l = 5см.

Анализ характера движения точки М (рис. 12.5) свидетельствует, что движение по окружности диска радиусом R является относительным, а движение диска вокруг неподвижной оси – переносное движение.

Определим положение точки М на окружности диска в момент t = 1c:

(см).

Длина дуги, пройденная точкой М за 1с, составляет см. Определим длину дуги в радианах:

(рад.)

Отсюда следует, что дуга, пройденная точкой М за 1с, составляет рад., или 90⁰ (положение М). Направление вектора скорости будет направлено по касательной к окружности в этой точке (рис. 12.5).

Определим абсолютную скорость точки М в момент t = 1c. По правилу сложения скоростей:

Модуль скорости в относительном движении будет:

; при t = 1c.

(см/с) см/с.

В переносном движении точка М совершает вращательное движение по окружности с радиусом вокруг неподвижной оси (рис. 12.6а).

а) б) в)

Рис. 12.6

Направление вектора переносной скорости перпендикулярно плоскости чертежа в сторону «от нас».

Модуль скорости определим:

где – угловая скорость вращения диска вокруг оси.

; при t = 1c .

Тогда

(см/с);

см/с.

Векторы скоростей иортогональны, так как расположены в двух взаимно пересекающихся плоскостях. Поэтому модуль результирующего вектораопределим:

(см/с);

см/с.

Определим абсолютное ускорение точки М в момент времени t = 1c. Согласно правилу сложения ускорений:

В относительном движении ускорение точки М разложим на две составляющие и, так точка движется по окружности (рис. 12.6б):

где – нормальная составляющая вектора ускорения точки М в относительном движении.

(см/с);см/с.

Вектор направлен по радиусу к центру окружности О.

–касательная составляющая вектора ускорения точки М в переносном движении.

(см/с²); см/с².

Вектор направлен по касательной и окружности и совпадает с направлением вектора скорости, так как движение ускоренное.

Так как в переносном движении точка М движется по окружности вокруг неподвижной оси, то ускорение разложим на составляющие (рис. 12.6а):

где – нормальная составляющая вектора ускорения в переносном движении.

(см/с²); см/с².

Вектор направлен к неподвижной оси.

– касательная составляющая вектора ускорения в переносном движении.

;

– угловое ускорение диска в переносном движении:

(см/с²); см/с².

Вектор направлен перпендикулярно плоскости чертежа и совпадает с направлением вектора скорости переносного движения (так как движение ускоренное).

Определим кориолисово ускорение:

Модуль кориолисова ускорения равен:

где – угол между векторамии.

Согласно «правила буравчика» в данном случае вектор угловой скорости переносного движения направлен параллельно неподвижной оси, вокруг которой вращается диск. Тогда расположение векторов ибудет таким, как представлено на рис. 12.6в. В этом случае вектор кориолисова ускорения, согласно правила Жуковского, будет направлен перпендикулярно плоскости чертежа «на нас».