3.8. Постановка задач оптимальных сау, характеристика получаемых решений. Методы расчетов оптимальных сау.

Оптимальными называются САУ, которые обеспечивают регулирование, доставляющее экстремум показателям качества, например, работа с максимальной производительностью, минимальным потреблением энергии, максимальным к.п.д. и т.д. Указанную суть оптимальных САУ и особенности постановки и решения задач оптимальных САУ рассмотрим на примере нескольких простейших примеров.

1. Задача о кратчайшем расстоянии (min L) между двумя точками (рис.5.1).

Между двумя точками может быть бесконечное множество траекторий (маршрутов), каждой из которых можно сопоставить обобщенную характеристику L – длину траектории. На плоскости (рис.5.1а) ответ очевиден: из всех возможных траекторий1, 2или 3кратчайшей будет прямая линия2. Если между точкамиАиВимеется препятствие, например, холм (рис.5.1б), то очевидно только то, что по прямой линии движение невозможно, а определение кратчайшей линии, которая будет состоять из прямых и криволинейных отрезков, проходящих по склону холма, является сложной для решения задачей.

2. Задача о форме провисающей цепи корабельного якоря, форме провисающих проводов линии электропередачи и т.п. Оказывается, что провисающие якорная цепь, провода и т.п. всегда принимают такую форму, при которой сумма Wпотенциальных энергий элементарных масс цепи или провода принимает минимальное значение (min W), т.е. изменение формы цепи или провода происходит до тех пор, пока это понижает их потенциальную энергию.

3. Задача об управлении электродвигателем по максимуму к.п.д. Необходимо найти такой закон изменения напряжения его питания, чтобы в процессе выполнения заданного объема работы были бы минимальны тепловые потери в его обмотках. Такое управление максимизирует к.п.д.

Решение рассмотренных задач не элементарно, а основано на строгих математических теориях, в которых обязательными компонентами являются аргумент и функция. В математической постановке задач оптимального управления содержание и смысл аргумента и функции отличается от аналогичных понятий, используемых в классической высшей математике. В классической высшей математике связь между аргументом хи функциейуявляется точечной, а именно:числовому значению аргумента сопоставляется числовое значение аргумента в виде аналитической функцииy=f(x). В задачах оптимального управленияаргументом является формула, которая является аналитическим (формульным) описанием траектории (в рассмотренной задаче 1), линии (в задаче 2), закона изменения во времени (в задаче 3) и т.п.Функцией является число(точечное значение), которое является обобщенной характеристикой формульного аргумента: длина пути в задаче 1, потенциальная энергия в задаче 2, величина потерь энергии в задаче 3 и т.п.

Связь между формульным аргументом и числовой функцией называется функциональной связью, а аналитическая запись этой связи называется функционалом.

В качестве функционала чаще всего используют определенный интеграл

(5.1)

Подинтегральное выражение Fявляетсяаргументом функционалаи одновременно функцией от точечных аргументов, например,. Сам же интегралJявляется числом, что подходит под определение функции функционала.

Смысл решения задач оптимального управления состоит в определении такой аналитической зависимости y=f(t), при которой значение функционалаJэкстремально – минимально или максимально. Определенное таким образом решение называетсяэкстремалью. Так, в задаче 1 необходимо найти такое аналитическое описание траектории, у которой длина будет минимальна, в задаче 2 необходимо найти такую форму провисающей цепи, чтобы потенциальная энергия цепи была бы минимальна, в задаче 3 необходимо найти такой закон изменения во времени питающего напряжения, чтобы тепловые потери в электродвигателе были бы минимальны и т.п.

Для решения задач оптимального управления существуют специальные математические методы. Ниже будут рассмотрены два самых распространенных метода: классический вариационный метод и метод принципа максимума Понтрягина.

Основные формулы и теоремы вариационного исчисления

Вариационное исчисление позволяет отыскивать экстремали функционала,

Основной теоремой вариационного исчисления является теорема Эйлера: если функция у=у(t) доставляет экстремум интегралу J, то она должна удовлетворять следующему дифференциальному уравнению (уравнению Эйлера):

(5.2)

Решение уравнения Эйлера называется экстремалью.

Применим уравнение Эйлера для определения формы линии на плоскости (рис.5.1а), которая кратчайшим способом соединяет две точки – АиВ.

Длина элементарного участка траектории согласно рис.5.1а равна

Длина всей линии

. Здесь

Находим частные производные от Fи производную по аргументух

(5.3)

Подставляем (5.3) в уравнение Эйлера (5.2)

,

откуда

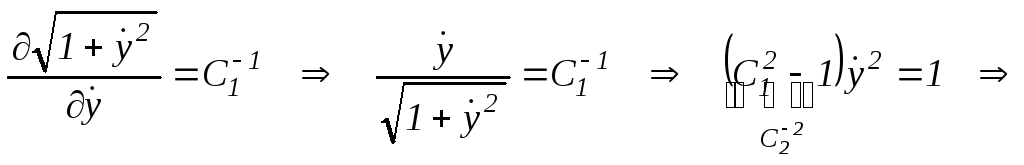
Это уравнение прямой линии, соединяющей точки АиВ. Постоянные интегрирования находятся из условия прохождения прямой чрез точкиАиВ.

В общем случае уравнение Эйлера является дифференциальным уравнением второго порядка, и в решение его входят две произвольные постоянные. Эти произвольные постоянные должны быть определены из граничных условий. Простейшим случаем граничных условий является условие, чтобы кривая у(t) проходила через две заданные точки:.

В частных случаях уравнение Эйлера может превращаться в дифференциальное уравнение 1-го порядка, или даже в уравнение, не содержащее производных. Соответственно должно уменьшаться и число задаваемых граничных условий.

Уравнение Эйлера является необходимым, но не достаточным условием, т.е. функции, удовлетворяющие уравнению (5.2), в некоторых случаях могут не доставлять экстремума. Для того чтобы решения уравнения Эйлера доставляли экстремум функционалу (5.1), достаточно, чтобы они не имели самосопряженных точек (условие Якоби) и выполнялось условие (Лежандра):

- для минимума и- для максимума функционала (5.1).

Задача о разыскании экстремума функционала (5.1) является простейшей задачей вариационного исчисления. Существуют обобщения (варианты) вариационных задач, постановка которых несколько шире простейшей.

Первым обобщением простейшей задачи является пространственная задача, когда функционал зависит от нескольких функций у₁, у₂, …(в классическом понимании), входящих в подинтегральную функциюF(функцияFявляется аргументом функционала)

(5.4)

В этом случае нам нужно найти пфункций отt,т.е.у₁, у₂…у_n,которые при подстановке в (5.4) доставят экстремум функционалуJ. Эти функции находятся из системыпуравнений Эйлера:

Другим (особенно нужным для задач автоматического управления) обобщением простейшей задачи вариационного исчисления является задача на условный экстремум, когда функции y_i(t), входящие в функционал (5.4), должны удовлетворять еще некоторым добавочным условиям. Наиболее общим случаем задачи на условный экстремум является общая задача Лагранжа, когдаnфункцийу₁, у₂,…, у_n, доставляющих максимум функционалу (5.4), удовлетворяют еще системе, состоящей изkинтегральных,mдифференциальных иlалгебраических выражений:

(5.5)

В этом случае составляется mуравнений Эйлера для промежуточной функцииL, определяемой равенством:

(5.6)

где λ₁, λ₂ ,…,λ_k – постоянные числа, а λ_k+1(t),…,λ_k+m+l(t) - произвольные функции отt. Итого для определенияnфункцийуиk+m+lфункцийλ(t) имеем систему изn+m+k+lуравнений:nуравнений Эйлера иk+m+lуравнений (5.6).

Следующим обобщением простейшей задачи вариационного исчислений является задача отыскания экстремума функционала, зависящего не только от первой, но и от старших производных искомой функции:

решение ищем из уравнения Эйлера—Пуассона:

,

которое является в общем случае дифференциальным уравнением порядка 2n. Для полного определения искомой функцииу(t) необходимы2nграничных условий, которые могут быть заданы, например, путем задания значений функцииу(t) и (п-1) ее производных в точкахt₁иt₂.

Самым сложным обобщением простейшей задачи вариационного исчисления является задача, в которой на искомую функцию у(t) накладываются дополнительные ограничения в виде неравенств.

Заданное неравенство или система неравенств ограничивают некоторую область, и искомая функция у(t), доставляющая экстремум, может заключаться только внутри этой допустимой области и не может выходить за ее пределы.

Поэтому при решении этой задачи (называемой часто задачей на ограниченную вариацию) могут встретиться следующие три возможности:

1. Решение уравнения Эйлера целиком находится внутри допустимой области и нигде не выходит за ее пределы. В этом случае искомая функция целиком определяется уравнением Эйлера, и наличие неравенств на решение не влияет.

2. Решение уравнения Эйлера целиком находится вне допустимой области. В этом случае экстремальное значение функционала (5.1) будет достигаться тогда, когда функцией у(t), входящей в (5.1), будет являться граница допустимой области. Решением будет граничная кривая.

3. Решение уравнения Эйлера пересекает границу допустимой области. В этом случае экстремум будет достигаться на кривой, "склеенной" из кусков экстремалей и кусков граничных кривых.

Наиболее сложным для исследования является третий случай. В нем мы должны не только найти уравнения экстремалей и уравнения границы допускаемой области, но и координаты точек "склеивания". Найти эти точки помогает следующая теорема: в точках "склеивания" касательная к экстремали и касательная к граничной кривой должны совпадать.

Наконец, надо отметить, что экстремум может достигаться на "ломаных экстремалях", имеющих точки разрыва в первой или в старших производных. В этом случае в точках разрыва t_iдолжны выполняться условия Вейерштрасса-Эрдмана:

Индекс t_i-0означает, что производные берутся приt, стремящемся кt_iслева, аt_i+0означает, чтоtстремится кt_iсправа. Условия Вейерштрасса-Эрдмана являются теми добавочными условиями, которые позволяют нам найти угол наклона касательных к искомой функцииу(t) в точках излома и тем самым полностью определить ее.

Экстремум может достигаться на разрывных функциях и на функциях, удовлетворяющим неравенствам

(5.7)

Нахождение экстремалей в этом случае методами вариационного исчисления чрезвычайно сложно и часто невозможно. Для решения подобных задач эффективен принцип максимума Понтрягина (см. тему 5.8).