Необходимое и достаточные условия существования экстремумов функции одной переменной

Из теоремы Ферма следует, что если х = х₀ точка экстремума, то производная в этой точке равна нулю

f ^/(x₀) =0.

Следует также отметить, что, иногда, в точке экстремума функция может быть недифференцируемой, т.е. в этой точке производная не существует.

• Необходимое условие существования экстремума функции: если х = х₀ - точка экстремума, то f ^/(x₀) =0 или f ^/(x₀) не существует.

Точки, в которых f ^/(x₀) обращается в нуль или не существует, называется критическими.

• Достаточное условие существования экстремума функции: если функция y=f(x) непрерывна в точке х = х₀ и ее окрестности, дифференцируема в этой окрестности, кроме, быть может, самой точки, и производная 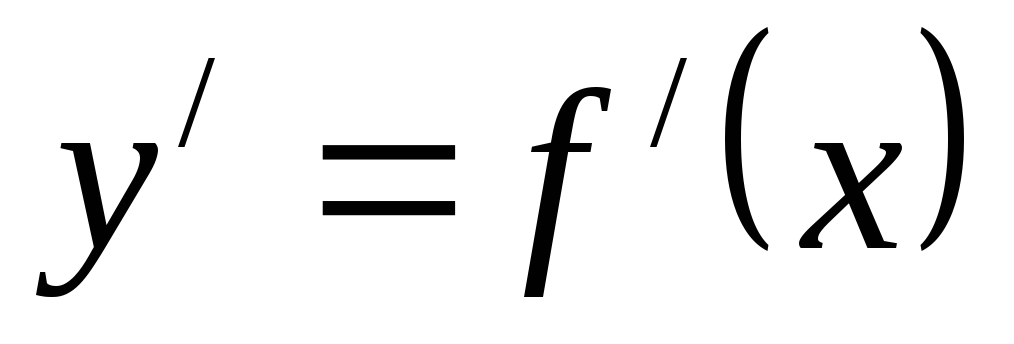при переходе через точку х = х₀ меняет свой знак, то функция имеет экстремум при х = х_{0 .}

При этом х = х₀ - точка максимума, если знак меняется с « + » на « - », и х = х₀ - точка минимума, если знак меняется с « - » на « + » .

2.3.6. Точки перегиба, Выпуклость, вогнутость линии

Дуга кривой называется выпуклой, если она пересекается с любой своей секущей не более, чем в двух точках.Выпуклость дуги может быть направлена или вверх (в направлении оси Оу), или внизЛинии, обращенные выпуклостью вверх, условились называть выпуклыми, а обращенные выпуклостью вниз – вогнутыми.

Необходимое условие выпуклости дуги: есть дуга линии y=f(x) выпукла на (a, b), то при .

Необходимое условие вогнутости дуги: если дуга линии y=f(x) вогнута на (a, b),то при .

Достаточное условие выпуклости, вогнутости дуги: если при, то дуга кривойy=f(x) выпукла на (a, b); если при, то дуга кривойy=f(x) вогнута на (a, b).

Точка С линии, отделяющая выпуклую дугу от вогнутой или наоборот, называется точкой перегиба.

Предполагается, что в точке перегиба можно провести касательную к данной линии, которая лежит при этом по обе стороны от касательной

Cлева от х = х₀ , а справа. Это значит, что слева функцияубывает, а справа возрастает. Интервалы монотонности меняются в точке, в которой производная функция равна нулю или не существует. Точках = х₀ называется при этом критической.

Рассмотренное условие является лишь необходимым условием существования точки перегиба.Достаточное условие существования точки перегиба: если меняет свой знак при переходе через критическую точкух = х₀ , то точка - точка перегиба кривой y = f(x). Знаки слева и справа отх = х₀ показывают, как направлена выпуклость кривой при x < x₀ и x > x₀.

9.6. Асимптоты функции

Если расстояние от точки М линии y=f(x) до прямой l неограниченно уменьшается при неограниченном удалении точки М от начала координат, то такая прямая называется асимптотой линии.

Различают вертикальные и наклонные асимптоты.

1)если х = х₀ – точка разрыва второго рода функции y = f(x), то эта функция имеет вертикальную асимптоту х = х₀ ,в этом случае .

2)если y=kx+b – наклонная асимптота функции y=f(x), то

Чтобы функция y=f(x) имела наклонную асимптоту y=kx+b, необходимо и достаточно, чтобы существовали конечные пределы, определяющие k и b.