9.2. Основные правила и формулы дифференцирования.
Таблица производных.
Процесс нахождения производной называют дифференцированием функции. Пользуясь определением производной и теоремами о пределах, можно вывести правила и формулы дифференцирования основных элементарных функций.
Таблица производных.
Пусть с – постоянная,
u = u(x) и v = v(x) функции.
(с)’ = 0 2. (u + v)’ = u’ + v’
3. (u · v)’ = u’v + u v’, в частности (cu)’ = с · u’
4.
, в частности
5. y = f(u) – сложная функция, где u = u(x), тогда
.
6.
,
,в частности
.
7.
,в
частности
8.
, в частности
.
9.
10.
11.
12.
13.
14.
15.
16.
Показательно-степенная функция
, u
= u(x),
v
= v(x)
равенства
выразить
.
9.3. Дифференциал функции, его свойства.
Пусть дана функция u = f(M) = f(x, y,…,z), D -область определения.
Если координатам
точки М
задать приращения, то получим новую
точку
Полное приращение функции u в точке М (смотри 2.2.1.) :
Главная часть приращения функции
называется полным дифференциалом данной функции u = f(x, y, …,z) в точке M(x, y,…,z) и обозначается
В частности, имеем соответственно
или
для
u
= f(x)
для
u
= f(x,
y)
дляu
= f(x,
y,
z)
Свойства дифференциалов
если С – постоянная величина, то dC= 0;
,
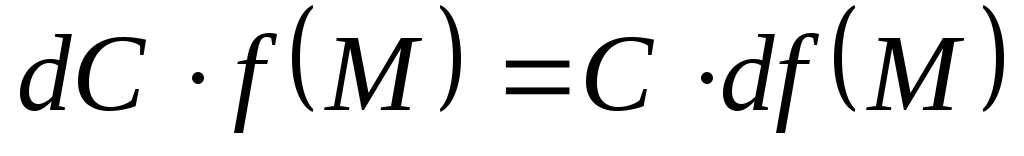т.е. постоянный множитель можно выносить
за знак дифференциала;
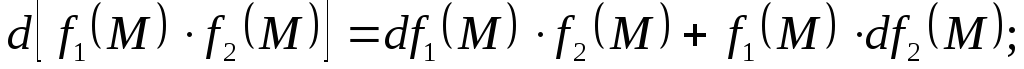
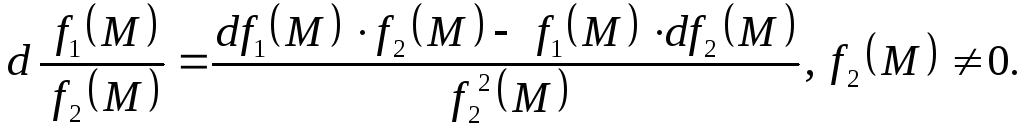
9.4. Основные теоремы дифференциального исчисления
Теорема Ферма.
Если функция y=f(x)
непрерывна в (а,
b),
имеет
экстремум - max
(min)
в некоторой внутренней точке 
и дифференцируема
в этой точке, то ее производная в этой
точке равна нулю:
.
Теорема Роля. Если функция y=f(x) непрерывна на отрезке [a, b], дифференцируема на (a, b) и имеет на концах отрезка равные значения f(a) = f(b)=c , то на интервале (a, b) существует хотя бы одна точка х = х0 такая, что f /(x0) =0
Действительно. Так как функция непрерывна на [a, b], то, по теореме Вейерштрасса (2.1.13) она имеет на этом отрезке наименьшее и наибольшее значения: m и М.
Если m= М, то f /(x0)- const и для любого
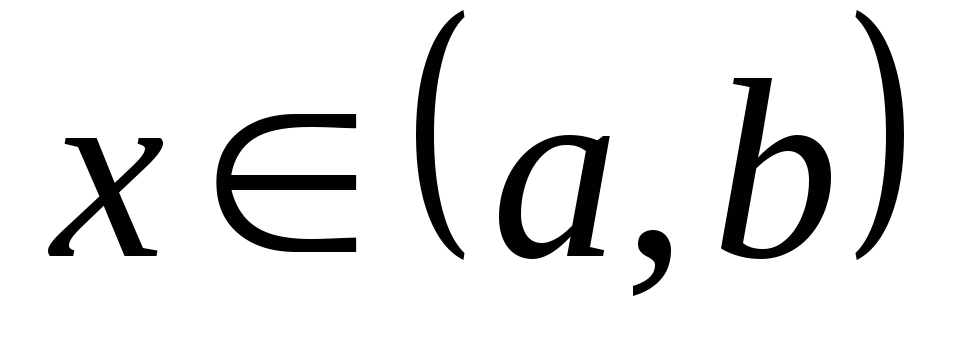имеем f
/(x0)
=0.Если
,то хотя бы одно
из этих значений соответствует внутренней
точке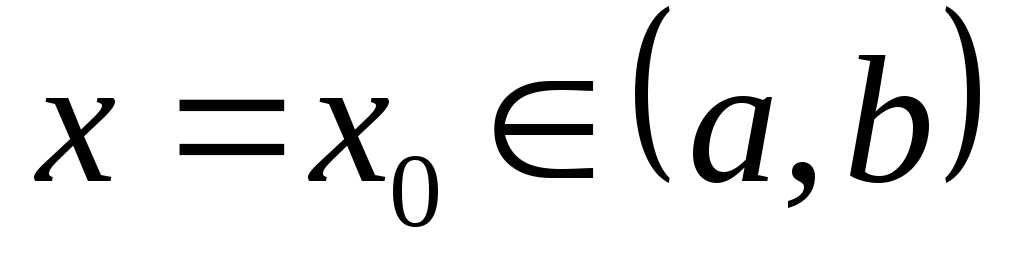 
,но тогда по теореме
Ферма имеем f
/(x0)
=0.
Геометрический смысл теоремы Роля состоит в том, что существует хотя бы одна точка (x0 , f(x0)) такая, касательная в которой к графику функции y=f(x) будет параллельна оси Ох.
Теорема Коши.
Если функция
и 
непрерывны на [a,
b],
дифференцируемы на (a,
b),
причем 
,
то существует хотя бы одна точка 
,
такая, что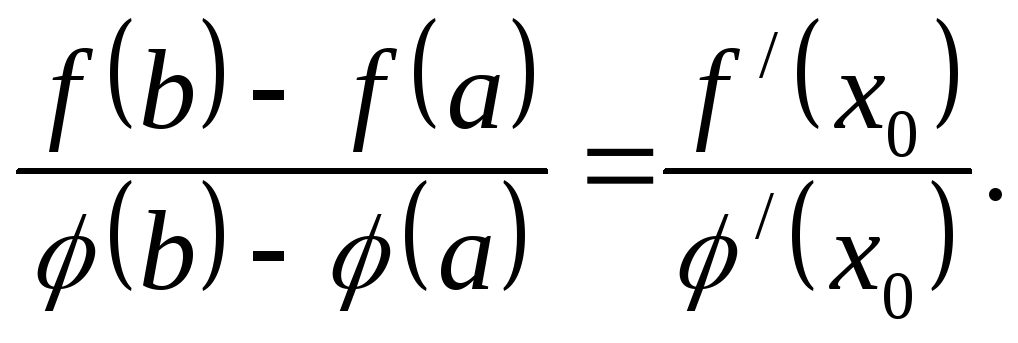 
Теорема Лагранжа.
Если y=f(x)
непрерывна
на [a,
b],
дифференцируема на (a,
b),
то существует хотя бы одна точка 
такая, что 
.
Теорема Лопиталя.
Пусть функции
y=f(x)
и 
в окрестности точки х=
а непрерывны,
дифференцируемы и 
.
При этом при 
или 
одновременно 
или
Тогда, если
существует
,
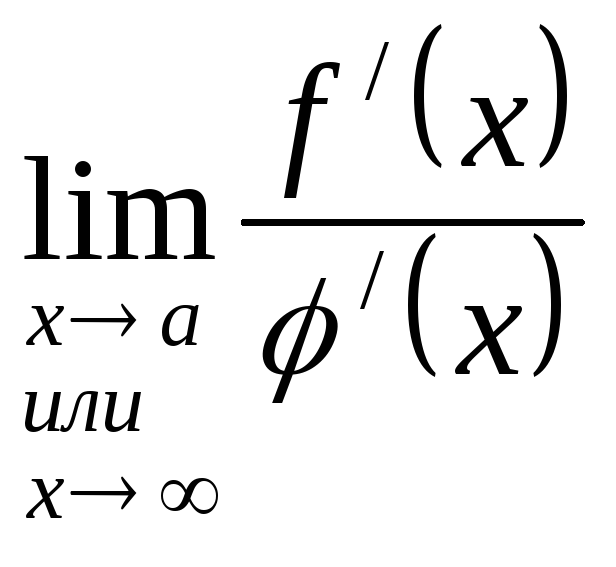то также существует
,
причем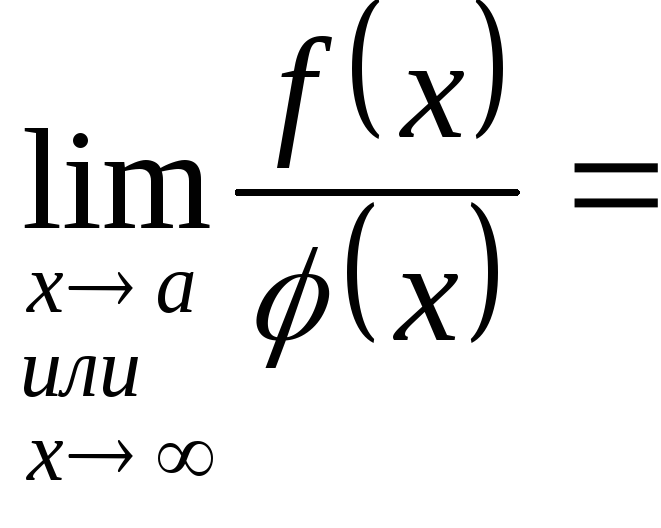
.
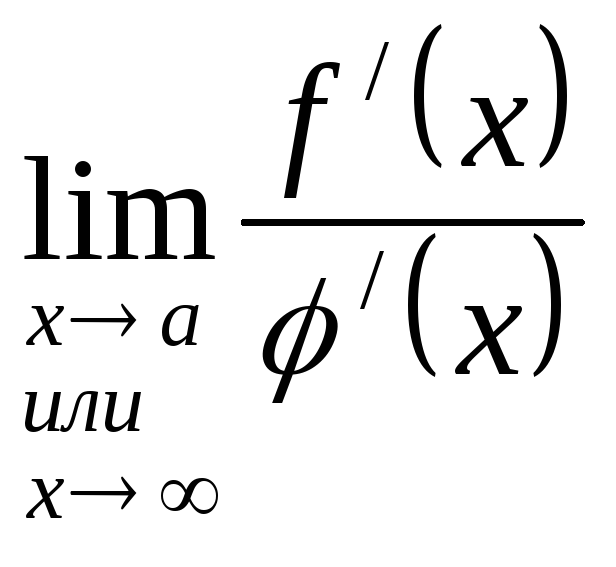9.5. Экстремум функции одной переменной
Рассмотрим следующие виды монотонных функций. Очевидно, что если
1) x1<x2
y1<y2,тогда
y=f
(x)-
возрастающая
функция, 
;
2)x1<x2
y1>y2
тогда
y=f(x)
– убывающая
функция, 
;
3)x1<x2
, 
,тогда y=f3(x)
– неубывающая
функция, в этом случае существует отрезок
[a,
b],
для которого у
сохраняет постоянное значение, 
4) x1<x2
,
y=f
(x)
– невозрастающая функция, существует
определенный
отрезок [c,
d],
для точек которого у
является
постоянным,
.
Необходимые условия монотонности функции:
1)если
функция y=f(x)
возрастает
на (a,
b),
то f
/(x)>0
для 
;
2)
если y=f(x)
- неубывающая
функция на (a,
b),
то 
для
;
3)если
функция y=f(x)
убывает на
(a,
b),то
для 
;
4)
если функция y=f(x)
является невозрастающей на (a,
b),то
для
.