
- •Лекция8 Понятие функции одной и нескольких переменных
- •8.1. Основные элементарные функции, их графики
- •8,5. Бесконечно большие функции одной переменной, их связь с бесконечно малыми.
- •8.6. Теоремы о пределах.
- •Непрерывность функции в точке, на отрезке, в области.
- •Лекция 9 Свойства функций, непрерывных на отрезке
- •9.1. Понятие производной функции в точке.
- •9.2. Основные правила и формулы дифференцирования.
- •9.3. Дифференциал функции, его свойства.
- •9.4. Основные теоремы дифференциального исчисления
- •9.5. Экстремум функции одной переменной
- •Необходимое и достаточные условия существования экстремумов функции одной переменной
- •2.3.6. Точки перегиба, Выпуклость, вогнутость линии
- •9.6. Асимптоты функции
- •2.3.8. Исследование функции одной переменной (общая схема)
- •9.7. Экстремумы функции двух переменных
- •9.8. Формула Тейлора
Лекция8 Понятие функции одной и нескольких переменных
Если каждой точке
![]() по некоторому правилу
по некоторому правилу![]() ставится в соответствие единственное
действительное число
ставится в соответствие единственное
действительное число![]() Ø,
то
Ø,
то![]() называютфункцией,
причем называют D
– область
определения
функции; E
– область
изменения
функции.
называютфункцией,
причем называют D
– область
определения
функции; E
– область
изменения
функции.
Точка
![]() является аргументом функции. Правило
является аргументом функции. Правило![]() ,
однако, применимо не к самой точке, а к
ее координатам.
,
однако, применимо не к самой точке, а к
ее координатам.
Таким образом,
функция
![]() устанавливает связь между точками
устанавливает связь между точками
![]() и точками некоторого множества одномерного
пространства
и точками некоторого множества одномерного
пространства![]() .
.
Область определения
![]() четной
и нечетной
функции симметрична относительно начала
координат. Если это условие не выполнено,
то функция не является четной и не
является нечетной.
четной
и нечетной
функции симметрична относительно начала
координат. Если это условие не выполнено,
то функция не является четной и не
является нечетной.
Функция
 называетсяпериодической,
если существует такое положительное
число Т, что при любом значении
называетсяпериодической,
если существует такое положительное
число Т, что при любом значении
 выполняется равенство
выполняется равенство
![]() ,
,
число Т называют периодом функции.
Функция
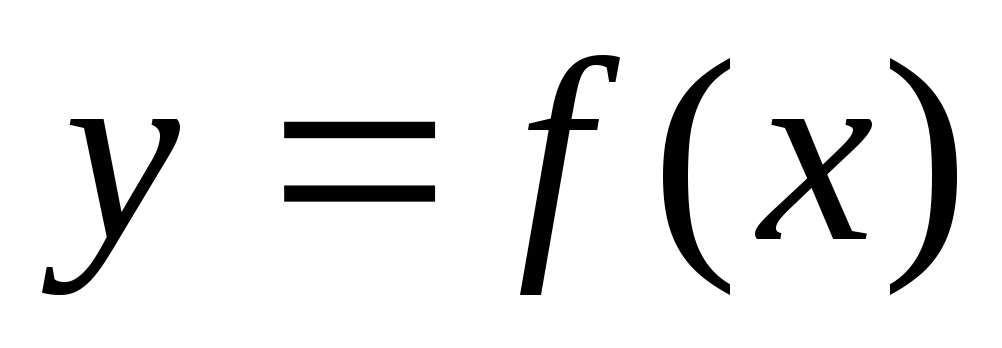 называетсявозрастающей
на множестве
называетсявозрастающей
на множестве
 ,
если большему значению аргумента
соответствует большее значение функции,
то есть для любых
,
если большему значению аргумента
соответствует большее значение функции,
то есть для любых ,
таких, что
,
таких, что ,
выполняется неравенство
,
выполняется неравенство .
.Функция
 называетсяубывающей
на множестве
называетсяубывающей
на множестве
 ,
если большему значению аргумента
соответствует меньшее значение функции:
если
,
если большему значению аргумента
соответствует меньшее значение функции:
если
![]() ,
то
,
то
![]() для любых
для любых![]() .
.
8.1. Основные элементарные функции, их графики
Особую роль в математическом анализе играют элементарные функции.
Основными элементарными функциями называют:
степенную функцию
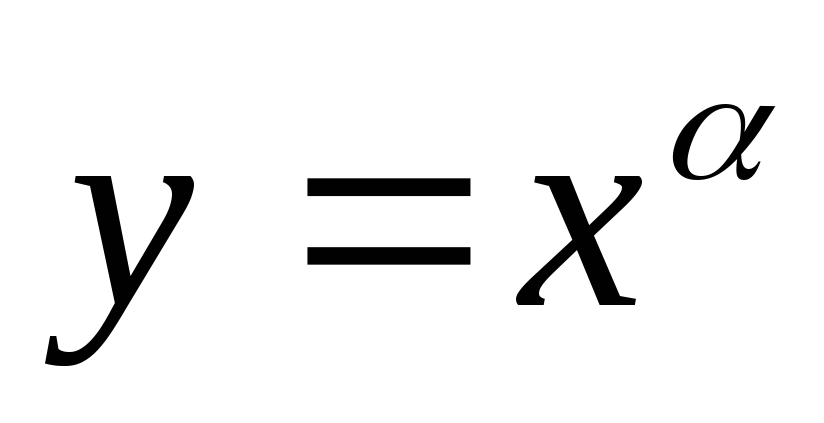 ;
;логарифмическую функцию
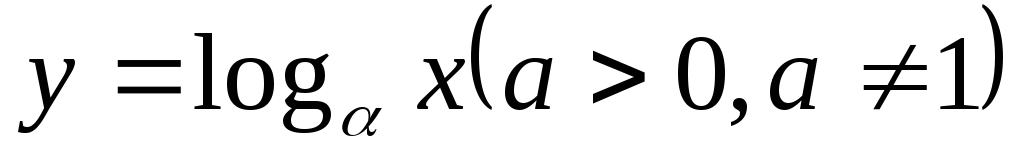 ;
;показательную функцию
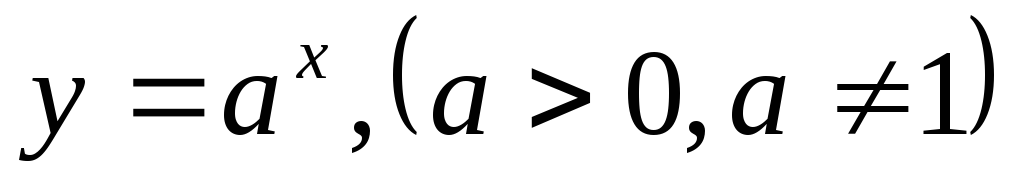 ;
;тригонометрические функции
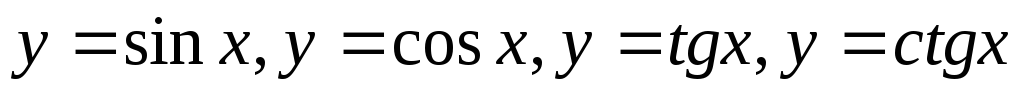 ;
;обратные тригонометрические функции
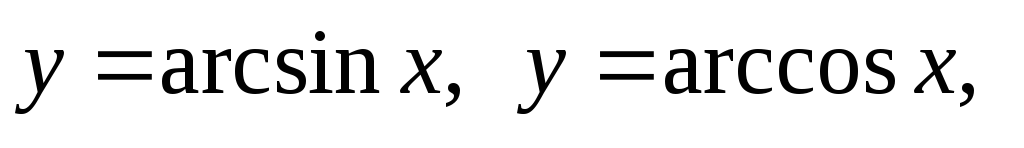

 .
.
Функцию называют элементарной, если ее аналитическое выражение составлено из основных элементарных функций с помощью четырех арифметических действий и операции суперпозиции (функции от функции), примененных конечное число раз.
8.2. Предел функции в точке
Говорят, что ![]() есть предельная
точка
множества
есть предельная
точка
множества
![]() ,
если в любой окрестности этой точки
содержится бесконечное множество точек
,
если в любой окрестности этой точки
содержится бесконечное множество точек![]() .
.
Обозначают
![]() .
.
Используя логические символы данное определение можно записать таким образом:
![]() ,
что для
,
что для
![]() ,
как только
,
как только![]() ,
выполняется
,
выполняется![]() .
.
В частности,
для функции одной переменной
 ;
;
![]() - предельная точка.
- предельная точка.
Определение предела
![]()
можно записать таким образом:
![]() ,
что для
,
что для
![]() :
как только
:
как только![]() выполняется
выполняется![]() ;
;
8.3. Односторонние пределы функции одной переменной.
Теорема существования предела
Предел функции
![]() при
при![]() называетсялевосторонним
и обозначается
называетсялевосторонним
и обозначается
![]() ,если
точка
,если
точка![]() остается все время слева от
остается все время слева от![]() ,
что означает выполнение неравенства
,
что означает выполнение неравенства![]() .
.
Аналогично
определяется и обозначается правосторонний
предел:
![]()
Теорема о существовании предела.
Функция
![]() имеет в точке
имеет в точке![]() предел, равный
предел, равный![]() ,
тогда и только тогда, когда существуют
односторонние пределы в точке
,
тогда и только тогда, когда существуют
односторонние пределы в точке![]() ,
и они равны между собой и равны числу
,
и они равны между собой и равны числу![]() .
.
8.4. Бесконечно малые функции, их классификация
Важное значение в дальнейшем имеют функции, пределы которых в точках равны нулю.
Функция
 называетсябесконечно
малой в точке
называетсябесконечно
малой в точке
 ,
если
,
если .
.Классификация бесконечно малых функций
Если
![]() ,
причем
,
причем![]() и
и![]() то
то![]() и
и![]() называютсябесконечно
малыми одного порядка малости (скорости
приближения
называютсябесконечно
малыми одного порядка малости (скорости
приближения
![]() и
и![]() к нулю являются почти равными).
к нулю являются почти равными).
Если
![]() ,
то
,
то![]() - бесконечно малаяболее
высокого порядка
малости,
чем
- бесконечно малаяболее
высокого порядка
малости,
чем
![]() (
(![]() приближается к нулю быстрее, чем
приближается к нулю быстрее, чем![]() ).
Обозначают
).
Обозначают![]() .
.
Если![]() ,
то
,
то![]() и
и![]() называютсяэквивалентными
бесконечно малыми в окрестности точки
М0
(
называютсяэквивалентными
бесконечно малыми в окрестности точки
М0
(![]() и
и![]() приближаются к0
с одной скоростью). Обозначают:
приближаются к0
с одной скоростью). Обозначают:
![]() ~
~
![]() .
.
