
Методичка 1807
.pdf1
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ Запорізький національний технічний університет
МЕТОДИЧНІ ВКАЗІВКИ ТА ІНДИВІДУАЛЬНІ ЗАВДАННЯ
до контрольної роботи з дисципліни “Вища математика” для студентів економічних спеціальностей заочної форми навчання
Частина 2
2006
2
Методичні вказівки та індивідуальні завдання до контрольної роботи з дисципліни “Вища математика” для студентів економічних спеціальностей заочної форми навчання. Частина 2. / Укл.: Н.О. Нечіпоренко, М.О. Щолокова, О.А. Тиха - Запоріжжя: ЗНТУ,
2006. – 42 с.
Укладачі: Н.О. Нечіпоренко, доцент М.О. Щолокова, старший викладач О.А. Тиха, асистент
Рецензент: Мастиновський Ю.В., доцент
Експерт: Прушківський В.Г., доцент
Відповідальний за випуск: Мастиновський Ю.В., доцент
Затверджено на засіданні кафедри "Прикладної математики"
Протокол № _10_
від "_14_" __06__ 2006р.
3
ЗМІСТ
С.
РОЗВ’ЯЗОК ТИПОВОГО ВАРІАНТУ………………………4
ІНДИВІДУАЛЬНІ ЗАВДАННЯ…………………………......25
ЛІТЕРАТУРА……………..……………………....................42

4
РОЗВ'ЯЗОК ТИПОВОГО ВАРІАНТУ
Основні правила інтегрування
1)Якщо F'(x) = f (x), то∫ f (x)dx = F (x) + C,
2)∫аf (x)dx = a∫ f (x)dx , де а – постійна величина;
3)∫[f1 (x) ± f2 (x)]dx = ∫ f1 (x)dx ± ∫ f2 (x)dx .
Таблиця основних інтегралів
1. |
∫ xn dx = |
|
|
xn+1 |
|
+ C . |
|||||||
|
|
n + 1 |
|||||||||||
|
|
dx |
|
|
|
|
|
||||||
2. |
∫ |
= ln |
|
x |
|
+ C . |
|||||||
|
|
||||||||||||
|
|||||||||||||
|
|
x |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||
3. |
∫ a x dx = |
a x |
+ C, (a > 0, a ≠ 1). |
||||||||||
ln a |
|||||||||||||
|
|
|
|
|
|
|
|||||||
4.∫ex dx = ex + C.
5.∫sin xdx = − cos x + C.
6.∫cos xdx = sin x + C.
7. |
∫ |
|
dx |
|
|
= tgx + C. |
|
|
|
|
|
||||||||||
cos |
2 |
x |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
8. |
∫ |
|
dx |
|
|
= −ctgx + C. |
|||||||||||||||
|
|
|
|
|
|||||||||||||||||
sin |
2 |
x |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
9. |
∫ |
|
|
dx |
|
|
= |
1 |
ln |
|
|
x + a |
|
+ C. |
|||||||
|
|
|
|
|
|
||||||||||||||||
a |
2 |
− x |
2 |
|
|
|
|
x − a |
|||||||||||||
|
|
|
|
|
|
|
2a |
|
|
|
|||||||||||
10. |
∫ |
|
|
dx |
|
|
= |
1 |
arctg |
x |
+ C,(a ≠ 0). |
||||||||||
a |
2 |
+ x |
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
a |
|
a |
||||||||||||
11. |
∫ |
|
|
|
dx |
|
|
= arcsin x + C, x < a . |
|||||||||||||
|
|
|
a 2 − x 2 |
|
|
|
|
|
|
|
a |
||||||||||
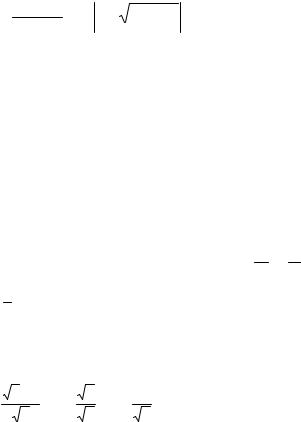
5
12. |
∫ |
x |
2 dx |
|
2 = ln x + |
x2 ± a2 + C. |
|
|
|
|
|
|||
|
|
|
± a |
|
|
|
|
|
|
|
||||
13. |
∫ shxdx = chx + C. |
14. |
∫chxdx = shx + C. |
|||||||||||
14. |
∫ |
dx |
|
|
= thx + C. |
16. |
∫ |
dx |
|
= −cthx + C. |
||||
|
|
|
|
|
|
|
|
|||||||
ch |
2 |
x |
sh |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
x |
||||||
ЗАВДАННЯ 1.
а) Знаходження невизначеного інтеграла шляхом зведення його до табличного називається безпосереднім інтегруванням.
Приклад 1
∫(5x3 +3x2 +4)dx = 5∫ x3dx+3∫ x2dx+4∫dx= 5 x4 +3 x3 +4x +C =
4 3
=5 x4 + x3 +4x +C. 4
Приклад 2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
1 |
|
|
|
|
|
|
1− |
1 |
|
|
|
∫ 3x + 1dx = ∫ 3 |
x dx + ∫ 3dx = ∫ x 6 dx + ∫ x− |
3 dx = |
|
x |
6 |
|
|
+ |
|
x |
3 |
+ C = |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x |
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
1 + |
1 |
|
|
1 − |
1 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
7 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6x 6 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
|
+ |
x |
3 + C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
7 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Приклад 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
∫ |
|
|
cos 2x |
|
|
dx = ∫ |
cos2 x − sin2 x |
∫ |
cos2 x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
dx = |
|
dx − |
|||||||||||||||||||||||||||||||
sin2 xsin2 x |
cos2 xsin2 x |
cos2 xsin2 x |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
sin2 x |
|
|
|
dx |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
− ∫ |
|
dx = ∫ |
|
− ∫ |
|
|
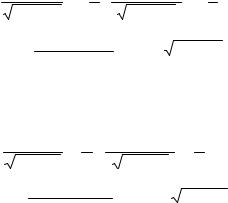
= −ctgx − tgx + C. |
|
|||||||||||||||||||||||||||||||
cos2 xsin2 x |
sin2 x |
cos2 x |
|
||||||||||||||||||||||||||||||||||||
6
б) Заміна змінної в невизначеному інтегралі виконується за допомогою підстановки двох видів:
1) x = ϕ (t) , де ϕ (t) - монотонна, безперервно диференційована
функція нової змінної t. Формула заміни змінної в цьому випадку:
∫f (x)dx = ∫ f [ϕ (t)] ϕ ′(t)dt .
2)u = ψ (t) , де u - нова змінна. Формула заміни змінної при цій підстановці:
∫f [ψ (t)] ψ ′(t)dt = ∫ f (u)du .
Такий варіант заміни змінної часто називають підведенням під знак диференціала. Користуючись цим правилом, можна поширити таблицю основних інтегралів:
15. |
∫tgx dx = ∫ |
sin x |
dx = −∫ |
d(cos x) |
= − ln |
|
cos x |
|
+ C. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
16. |
∫ctgx dx = ∫ |
cos x |
|
dx = −∫ |
d(sin x) |
= ln |
|
sin x |
|
+ C. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Приклад 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− x 2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
∫ |
|
|
xdx |
|
|
|
|
|
= − |
1 |
|
∫ |
d (a 2 |
|
= − |
1 |
∫ (a |
2 |
− x |
2 |
|
− |
1 |
|
|
2 |
− x |
2 |
) = |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
) |
2 d (a |
||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
2 |
|
− |
x |
2 |
|
|
2 |
|
a |
2 |
|
− x |
2 |
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= − |
1 |
(a 2 − x 2 |
) 2 |
+ C = − a 2 − x 2 + C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
1 − |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Приклад 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
∫ |
|
|
xdx |
|
|
|
|
|
= |
1 |
|
|
∫ |
|
d ( x 2 |
+ |
a ) |
= |
1 |
∫ |
|
2 |
+ a ) |
− |
1 |
|
|
|
2 |
+ a ) = |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
( x |
2 d ( x |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
x |
|
|
2 |
+ |
a |
2 |
|
|
|
|
x |
2 |
|
+ |
a |
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
1 |
+ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
= |
1 |
( x 2 |
+ |
a ) 2 |
|
|
+ C = − x 2 + a + C . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
− |
|
+ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Цими інтегралами можна користуватися як табличними.

7
Приклад 6
Знайти |
|
∫ x |
|
|
|
dx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2x − 9 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Нехай |
|
2x − 9 = u2 , тоді |
|
|
|
x = |
u 2 + 9 |
, |
dx = u du. |
||||||||||||||
|
|
|
|
|
|||||||||||||||||||
Маємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∫ |
dx |
= ∫ |
|
|
|
udu |
|
|
= |
2 ∫ |
|
du |
= 2 |
1 |
|
u |
+ C = |
||||||
|
2 |
|
|
2 |
|
|
|
|
|
2 |
|
arctg |
|||||||||||
|
x 2 x − 9 |
|
|
u + 9 |
u |
|
|
u + |
9 |
|
3 |
|
3 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 arctg |
2 x − 9 + C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приклад 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Знайти |
|
∫ |
sin 2xdx . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
3 − cos4 x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Нехай cos2 x = t , тоді |
dt = −2 cos xsin xdx, |
dt = − sin 2xdx. . |
|||||||||||||||||||||
Маємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
sin 2xdx |
= −∫ |
|
dt |
|
|
= − arcsin |
t |
+ C = C − arcsin cos2 x. |
||||||||||||||
|
3 − cos4 |
x |
|
|
|
|
|
3 − t 2 |
|
|
|
|
|
3 |
|
|
|
|
3 |
||||
Приклад 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Знайти |
|
∫ |
|
x4 dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x10 |
− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тому що x4 |
є похідною |
|
1 |
x5 , то замінивши x5 |
на t, отримаємо: |
||||||||||||||||||
|
5 |
||||||||||||||||||||||
|
x 4 dx |
|
|
1 |
dt |
|
|
1 |
|
|
dt |
|
|
|
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∫ |
x10 − 2 = ∫ t52 − 2 = |
5 ∫ |
t 2 − ( 2 )2 |
= |
5 ln t + t 2 − 2 + C = |
||||||||||||||||||
= 1 ln x 5 +  x10 − 2 + C.
x10 − 2 + C.
5

8
в) Інтегрування по частинам.
Якщо u(x) та v(x) диференційовані функції, то правдива наступна формула інтегрування по частинам
∫udv = u v − ∫vdu.
Цією формулою можна користуватися неодноразово. Треба вказати 4 основні випадки, коли використовується метод інтегрування по частинам.
1)Інтеграли виду ∫ Pn (x)ex dx .
Тому що при диференційовані показник ступеня многочлена
Pn (x) |
зменшується, то підінтегральні вирази треба розподілити |
|||
так: |
|
|
|
|
|
|
Pn (x) = u, exdx = dv. |
|
|
Тоді |
du = Pn′(x)dx |
та v = ∫ex dx = ex . |
||
З формули |
∫udv = u v − ∫vdu |
маємо: |
||
|
|
∫ Pn (x)ex dx = Pn (x)ex − ∫ Pn′(x)ex dx. |
||
До інтегралу справа знову використовуємо формулу інтегрування по частинам. Так треба робити доки при
ex множник залишиться постійнім.
Приклад 9 |
|
|
Знайти |
∫ x2 ex dx, |
|
Нехай |
u = x2 та dv = ex dx , |
тоді du = 2xdx та v = ex . |
Зформули інтегрування по частинам маємо:
∫x2 e2 dx = x2 ex − ∫2xex dx.
Для інтегралу ∫2xex dx знову застосуємо формулу: u = x, dv = ex dx du = dx, v = ex ,
∫ x2 ex dx = x2 ex − 2(xex − ∫ex dx) = x2 ex − 2xex + 2ex + C.

9
2) Для інтегралів виду: ∫ Pn (x)sin xdx та ∫ Pn (x) cos xdx
діємо аналогічно, як і в випадку 1).
Приклад 10
Знайти |
∫ x cos xdx. |
Нехай |
u = x та dv = cos xdx , тоді du = dx та v = sin x . |
∫ x cos xdx = x sin x − ∫sin xdx = x sin x + cos x + C.
3)Інтеграли виду: ∫ Pn (x) ln xdx .
В цьому випадку логарифмічну функцію слід прийняти за u, тому що після диференціації вона спроститься:
u = ln x, |
dv = Pn (x)dx, |
||
du = |
dx |
, |
v = ∫ Pn (x)dx . |
|
|||
|
x |
|
|
∫Pn (x) ln xdx = ln x ∫ Pn (x)dx − ∫ 1 ∫ Pn (x)dx dx + C.
x
Приклад 11 |
|
|
|
|||
Знайти |
∫ x ln xdx. |
|
|
|
||
Нехай |
u = ln x , dv = xdx, du = |
dx |
, |
v = |
x2 |
. |
|
|
|||||
|
|
x |
2 |
|
||
Зробив інтегрування по частинам, знайдемо:
∫ x ln xdx = |
x2 |
ln x − ∫ |
x2 |
|
dx |
= |
x2 |
ln x − ∫ |
x |
dx = |
x2 |
ln x − |
x2 |
+ C. |
|
|
x |
|
|
|
|
||||||||
2 |
2 |
|
2 |
2 |
2 |
4 |
|
|||||||
10
4) Для інтегралів виду: |
∫ Pn (x) arcsin xdx , |
|
∫ Pn (x) arccos xdx , |
||||||||||||||||||
∫ Pn (x)arctgxdx , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
∫ Pn (x)arcctgxdx , діємо |
аналогічно, |
як і в |
|||||||||||||||||||
випадку 3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приклад 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Знайти |
∫ xarctgxdx. . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Нехай |
u = arctgx , |
dv = dx , |
тоді du = |
|
dx |
, v = x . |
|||||||||||||||
|
+ x2 |
||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||
∫arctgxdx = x arctgx − ∫ |
x |
|
dx = xarctgx − |
1 |
ln |
|
1+ x2 |
|
|
+ C. |
|||||||||||
|
|
|
|||||||||||||||||||
1+ x |
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ЗАВДАННЯ 2.
Знайти об’єм продукції, випущеної за 5 років, якщо функція
Кобба - Дугласа має вид g(t) = (1 + 2t)e4t . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Розв’язок |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Об’єм продукції за T років складає: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
T |
|
|
|
5 |
|
|
|
|
|
|
|
u = 1 + 2t; du = 2dt |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Q = ∫ g (t)dt = ∫ (1 + 2t)e4t dt = |
|
dv = e |
4t |
dt; v = |
1 |
e |
4t |
|
= |
|||||||||||||||||||||
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1 + 2t e4t |
0 |
− 1 |
5 |
|
|
11 e |
20 − 1 − |
1 e 4 t |
0 = |
|
|
|
|
|||||||||||||||||
∫ e4t dt = |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
4 |
|
|
|
|
2 0 |
|
|
4 |
|
4 |
|
|
8 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= |
11 |
e 20 − |
1 |
− |
1 |
e 20 + |
1 |
= |
21 |
e20 − |
1 |
= |
1 |
(21e20 − 1). |
||||||||||||||||
4 |
|
|
4 |
|
8 |
|
8 |
|
8 |
|
8 |
|
|
8 |
|
|
|
|
|
|
|
|
||||||||
