Mathcad - КП Tраннсформатор тока
.pdfПовна вартість дроту ТС:
Cпр := Cпр1 + Cпр2
Cпр = 73607 гр.
Вага та вартість сталі:
Gст := γст×lм×Sм
= ´ 3
Gст 1.769 10кг. Cст := Цст×Gст
Cст = 1457563 гр.
Повна вартість активних матеріалів: Cам := Cпр + Cст
Cам = 1531171 гр.
2 РОЗРАХУНОК ЕЛЕКТРОДИНАМІЧНОЇ СТІЙКОСТІ ТРАНСФОРМАТОРА
Допустима напруга на викривлення в матеріалі обмоток: σдоп := 60 МПа. Коефіцієнт, що враховує взаємне розташування та розміри провідників:
æ 16×Rö
K'ф := lnè d1 ø - 0.5 K'ф = 1.7
Граничне значення струму електродинамічної стійкості ТС:
|
|
|
|
|
|
iдін := |
σдоп×q1р |
|
|
||
K'ф×10− 7 |
|||||
|
|
|
|
||
iдін = 179305 |
А. |
||||
У відповідності з вимогами ДЕСТ струм динамічної стійкості повинен бути більшим за струм термічної стійкості помножений на коефіцієнт 1.8×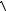
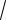2 :
iдін ³ 1.8×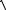
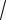2×n1t×I1н = 1
3 РОЗРАХУНОК ПОХИБОК ТРАНСФОРМАТОРА |
|
3.1 Параметри вторинного контура |
|
Повний опір навантаження: |
|
Zн := S2н |
|
I2н2 |
|
Zн = 15.75 Ом. |
i := 1 .. 5 |
При заданому навантаженні у вторинній обмотці наводиться ЕРС: |
|
æ 0.05 ö |
æ |
Zн |
||
ç |
0.2 |
÷ |
ç |
Zн |
ç |
÷ |
ç |
||
Ki1 := ç |
1 |
÷ |
Zн := ç |
Zн |
ç |
1.2 |
÷ |
ç |
0.25×Zн |
ç |
1 |
÷ |
ç |
0 |
è |
ø |
è |
||
öæ 0.0075 ö
÷ç 0.0035 ÷
÷ç ÷
÷ç 0.005 ÷
÷ç 0.002 ÷
÷ç ÷
ø è 0.002 øf :=
Активна та реактивна складові опора навантаження: |
|
|
|||||||||
Rн := Zн×0.8 |
|
|
|
|
|
|
|
|
|
|
|
RнT = ( 12.6 |
12.6 |
12.6 |
3.15 |
0 ) |
Ом. |
||||||
|
|
|
|
|
|
|
|
|
|
||
Xн := Zн×0.6 |
|
|
|
|
|
|
|
|
|
|
|
XнT = ( 9.45 |
9.45 |
9.45 |
2.362 |
0 ) |
Ом. |
||||||
|
|
|
|
|
|
|
|
|
|
||
Повний опір вторинного контура: |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
Z2i := |
(Rнi + r2)2 + (Xнi)2 |
|
|
|
|
||||||
Z2T = ( 16.185 16.185 16.185 4.381 0.539Ом) . |
|||||||||||
Кратність вторинного струму: |
|
|
|
|
|
|
|
|
|
|
|
Ki2i := Ki1i×(1 - fi) |
|
|
|
|
|
|
|
|
|
||
Ki2T = |
|
|
|
|
|
|
|
||||
0.05 |
0.199 |
|
0.995 |
1.198 |
0.998 |
|
|||||
ЕРС у вторинній обмотці: |
|
|
|
|
|
|
|
|
|
|
|
Eм2i := I2н×Ki2i×Z2i |
|
|
|
|
|
|
|
||||
Eм2T = ( 1.606 6.451 32.208 |
10.493 1.077 ) В. |
||||||||||
3.2 Параметри повного потоку розсіювання
Зовнішній діаметр магнітопроводу:
Dн := Dвн + 2×Tм×103
Dн = 892.507 |
мм. |
||||||
Dср := |
Dвн + Dн |
|
|||||
|
|
|
|
|
|||
|
2 |
|
|
|
|||
Dср = 593.872 |
мм. |
||||||
R2 |
:= |
Dср - d1 |
|
|
|||
|
|
|
|
||||
|
2 |
|
|
|
|||
R2 = 185.277 |
мм. |
||||||
R1 |
:= |
d1 |
|
||||
|
|
|
|
|
|||
2 |
|
|
|
|
|||
R1 = 111.659 |
мм. |
||||||
R0 |
:= |
R1 + R2 |
|
|
|||
|
|
||||||
|
2 |
|
|
|
|||
R0 = 148.468 |
мм. |
||||||
Питома провідність шляху потоку розсіювання ТС: Gσ' := 0.68 м.
Повна провідність шляху потоку розсіювання ТС з магнітопроводом квадратного перерізу можна одержати:
Gσкв := 2×π×Gσ'×R0×10− 3
Gσкв = 0.634 |
|
|
|
м. |
|
||
Тепер необхідно урахувати провідність в області розміром (hm-Tм): |
|||||||
Gσ := 2×Gσ'×(hm - Tм) |
|||||||
Провідність шляху потоку розсіювання ТС з магнітопроводом |
|||||||
прямокутного перерізу: |
|
|
|
|
|
|
Gσ |
Gσ := Gσкв + |
|
||||||
Gσ = 0.82 |
|
м. |
|||||
Амплітудне значення магнітного потоку розсіювання може бути знайдено за |
|||||||
наступною формулою: |
|
|
|
|
|
|
|
Фσм := 4×π× |
|
×10− 7×Gσ×I1н×W1 |
|||||
2 |
|||||||
Фσм |
= |
|
´ |
− 4 |
Вб. |
||
1.457 |
10 |
|
|||||
|
|
|
|
|
|||
3.3 Розподіл магнітної індукції по довжині магнітопровода
Густина потоку розсіювання в магнітопроводі ТС: |
|
||||||||||
4 |
|
π×10− 7 |
×Gσ×I1н×W1×Ki1i×W2слой |
|
|||||||
2 |
|
||||||||||
Bσдрi := |
|
|
|
|
|
|
|
|
|||
|
|
Sм×W2 |
|
|
|
|
|||||
BσдрT = |
|
|
|
|
|
|
|
|
|||
7.01·10-4 |
|
0 |
|
0.01 |
0.02 |
|
0.01 |
||||
Магнітна індукція від потоку взаємоіндукції запишеться:
|
|
Bм2i |
:= |
|
I2н×Ki2i×Z2i |
||||
|
|
|
222×Sм×W2 |
|
|||||
|
|
|
|
|
|
||||
Bм2T = |
|
|
|
|
|
|
|
||
0.00116 |
0.00466 |
|
|
0.02326 |
0.00758 |
0.00078 |
|||
Густина повного магнітного потоку в магнітопроводі:
Тл.
Тл.
Bсумi := 
(Bм2i)2 + (Bσдрi)2
BсумT = |
|
|
|
|
|
Тл. |
1.355·10-3 |
5.437·10-3 |
0.027 |
0.018 |
0.014 |
Значення магнітної індукції в будь-якому перерізі вільної частини магнітопровода:
q := 11 k := 1 .. q
|
|
æ |
|
|
æ |
|
k |
öö2 |
+ (Bм2i) |
2 |
|
Bk, i := |
èBσдрi×sin |
èπ× |
|
|
øø |
|
|||||
q + 1 |
|
||||||||||
|
0.0012 |
0.0047 |
|
0.0235 |
0.0087 |
0.0037 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
0.0012 |
0.0049 |
|
0.0243 |
0.0113 |
0.0071 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
0.0013 |
0.0051 |
|
0.0253 |
0.0141 |
0.0099 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
0.0013 |
0.0053 |
|
0.0262 |
0.0164 |
0.0122 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
B = |
0.0013 |
0.0054 |
|
0.0269 |
0.0179 |
0.0136 |
|
|
|||
|
|
|
|
|
|
|
|
||||
0.0014 |
0.0054 |
|
0.0272 |
0.0184 |
0.014 |
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
0.0013 |
0.0054 |
|
0.0269 |
0.0179 |
0.0136 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
0.0013 |
0.0053 |
|
0.0262 |
0.0164 |
0.0122 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
0.0013 |
0.0051 |
|
0.0253 |
0.0141 |
0.0099 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
0.0012 |
0.0049 |
|
0.0243 |
0.0113 |
0.0071 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
0.0012 |
0.0047 |
|
0.0235 |
0.0087 |
0.0037 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
3.4 Струм намагнічування з урахуванням нерівномірності розподілення магнітної індукції в магнітопроводі
Нерівномірність роподілення магнітної індукції по довжині магнітопровода можна оцінити за допомогою критерія:
Bсумi
ξi := Bм2i - 1
ξT = ( 0.17 0.17 0.17 1.43 17.05 )
При розрахунку приймається припущення, що магнітна індукція в будь-якому перерізі по довжині j-го елемента магнітопровода однакова, а величіна індукції визначається таким чином:
j := 1 .. 5
B'j , i := 0.5×(Bj ,i + Bj+1, i)
|
0.001 |
0.005 |
0.024 |
0.01 |
0.005 |
|
|
|
|
|
|
B' = |
0.001 |
0.005 |
0.025 |
0.013 |
0.008 |
|
|
|
|
|
|
0.001 |
0.005 |
0.026 |
0.015 |
0.011 |
|
|
|
|
|
|
|
|
0.001 |
0.005 |
0.027 |
0.017 |
0.013 |
|
|
|
|
|
|
|
0.001 |
0.005 |
0.027 |
0.018 |
0.014 |
|
|
|
|
|
|
Значення напруженності магнітного поля в сталі і-го елемента вільної частини магнітопроводу і кута втрат у сталі:
æ |
0.4 |
1.40 |
4.5 |
3.25 |
2.1 |
ö |
æ 17.4 |
19.25 |
29 |
24.8 |
21.1 |
ö |
|
ç |
0.4 |
1.40 |
4.5 |
3.35 |
2.2 |
÷ |
ç |
17.4 |
19.25 |
29 |
25.1 |
21.7 |
÷ |
ç |
÷ |
ç |
÷ |
||||||||||
H := ç |
0.4 |
1.40 |
4.5 |
3.45 |
2.336 |
÷ |
ψ := ç |
17.4 |
19.25 |
29 |
25.4 |
22.1 |
÷ |
ç |
0.168 |
0.615 |
2.3 |
1.737 |
1.2 |
÷ |
ç |
39.05 |
39.75 |
47 |
43.7 |
41.20 |
÷ |
ç |
0.168 |
0.615 |
2.3 |
1.768 |
1.232 |
÷ |
ç |
39.05 |
39.75 |
47 |
43.8 |
41.65 |
÷ |
è |
ø |
è |
ø |
||||||||||
Довжина часини магнітопровода під вторинною обмоткою: l2 := lм× 360α2
l2 = 0.617 м.
Довжина елемента свободної частини магнітопровода: lk := 0.1×(lм - l2)
lk = 0.125 м.
Складові напруженості магнітного поля в сталі магнітопровода:
|
|
|
æ π×ψj , iö |
|
|
|
æ π×ψj , iö |
|
|
||||||
|
Hxj ,i := Hj ,i×cosç |
|
|
|
÷ |
|
Hyj ,i := Hj ,i×sinç |
|
÷ |
|
|
||||
|
180 |
|
|
180 |
|
|
|||||||||
|
|
|
è |
ø |
|
|
|
è |
ø |
|
|
||||
æ |
0.38 |
1.32 |
3.94 |
2.95 |
1.96 |
ö |
æ 0.12 |
0.46 |
2.18 |
1.36 |
0.76 ö |
||||
ç |
0.38 |
1.32 |
3.94 |
3.03 |
2.04 |
÷ |
ç |
0.12 |
0.46 |
2.18 |
1.42 |
0.81 |
÷ |
||
ç |
÷ |
ç |
÷ |
||||||||||||
Hx = ç |
0.38 |
1.32 |
3.94 |
3.12 |
2.16 |
÷ |
Hy = ç |
0.12 |
0.46 |
2.18 |
1.48 |
0.88 |
÷ |
||
ç |
0.13 |
0.47 |
1.57 |
1.26 |
0.9 |
÷ |
ç |
0.11 |
0.39 |
1.68 |
1.2 |
0.79 |
÷ |
||
ç |
0.13 |
0.47 |
1.57 |
1.28 |
0.92 |
÷ |
ç |
0.11 |
0.39 |
1.68 |
1.22 |
0.82 |
÷ |
||
è |
ø |
è |
ø |
||||||||||||
Так само визначаються складові напруженості магнітного поля в сталі частини магнітопровода під вторинною обмоткою:
|
|
æ |
0.4 |
ö |
æ 17.4 ö |
||
|
|
ç |
|
÷ |
ç |
|
÷ |
|
0.001 |
1.4 |
19.25 |
||||
|
|
ç |
÷ |
ç |
÷ |
||
|
0.005 |
||||||
Bм2 = |
|
Hм2 := ç |
4.5 |
÷ |
ψм2 := ç |
28.4 |
÷ |
0.023 |
|||||||
|
|
ç |
|
÷ |
ç |
|
÷ |
|
0.008 |
1.551 |
43.1 |
||||
|
|
||||||
|
0.001 |
ç |
÷ |
ç |
÷ |
||
|
|
|
|||||
|
|
è |
0.888 |
ø |
è |
40.30 |
ø |
|
|
||||||
|
|
æ π×ψм2iö |
|
|
||||||
Hм2xi := |
Hм2i×cosç |
|
|
|
|
÷ |
|
|
||
180 |
|
|
|
|
||||||
|
|
è |
ø |
|
|
|||||
Hм2xT = |
|
|
|
|
|
|
|
|||
0.382 |
1.322 |
3.958 |
1.132 |
0.677 |
||||||
|
|
æ π×ψм2iö |
|
|
||||||
Hм2yi := |
Hм2i×sinç |
|
|
|
|
÷ |
|
|
||
|
180 |
|
|
|
||||||
|
|
è |
|
ø |
|
|
||||
Hм2yT = |
|
|
|
|
|
|
||||
0.12 |
0.462 |
|
2.14 |
1.06 |
0.574 |
|||||
Результуюча МРС визначається геометричним додаванням складових МРС по вісям обраної системи координат:
5
Fxi := 2×lk× å Hxk ,i + Hм2xi×l2 k = 1
FxT = ( 0.587 2.042 6.174 3.604 2.414 )
5
Fyi := 2×lk× å Hyk ,i + Hм2yi×l2 k = 1
FyT = ( 0.216 0.827 3.795 2.324 1.368 )
F0i := 
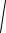(Fxi)2 + (Fyi)2
F0T = ( 0.625 2.203 7.248 4.289 2.774 )
Кут зсуву вектора результуючої МРС відносно вісі Х:
æ Fyiö
αi := atanç ÷
è Fxiø
αT = ( 0.353 0.385 0.551 0.573 0.516 )
Струм намагнічування визначається по значенню повної МРС:
I0i := F0i
W1
I0T = ( 0.625 2.203 7.248 4.289 2.774 )
3.5 Похибки трансформатора
Кут зсуву вектора МРС відносно вектора вторинного струму, обумовлений характером навантаження:
|
|
|
ϕ2i := |
æ |
Xнi |
ö |
|
|
|
|
|
|
|
atanç |
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
è Rнi + r2 |
ø |
|
|
|
||
|
|
|
ϕ2T = ( 0.624 0.624 0.624 0.57 0 ) |
|||||||
Струмова та кутова похибки ТС: |
|
|
|
|
|
|
||||
fi := |
I0i |
|
×sin(αi + ϕ2i)×100 |
|
δi := |
|
I0i |
×cos(αi |
+ ϕ2i)×3440 |
|
I1н×Ki1 |
|
|
I1н×Ki1 |
|
||||||
|
|
i |
|
|
|
i |
|
|
||
fT = ( 10.36 9.32 6.69 3.25 1.37 ) |
|
δT = ( 240.77 202.06 96.2 51.08 83.04 |
||||||||
3.6 Виткова корекція трансформатора
|
Число відмотаних вторинних витків: |
Wот := 1 |
|
|
fдi := |
|
|
Струмову похибку можна розрахувати наступним чином: |
|
1.5 |
|||
|
|
Wот |
|
|
|
0.75 |
|
|
fотi := -fi + W2 |
×100 |
|
|
0.6 |
|
|
fотT = ( -8.362 -7.318 -4.686 |
-1.251 |
0.632 ) |
0.6 |
|
|
|
|
||||
|
|
|
|
|
|
i := 1 .. 4 |
|
5 |
|
|
|
|
|
|
1.667 |
|
|
|
|
|
− fi |
− 1.667 0 |
0.5 |
|
1 |
|
|
fотi |
|
|
|
|||
|
|
|
|
|
|
|
fдi |
− 5 |
|
|
|
|
|
|
|
|
|
|
|
|
− fдi |
− 8.333 |
|
|
|
|
|
|
− 11.667 |
|
|
|
|
|
|
− 15 |
|
|
|
|
|
|
|
|
Ki1i |
|
|
|
Рисунок 3.1 - Залежність струмової похибки від кратності первинного струму |
||||||
250 |
|
|
|
210 |
|
|
|
170 |
|
|
|
δi |
|
|
|
130 |
|
|
|
90 |
|
|
|
50 |
0 |
0.5 |
1 |
|
|
|
Ki1i |
Рисунок 3.2 - Залежність кутової похибки від кратності первинного струму |
|||
3.7 Розрахунок максимальної кратності вторинного струму
Значення найбільшої кратності вторинного струму будемо розраховувати для трьох випадків.
Перший випадок: |
|
|
|
|
|
Bнас := 1.65 |
Тл. |
Ki1 := 1 |
Zн = Zном |
||
Bном1 := Bм23 |
|
|
|||
Bном1 = 0.0233 |
Тл. |
|
|||
Ki2max |
:= |
|
Bнас |
+ 5 |
|
|
|
|
|||
1 |
|
Bном1 |
|
|
|
|
|
|
|
||
Ki2max1 |
= 75.94 |
|
|
||
Другий випадок: Bнас := 1.65 |
Тл. |
Ki1 := 1.2 |
Zн = Zmin |
||
Bном2 := Bм24
Bном2 = 0.0076 Bнас
Bном2
Ki2max2 = 222.737
Тл.
+ 5
Третій випадок: |
Bнас := 1.65 |
|
Тл. |
Ki1 := 1 |
Zн := 0 |
|
|||||||||||
|
|
|
|
|
Bном3 := Bм25 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Bном = 7.776 × 10− 4 |
Тл. |
i := 1 |
.. 3 |
|||||||||
|
|
|
|
|
3 |
|
Bнас |
|
|
|
|
|
|||||
|
|
|
|
|
Ki2max := |
|
|
+ 5 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
3 |
Bном3 |
|
|
|
|
|||||||
|
|
|
|
|
Ki2max3 = 2.127 × 103 |
|
|
|
|
||||||||
Ki2дійснi := if (Ki2maxi < n1t ,Ki2maxi ,n1t) |
|
|
|
|
|||||||||||||
Rez := augment(Bном ,Ki2max ,Ki2дійсн) |
|
|
|
|
|||||||||||||
Таблиця 3.1 - Розрахунок максимальної кратності вторинного струму |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Внас |
Н(Внас) |
|
1.01x Внас |
Н(1.01x Внас) |
|
І1* |
|
Zн |
|
|
|||||||
Тл |
А/м |
|
Тл |
|
А/м |
|
|
|
|
% |
|
Ом |
|
|
|
||
1.65 |
410 |
|
1.666 |
|
600 |
|
|
|
100 |
|
Zном |
|
|
|
|||
|
|
|
|
|
120 |
|
Zmin |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
100 |
|
0 |
|
|
|
||
|
æ |
0.023 |
75.94 |
|
49 ö |
|
|
|
|
|
|
|
|
||||
|
ç |
7.578 × 10− 3 |
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
||
Rez = ç |
222.737 |
|
49 |
÷ |
|
|
|
|
|
|
|
|
|||||
|
ç |
7.776 |
× 10− 4 |
2.127 × 103 |
|
49 |
÷ |
|
|
|
|
|
|
|
|
||
|
è |
|
ø |
|
|
|
|
|
|
|
|
||||||