I2 i3

Рисунок 8 – К определению циркуляции вектора

В магнитном поле электрического тока величина этого интеграла зависит от того, охватывается ли проводник с током контуром интегрирования.

(22)

В общем случае, когда контур интегрирования охватывает несколько проводников произвольной формы, несущих токи , (рис. 8) то уравнение (22) имеет вид:

(23)

где - представляет алгебраическую сумму токов, охваченных контуром.

Полученное соотношение носит название теоремы о циркуляции напряженности магнитного поля или закон полного тока (закона Ампера).

Согласно этой теоремы циркуляция вектора напряженности магнитного поля по замкнутому контуру равна алгебраической сумме токов, пронизывающих поверхность, ограниченную контуром .

В теории магнитного поля соотношение (23) играет ту же роль, что и равенство 0-Г в теории электростатического поля.

,

и выражение (22) можно представить в виде:

. (24)

Выражение (24) представляет закон полного тока в интегральной форме (закон Ампера )

Ротор вектора

В электростатике переход к дифференциальной форме теоремы 0-Г потребовал введение дифференциальной операции над вектором - дивергенции вектора. Аналогично, для получения дифференциальной формы теоремы о циркуляции необходимо ввести новую дифференциальную операцию над вектором, носящую название ротора или вихря вектора.

Ротор вектора есть дифференциальная операция над вектором, образующая новый вектор.

Определим ротор вектора как предел отношения циркуляции векторапо контуру, к площади, ограниченной контуром, когда эта площадь стремиться к нулю. Записьозначает, что:

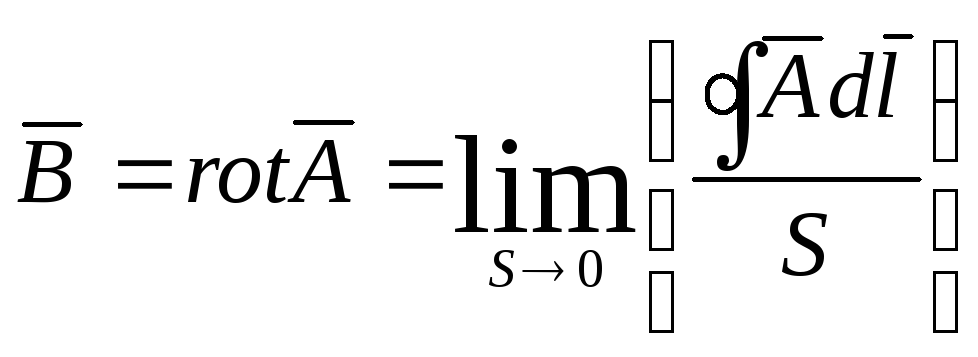. (25)

Теорема Стокса

Эта теорема связывает поверхностный интеграл с интегралом по замкнутому контуру.

(26)

Согласно этой теоремы циркуляция вектора по замкнутому контуру равна потоку его ротора через поверхность, ограниченную этим контуром.

Операцию можно записать в виде определителя

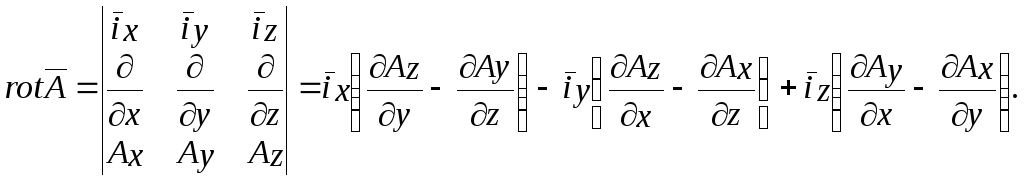
Закон полного тока в дифференциальной форме

Рассмотрим произвольный контур в магнитном поле постоянности тока. Согласно теорема о циркуляции вектора напряженности магнитного поля (23)

_,

где: - алгебраическая сумма токов, текущих внутри контура.

Если контур стягивает некоторую поверхность, то все эти токи протекают через поверхность. Поэтомуможно представить как

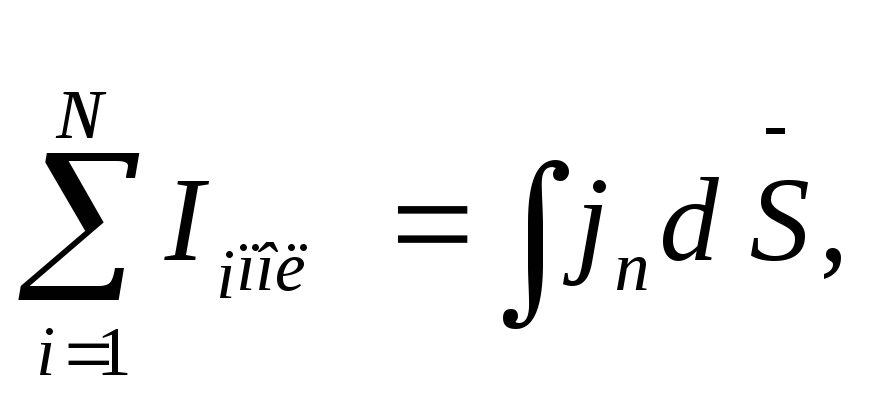
где jn – плотность тока.

Тогда уравнение (23) будет иметь вид:

(27)

Левую часть уравнения (27) по теореме Стокса (26) можно преобразовать

тогда выражение (27) будет иметь вид:

.

Так как это равенство выполняется для произвольной поверхности , то из него вытекает равенство подынтегральных выражений

, (28)

где -добавил Максвелл.

Это уравнение связывает плотность тока с напряженностью магнитного поля и представляет собой закон полного тока в дифференциальной форме.

Полная система дифференциальных уравнений, определяющих магнитное поле, будет иметь вид:

, . (29)

Закон электромагнитной индукции

В 1831 г. Майкл Фарадей установил, что если через поверхность , ограниченную проводящим контуром, проходит меняющийся во времени магнитный поток, то в контуре возникает электродвижущая сила (ЭДС) индукции.

. (30)

Эту ЭДС можно рассматривать как циркуляцию вектора напряженности электрического поля по контуру проводника, так что

, т. к. то

Меняя порядок дифференцирования и интегрирования, получим:

. (31)

Таким образом, явление электромагнитной индукции заключается в том, что при изменении со временем магнитного поля, пронизывающего поверхность, ограниченную проводящим контуром, в проводнике возникает электрическое поле, циркуляция напряженности которого по контуру проводника (ЭДС) равна взятой со знаком "-"скорости изменения магнитного потока во времени. Уравнение (31) выражает закон электромагнитной индукции в интегральной форме.

Представим уравнение (31), выражающее связь между электрическим и магнитным полем в любой среде, в дифференциальной форме. Применим к левой части уравнения (31) теорему Стокса (26) получим

, или

. (32)

Полученное уравнение выражает закон электромагнитной индукции в дифференциальной форме. Из выражения (32) следует, что изменение магнитного поля во времени приводит к изменению электрического поля в пространстве.