Преобразование интеграла по поверхности в интеграл по объему

Пользуясь понятием дивергенции, получим важное интегральное соотношение, известное в математике под преобразованием 0-Г.

Рассмотрим объем , ограниченный поверхностью.

Разобьем этот объем на бесконечное число бесконечно малых параллелепипедов. Для каждого параллелепипеда в соответствии с определением дивергенции запишем

,

где - б/м поток через грани одного из параллелепипедов. Составляя подобные выражения для всех параллелепипедов, на которые разбит объем и суммируя, получим:

, или

(9)

Электрический ток. Плотность тока

Введем понятие о электрическом токе. Электрическим током через замкнутую поверхность назовем скорость изменения зарядав объеме, ограниченном поверхностью

(10)

"-" говорит о том, что заряд в рассматриваемом объёме уменьшается.

Распределение электрического тока по поверхности характеризуется вектором плотности тока. Он направлен в сторону движения положительных зарядов и численно равен:

(11)

где - вектор-площадка; откуда

(12)

Подставим (12) в (10), получим:

(13)

Уравнение (13) представляет закон сохранения заряда в интегральной форме, поскольку оно связывает поток вектора плотности электрического тока через замкнутую поверхность с изменением заряда во всем объеме.

Получим дифференциальное выражение этого закона. Для этого представим общий заряд в объемев виде:

(14)

где – объёмная плотность заряда.

Выражение (13) запишем с учетом (14) в виде:

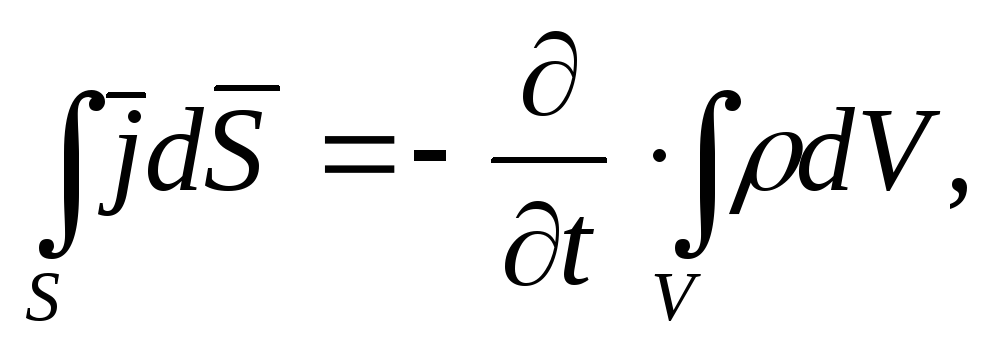
или меняя порядок интегрирования и дифференцирования

(15)

Преобразуя поверхностный интеграл левой части на основании теоремы 0-Г (9) в интеграл по объему

получим

Приравнивая подынтегральные выражения получим закон сохранения заряда в дифференциальной форме или уравнение непрерывности

(16)

Согласно уравнению (16) истоками тока являются те точки пространства, где плотность заряда изменяется со временем.

Ток смещения

Как известно, объемная плотность заряда связана с вектором электрической индукции соотношением

.

Подставляя это соотношение в уравнение (16) имеем

;

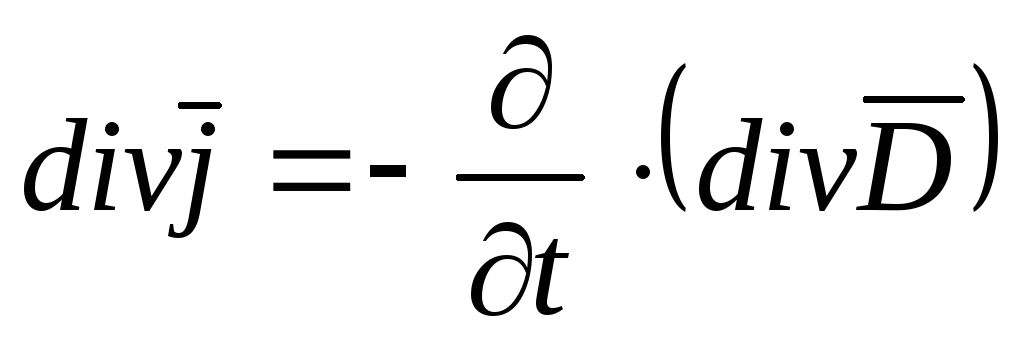Меняем местами порядок дифференцирования по времени и по пространственным координатам, получим:

или (17)

Полученное выражение показывает, что вектор, представляющий собой сумму вектора и вектора , непрерывен, т.е. вектор дополняет вектор плотности тока до замкнутости.

Максвелл ввел понятие о плотности тока смещения , понимая под ним изменение электрического поля во времени

(18)

, где , то

.

Полученное выражение представляет собой уравнение непрерывности в дифференциальной форме.

Для понимания физического смысла тока смещения рассмотрим цепь, состоящую из и(рис. 3)

А

В

I_см

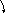
Рисунок 3 – К определению тока смещения

При заряде или разряде конденсатора в соединительном проводнике существует ток проводимости. Этот ток терпит разрыв у пластин конденсатора, т.к. среда между пластинами является диэлектриком. Однако суммарный ток проводимости и смещения непрерывен во всей цепи. В обкладку из соединительного провода вытекает ток, состоящий из тока проводимости и тока смещения. Из обкладкивытекает в диэлектрик ток смещения. Этот ток смещения равен:

,

где - площадь пластин;

подставляем выражение для тока смещения получим:

,

где - напряжение на обкладках конденсатора;

- расстояние между ними;

или

Полученное соотношение представляет собой хорошо известное выражение для емкостного тока конденсатора, который равен протекающему к обкладкам конденсатора току проводимости.

Введение понятия о токе смещения позволило Максвеллу сделать обобщения, в результате которых Генриху Герцу удалось теоретически предсказать и экспериментально обнаружить существование электромагнитных волн, а великому русскому ученому А.С. Попову положить начало новой отрасли техники - радиотехники. Введение тока смещения имело большое значение для электродинамики, поскольку при этом устанавливалась внутренняя взаимосвязь электрического и магнитного полей. Действительно, изменение во времени электрического поля в какой-либо точке пространства приводит к протеканию тока смещения, который, в свою очередь, вызывает появление магнитного поля

Максвелл предложил ввести ток смещения в правую часть закона полного тока