
4. Числовые характеристики выборки.
В качестве одной из важнейших характеристик вариационного ряда применяют среднюю величину. Математическая статистика различает несколько типов средних величин: арифметическую, геометрическую, гармоническую, квадратическую, кубическую и др. Все перечисленные типы средних могут быть исчислены для случаев, когда каждый из вариантов вариационного ряда встречается только один раз, - тогда средняя называется простой или невзвешенной, - и для случаев, когда варианты или интервалы повторяются различное число раз. При этом число повторений вариантов или интервалов называют частотой или статистическим весом, а среднюю, вычисленную с учетом статистического веса, - взвешенной средней.
Выбор одного из перечисленных типов средних для характеристики вариационного ряда производится не произвольно, а в зависимости от особенностей изучаемого явления и цели, для которой среднее исчисляется.
Практически при выборе того или иного типа средней следует исходить из принципа осмысленности результата при суммировании или при взвешивании. Только тогда средняя применена правильно, когда в результате взвешивания или суммирования получаются величины, имеющие реальный смысл.
Обычно затруднения при выборе типа средней возникают лишь в использовании средней арифметической или гармонической. Что же касается геометрической и квадратической средних, то их применение ограничено особыми случаями (см. далее).
Следует иметь в виду, что средняя только в том случае является обобщающей характеристикой, если она применяется к однородной совокупности. В случае использования средней для неоднородных совокупностей можно прийти к неверным выводам. Научной основой статистического анализа является метод статистических группировок, т. е. расчленения совокупности на качественно однородные группы.
Все указанные
типы средних величин могут быть получены
из формул степенной средней. Если имеются
варианты
![]() ,
,
![]() ,
... ,
,
... ,
![]() ,
то средняя из вариантов может быть
исчислена по формуле простой невзвешенной
степенной средней порядка
,
то средняя из вариантов может быть
исчислена по формуле простой невзвешенной
степенной средней порядка
![]()
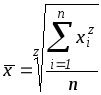 .
.
При наличии
соответствующих частот
![]() средняя исчисляется по формуле взвешенной
степенной средней
средняя исчисляется по формуле взвешенной
степенной средней
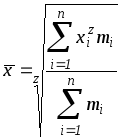 .
.
Здесь
![]() - степенная средняя,
- степенная средняя,
![]() - показатель степени, определяющий тип
средней,
- показатель степени, определяющий тип
средней,
![]() - варианты,
- варианты,
![]() - частоты или статистические веса
вариантов.
- частоты или статистические веса
вариантов.
Средняя
арифметическая
получается из формулы степенной средней
при подстановке
![]() :
:
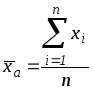
- средняя арифметическая невзвешенная и
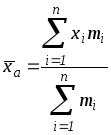
- средняя арифметическая взвешенная.
Средняя
гармоническая
получается при подстановке в формулу
степенной средней значения
![]() .
Средняя гармоническая простая
.
Средняя гармоническая простая
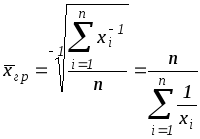 .
.
Средняя гармоническая взвешенная
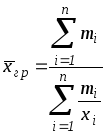 .
.
Средняя гармоническая
вычисляется в тех случаях, когда средняя
предназначается для расчета сумм
слагаемых, обратно пропорциональных
величине данного признака, т. е. когда
суммированию подлежат не сами варианты,
а обратные им величины
![]() ,
,
![]() ,
... ,
,
... ,
![]() .
.
Средняя
квадратическая
получается из формулы степенной средней
при подстановке
![]() .
.
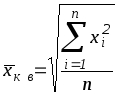
- средняя квадратическая невзвешенная и

- средняя квадратическая взвешенная. Средняя квадратическая используется только в тех случаях, когда варианты представляют собой отклонения фактических величин от их средней арифметической или от заданной нормы.
Средняя
геометрическая
получается из формулы степенной средней
при предельном переходе
![]() :
:
![]()
- средняя геометрическая невзвешенная и
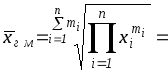
![]()
- средняя геометрическая взвешенная. Вычисления средней геометрической в значительной мере упрощаются применением логарифмирования. Для невзвешенной средней геометрической получаем:
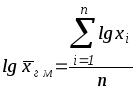 .
.
Для взвешенной средней геометрической получаем:
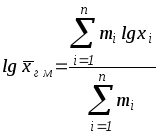 .
.
Таким образом, логарифм средней геометрической есть средняя арифметическая из логарифмов вариантов. Средняя геометрическая используется главным образом при изучении динамики. Расчет средних коэффициентов и темпов роста производится по формулам средней геометрической.
Если вычислить
различные типы средних для одного и
того же вариационного ряда, то численные
их значения будут отличаться друг от
друга. При этом средние по своей величине
расположатся в определенном порядке.
Наименьшей из перечисленных средних
окажется средняя гармоническая, затем
геометрическая и т. д., наибольшей -
средняя квадратическая. Порядок
возрастания средних при этом определяется
показателем степени
![]() в формуле степенной средней. Так,
в формуле степенной средней. Так,
при
![]() получаем среднюю гармоническую,
получаем среднюю гармоническую,
при
![]() - геометрическую,
- геометрическую,
при
![]() - арифметическую,
- арифметическую,
при
![]() - квадратическую:
- квадратическую:
![]()
![]()
![]()
![]() .
.
В качестве
характеристики вариационного ряда
применяется медиана
(![]() ),
т. е. такое значение варьирующего
признака, которое приходится на середину
упорядоченного вариационного ряда.
Если в вариационном ряде
),
т. е. такое значение варьирующего
признака, которое приходится на середину
упорядоченного вариационного ряда.
Если в вариационном ряде
![]() случаев, то значение признака у случая
случаев, то значение признака у случая
![]() будет медианным. Если в ряду четное
число
будет медианным. Если в ряду четное
число
![]() случаев, то медиана равна средней
арифметической из двух срединных
значений. Формулы для исчисления медианы
при нечетном и четном числе вариантов
случаев, то медиана равна средней
арифметической из двух срединных
значений. Формулы для исчисления медианы
при нечетном и четном числе вариантов
![]() ;
; ![]() .
.
При исчислении медианы интервального вариационного ряда сначала находят интервал, содержащий медиану, путем использования накопленных частот или частостей. Медианному интервалу соответствует первая из накопленных частот или частостей, превышающая половину всего объема совокупности. Для нахождения медианы при постоянстве плотности внутри интервала, содержащего медиану, используют следующую формулу:
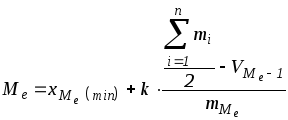 ,
,
где
![]() - нижняя граница медианного интервала,
- нижняя граница медианного интервала,
![]() - интервальная разность,
- интервальная разность,
![]() - накопленная частота интервала,
предшествующего медианному,
- накопленная частота интервала,
предшествующего медианному,
![]() - частота медианного интервала.
- частота медианного интервала.
Медиана может быть определена и графически по кумуляте. Для определения медианы по кумуляте последнюю ординату, пропорциональную сумме всех частот или частостей, делят пополам. Из полученной точки восстанавливают перпендикуляр до пересечения с кумулятой. Абсцисса точки пересечения и дает значение медианы (см. рис. 29).
Медиана обладает тем свойством, что сумма абсолютных величин отклонений вариантов от медианы меньше, чем от любой другой величины (в том числе и от средней арифметической):
![]() .
.
Это свойство медианы может быть использовани при проектировке расположения трамвайных и троллейбусных остановок, бензоколонок, ссыпных пунктов и т. д.
Пример 4.
На шоссе длиной
![]() км
имеется
км
имеется
![]() гаражей. Для проектирования строительства
бензоколонки были собраны данные о
числе предполагаемых ездок на заправку
с каждого гаража. Результаты обследования
представлены в следующей таблице:
гаражей. Для проектирования строительства
бензоколонки были собраны данные о
числе предполагаемых ездок на заправку
с каждого гаража. Результаты обследования
представлены в следующей таблице:
|
На каком километре шоссе расположен гараж |
7 |
26 |
28 |
37 |
40 |
46 |
60 |
78 |
86 |
92 |
Всего ездок |
|
Проектиру-емое число ездок |
10 |
15 |
5 |
20 |
5 |
25 |
15 |
30 |
10 |
65 |
200 |
Нужно поставить бензоколонку так, чтобы общий пробег машин на заправку был наименьший.
Р е ш е н и е. Вариант
1. Если
бензоколонку поставить на середине
шоссе, т. е. на
![]() -м
километре (средняя арифметическая), то
пробеги с учетом числа ездок составят:
-м
километре (средняя арифметическая), то
пробеги с учетом числа ездок составят:
а) в одном направлении
![]()
![]() км;
км;
б) в противоположном
направлении
![]()
![]() км.
км.
Общий пробег в
оба направления окажется равным
![]() км.
км.
Вариант
2. Уменьшения
пробега можно достигнуть, если бензоколонку
поставить на
![]() -м
километре, т.е. на среднем участке шоссе
с учетом числа ездок (средняя арифметическая
взвешенная). В этом случае пробеги
составят по
-м
километре, т.е. на среднем участке шоссе
с учетом числа ездок (средняя арифметическая
взвешенная). В этом случае пробеги
составят по
![]() км
в оба направления, т.е. общий пробег
составит
км
в оба направления, т.е. общий пробег
составит
![]() км
и окажется меньше, чем при первом
варианте, на
км
и окажется меньше, чем при первом
варианте, на
![]() км.
км.
Вариант
3. Наилучший
результат, т.е. минимальный общий пробег,
будет получен в том случае, если мы
поставим бензоколонку на
![]() -м
километре, что будет соответствовать
медиане. Тогда пробеги составят
-м
километре, что будет соответствовать
медиане. Тогда пробеги составят
![]() км
и
км
и
![]() км.
общий пробег равен
км.
общий пробег равен
![]() км,
т.е. он оказался меньше общих пробегов,
расчитанных по предыдущим вариантам.
км,
т.е. он оказался меньше общих пробегов,
расчитанных по предыдущим вариантам.
Модой
(![]() )
назыыается вариант, наиболее часто
встречающийся в данном вариационном
ряду. Для дискретного ряда мода, являющаяся
характеристикой вариационного ряда,
определяется по частотам вариантов и
соответствует варианту с наибольшей
частотой. В случае интервального
распределения с равными интервалами
модальный интервал (т. е. содержащий
моду) определяется по наибольшей частоте,
а при неравных интервалах - по наибольшей
плотности. Вычисление моды производится
по следующей формуле
)
назыыается вариант, наиболее часто
встречающийся в данном вариационном
ряду. Для дискретного ряда мода, являющаяся
характеристикой вариационного ряда,
определяется по частотам вариантов и
соответствует варианту с наибольшей
частотой. В случае интервального
распределения с равными интервалами
модальный интервал (т. е. содержащий
моду) определяется по наибольшей частоте,
а при неравных интервалах - по наибольшей
плотности. Вычисление моды производится
по следующей формуле
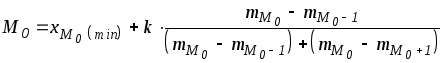 ,
,
где
![]() - нижняя граница модального интервала,
- нижняя граница модального интервала,
![]() - интервальная разность,
- интервальная разность,
![]() - частота модального интервала,
- частота модального интервала,
![]() - частота интервала, предшествующего
модальному,
- частота интервала, предшествующего
модальному,
![]() - частота интервала, последующего за
модальным.
- частота интервала, последующего за
модальным.
Вариационные ряды, в которых частоты вариантов, равноотстоящих от средней, равны между собой, называются симметричными. Особенностью симметричных вариационных рядов является равенство трех характеристик - средней арифметической, моды и медианы:
![]()
(это необходимое уусловие симметричности вариационного ряда, но не достаточное).
Вариационные ряды, в которых расположение вариантов вокруг средней неодинаково, т. е. частоты по обе стороны от средней изменяются по-разному, называются асимметричными, или скошенными. Различают левостороннюю и правостороннюю асимметрию.
Средние величины, характеризуя вариационный ряд одним числом, не учитывают вариацию признака, между тем эта вариация существует. Для измерения вариации признака математическая статистика применяет ряд способов.
Вариационный
размах (![]() ),
или широта распределения, есть разность
между экстремальными (крайними) значениями
вариационного ряда:
),
или широта распределения, есть разность
между экстремальными (крайними) значениями
вариационного ряда:
![]() ,
,
где
![]() - наибольший вариант вариационного
ряда,
- наибольший вариант вариационного
ряда,
![]() - наименьший вариант вариационного
ряда. Вариационный размах представляет
собой величину неустойчивую, чрезвычайно
зависящую от случайных обстоятельств;
применяется в качестве приблизительной
оценки вариации.
- наименьший вариант вариационного
ряда. Вариационный размах представляет
собой величину неустойчивую, чрезвычайно
зависящую от случайных обстоятельств;
применяется в качестве приблизительной
оценки вариации.
Среднее линейное
отклонение,
или
простое среднее отклонение (обозначается
буквой
![]() )
представляет собой среднюю арифметическую
из абсолютных значений отклонений
вариантов от средней. В зависимости от
отсутствия или наличия частот вычисляют
среднее линейное отклонение невзвешенное
или взвешенное:
)
представляет собой среднюю арифметическую
из абсолютных значений отклонений
вариантов от средней. В зависимости от
отсутствия или наличия частот вычисляют
среднее линейное отклонение невзвешенное
или взвешенное:
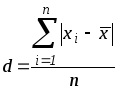 ;
; 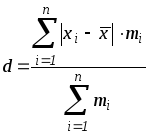 .
.
Средний квадрат
отклонения,
или дисперсия
(обозначается
![]() )
наиболее часто применяется в качестве
меры колеблемости признака. Дисперсию
невзвешенную и взвешенную вычисляют
по следующим формулам:
)
наиболее часто применяется в качестве
меры колеблемости признака. Дисперсию
невзвешенную и взвешенную вычисляют
по следующим формулам:
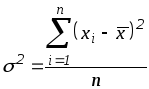 ;
; 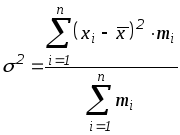 .
.
Таким образом, дисперия есть средняя арифметическая из квадратов отклонений вариантов от их средней арифметической.
Квадратный корень
из дисперсии
![]() называется среднеквадратическим
отклонением.
называется среднеквадратическим
отклонением.
Обобщающими характеристиками вариационных рядов являются моменты распределения. Характер распределения может быть определен с помощью небольшого числа моментов.
Средняя из
![]() -х
степеней отклонений вариантов
-х
степеней отклонений вариантов
![]() от некоторой постоянной величины
от некоторой постоянной величины
![]() называется моментом
называется моментом
![]() -го
порядка:
-го
порядка:
![]() .
.
При исчислении
средних в качестве весов могут быть
использованы частоты, частости или
вероятности. При использовании в качестве
весов частот или частостей моменты
называются эмпирическими, а при
использовании вероятностей - теоретическими.
Порядок момента определяется величиной
![]() .
Эмпирический момент
.
Эмпирический момент
![]() -го
порядка находится как отношение суммы
произведений
-го
порядка находится как отношение суммы
произведений
![]() -х
степеней отклонений вариантов от
постоянной величины
-х
степеней отклонений вариантов от
постоянной величины
![]() на частоты к сумме частот:
на частоты к сумме частот:
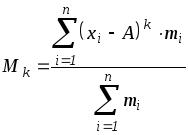 .
.
В зависимости от
выбора постоянной величины
![]() различают следующие моменты.
различают следующие моменты.
1) Если
![]() ,
то моменты называются начальными
и обозначаются
,
то моменты называются начальными
и обозначаются
![]() :
:
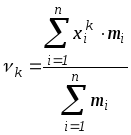 .
.
Тогда при
![]() получаем начальный момент нулевого
порядка
получаем начальный момент нулевого
порядка
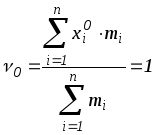 ;
;
при
![]() получаем начальный момент первого
порядка
получаем начальный момент первого
порядка
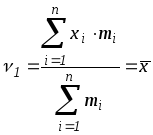 ;
;
при
![]() получаем начальный момент второго
порядка
получаем начальный момент второго
порядка
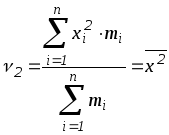 ;
;
при
![]() получаем начальный момент третьего
порядка
получаем начальный момент третьего
порядка
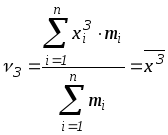 ;
;
при
![]() получаем начальный момент четвертого
порядка
получаем начальный момент четвертого
порядка
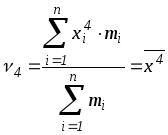 ,
,
и т.д. Практически используют моменты первых четырех порядков.
2) Если
![]() не равно нулю, а некоторой произвольной
величине
не равно нулю, а некоторой произвольной
величине
![]() (начало отсчета), то моменты называются
начальными относительно
(начало отсчета), то моменты называются
начальными относительно
![]() и обозначаются
и обозначаются
![]() :
:
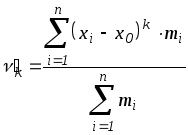 .
.
3) Если за постоянную
величину
![]() взять среднюю
взять среднюю
![]() ,
то моменты называются центральными и
обозначаются
,
то моменты называются центральными и
обозначаются
![]() :
:
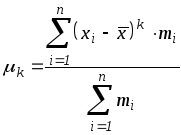 .
.
Тогда при
![]()
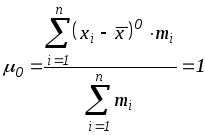
(центральный момент
нулевого порядка равен единице); при
![]()
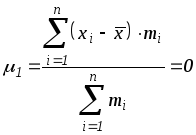
(центральный момент
первого порядка равен нулю); при
![]()
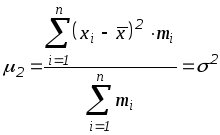
(центральный момент
второго порядка равен дисперсии и служит
мерой колеблемости признака); при
![]()
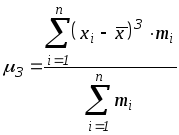
(центральный момент
третьего порядка служит мерой асимметрии
распределения признака. Если распределение
симметрично, то
![]() );
при
);
при
![]()
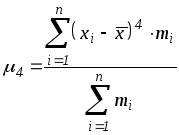
(центральный момент четвертого порядка).
Коэффициентом
асимметрии
![]() называется отношение центрального
момента третьего порядка к кубу
среднеквадратического отклонения:
называется отношение центрального
момента третьего порядка к кубу
среднеквадратического отклонения:
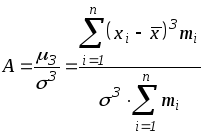
Если полигон вариационного ряда скошен, т. е. одна из его ветвей, начиная от вершины, зримо короче другой, то такой ряд называют асимметричным.
Эксцессом
называется уменьшенное на
![]() единицы отношение центрального момента
четвертого порядка к четвертой степени
среднеквадратического отклонения:
единицы отношение центрального момента
четвертого порядка к четвертой степени
среднеквадратического отклонения:
![]() .
.
Кривые распределения,
у которых
![]() ,
менее крутые, имеют более плоскую вершину
и называются плосковершинными.
Кривые распределения, у которых
,
менее крутые, имеют более плоскую вершину
и называются плосковершинными.
Кривые распределения, у которых
![]() ,
более крутые, имеют более острую вершину
и называются островершинными.
,
более крутые, имеют более острую вершину
и называются островершинными.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Чем занимается математическая статистика ?
2. Назовите основные задачи математической статистики.
3. Назовите основные понятия математической статистики.
4. Что такое гистограмма ? Полигон ? Кумулята ?
5. Какая разница между генеральной и выборочной совокупностью ?
6. Назовите числовые характеристики статистического распределения. Дайте определение этих характеристик.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Построить полигон по следующему вариационному ряду:
|
|
1 |
3 |
4 |
8 |
|
|
20 |
10 |
14 |
6 |
Найти ряд накопленных частостей и построить кумулятивную кривую.
2. Построить гистограмму и полигон по следующему вариационному ряду:
|
Интервалы |
0-1,5 |
1,5-3 |
3-4,5 |
4,5-6 |
|
Частости |
0,3 |
0,2 |
0,4 |
? |
Найти ряд накопленных частостей и построить кумулятивную кривую.
3. Вычислить моду, медиану и найти среднюю арифметическую, дисперсию, коэффициент асимметрии и эксцесс для следующего вариационного ряда:
|
|
12 |
14 |
16 |
18 |
20 |
22 |
|
|
0,05 |
0,15 |
0,5 |
0,16 |
0,1 |
0,04 |
Ответ:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
4. Найти среднюю арифметическую и среднее квадратическое отклонение для ряда распределения:
|
Интер- валы |
6,67- 6,69 |
6,69- 6,71 |
6,71- 6,73 |
6,73- 6,75 |
6,75- 6,77 |
6,77- 6,79 |
6,79- 6,81 |
6,81- 6,83 |
|
Часто- ты |
5 |
17 |
24 |
54 |
52 |
23 |
18 |
7 |
Ответ:
![]() ,
,
![]() .
.
