
- •Міністерство освіти та науки України
- •1 Хвилі в напрямних системах
- •1.1 Класифікація напрямлених хвиль
- •1.2 Поперечне хвильове число
- •1.3 Зв'язок між Es, Hs тa Ez, Hz
- •1.4. Загальні властивості напрямлених хвиль
- •2.1 Хвилі типу е в прямокутному хвилеводі
- •2.2 Круглий хвилевід
- •3 Коаксіальна лінія
- •Перелік посилань
3 Коаксіальна лінія
Це
двозв'язана напрямна система (може
протікати сталий струм). В напрямних
системах такого типу можливе існування
хвиль ТЕМ, Е та Н. Оскільки у хвилі ТЕМ
![]() (
(![]() ),
то ця хвиля є найнижчою, а тому основною.
Розглянемо окремо всі хвилі в коаксіальній
лінії.
),
то ця хвиля є найнижчою, а тому основною.
Розглянемо окремо всі хвилі в коаксіальній
лінії.

Рисунок 3.1 - Коаксіальна лінія
Хвиля ТЕМ в коаксіальній лінії
Оскільки
Ez=Hz=0,
то ![]() та
та ![]() задовільняють рівнянню
задовільняють рівнянню
![]() ;
;
![]() .
(24)
.
(24)
Із
рівності нулю повздовжних і нерівності
нулю поперечних складової поля
виходить, що ![]() ,
тому для хвилі ТЕМ
,
тому для хвилі ТЕМ
![]()
і стала поширення виражається чисто дійсним числом
![]() ,
де
,
де ![]() -
фазова швидкість хвилі ТЕМ, співпадаюча
зі швидкістю світла у діелектричному
середовищі, яке заповнює кабель.
-
фазова швидкість хвилі ТЕМ, співпадаюча
зі швидкістю світла у діелектричному
середовищі, яке заповнює кабель.
Величина
![]() від
від
![]() не
залежить, тобто дисперсія відсутня.
не
залежить, тобто дисперсія відсутня.
Нагадаємо, що (24) - це рівняння Лапласа. В свою чергу
![]() ,
(26)
,
(26)
де
![]() - скалярний потенціал, який теж задовольняє
рівнянню Лапласа
- скалярний потенціал, який теж задовольняє
рівнянню Лапласа
![]() .
(26)
.
(26)
Розв'яжемо його.
В
циліндричній системі координат оператор
![]()
![]()
Розв'яжемо це рівняння методом розділення змінних.
![]()
Підставимо в рівняння і отримаємо
![]() (а),
(а),
![]() (б)
(б)
тут m - ціле число, m=0,1,2... .
Вирішення рівняння (а) запишемо у формі
![]() ,
або
,
або
![]() .
Візьмемо
.
Візьмемо
![]() .
.
Вирішення рівняння (б) має вигляд
![]() ,
(в)
,
(в)
Тоді
повне вирішення при ![]() має вигляд
має вигляд
![]() .
.
Як неважко перевірити, це вирішення не задовільняє граничним умовам при r = R1 та r = R2 на поверхні провідника
![]()
і по цій причині його треба відкинути.
Візьмемо форму вирішення при m=0. Тоді
![]() ,
тоді
,
тоді ![]()
![]() ;
;
![]() ;
;
![]()
![]() ,
бо
,
бо ![]() від
від ![]() не залежить, тому
не залежить, тому ![]() (дорівнює тотожньо)
(дорівнює тотожньо)
при будь-яких значеннях констант С та D.
Набір
констант ![]() ,
,
![]() характерний
для сталого потенціалу, але ми розглядаємо
хвильовий процес, тому візьмемо
характерний
для сталого потенціалу, але ми розглядаємо
хвильовий процес, тому візьмемо ![]() ;
;
![]() .
Таким
чином маємо
.
Таким
чином маємо
![]() .
.
![]() ,
візьмемо похідні і отримаємо
,
візьмемо похідні і отримаємо
![]() ,
а звідси
,
а звідси ![]()
Константу D знайдемо через напруженність поля біля поверхні
внутрішнього провідника. Позначимо її Е0.
![]() ,
або
,
або ![]() .
Тоді
.
Тоді
![]() ,
,
![]()
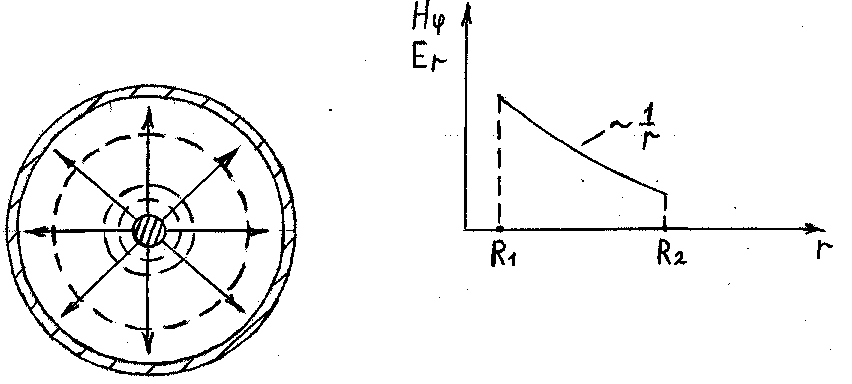
Рисунок 3.2 - Структура поля хвилі ТЕМ в КК
Потенціальний
характер ![]() дозволяє
говорити про різницю потенціалів між
провідниками коаксіалу.
дозволяє
говорити про різницю потенціалів між
провідниками коаксіалу.
![]() ,
а
звідси
,
а
звідси  .
.
![]() .
(90)
.
(90)
Струм, який протікає по поверхні центрального провідника та внутрішній поверхні наріжного провідника дорівнює
![]() .
(91)
.
(91)
Подробиці:
![]() ,
,
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]() .
.
Відношення
![]() в режимі біжучої хвилі зветься хвильовим
опором коаксіальної лінії.
в режимі біжучої хвилі зветься хвильовим
опором коаксіальної лінії.
 .
(92)
.
(92)
Особливості конструкції коаксіального кабеля (КК)
Коаксіальні кабелі використовуються на частотах до 3 ГГц. Конструкції залежать від призначення та діапазону частот.
Внутрішній провідник - мідний провід, який для зменшення втрат покривають сріблом. Для гнучких конструкцій використовують провід скручений з 7, 19, 37 проводів.
Зовнішній провідник - мідна стрічка, або сітка. Інколи покривають сріблом.
Вітчизняна промисловість масово випускає кабелі з zx=15 Ом та zx=50 Ом. Вибір таких значень zx зв'язаний з компромісом між втратами, допустимою напругою та максимальною потужністю. Кабелі з zx=75 Ом звичайно оп-тимізовані по втратам, з zx=50 Ом - це компроміс між всіма оптимумами.
Ізоляція - поліетилен, гума, або навивається із фторопластової стрічки. Інколи виготовляються кабелі з шайбовою ізоляцією - це, як правило, негнучкі кабелі, які використовують в магістральних лініях зв'язку на далекі відстані.
Хвилі вищого типу в коаксіальній лінії
Хвилі типу Е - електричні хвилі
Умова:
![]() ,
,
![]() .
.
Запишемо рівняння Гельмгольца відносно Ez в циліндричній системі координат - вираз (50)
![]() .
(93)
.
(93)
Розв'язуючи це рівняння методом розділення змінних отримаємо
![]() .
(94)
.
(94)
Оскільки
точка г=0 знаходиться зовні тої області,
де є е. м. п. хвилі, то в вирішенні (62) нема
потреби відкидати функцію Неймана Nm,
яку
не враховують в задачі для круглого
хвилеводу. Використаємо граничну умову
![]() і отримаємо
і отримаємо
 .
(95)
.
(95)
Ця
система однорідних лінійних алгебраїчних
рівнянь має нетривіальне вирішення
(тобто ![]() ,
,
![]() )
в тому випадку, коли визначник її дорівнює
нулю, (det=0),
тобто
)
в тому випадку, коли визначник її дорівнює
нулю, (det=0),
тобто
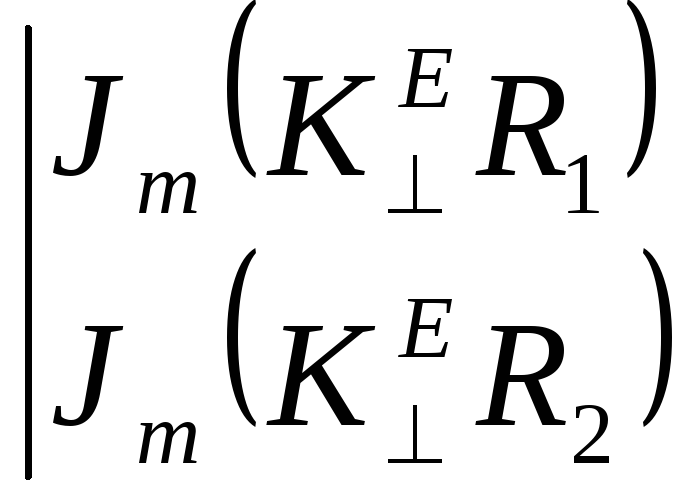
 .
(96)
.
(96)
Знайшовши визначник по правилу Крамера, маємо
![]() .
(97)
.
(97)
Це
співвідношення уявляє собою трансцендентне
рівняння відносно поперечного
хвильового числа ![]() .
.
Якщо задати m та R2/R1, рівняння може бути вирішене чисельно, або графічно. При цому може бути знайдено n його коренів, тому хвиля позначається Еmn.
Аналіз показує, що найнижчим типом хвиль серед хвиль типу Е для ко-аксіалу є хвиля Е01.
Хвилі типу Н коаксіальної лінії - магнітні хвилі.
Вирішення рівняння Гельмгольца знаходяться аналогічно
![]() .
(98)
.
(98)
Гранична
умова (31) для Hz
![]() .
.
Тут напрямок нормалі n - це напрямок r, тому
![]() .
.
Підставляючи вирішення в граничну умову, отримаємо систему лінійних алгебраїчних рівнянь
![]() ,
,
![]() .
.
Знайдемо визначник цієї системи і прирівняємо його нолю


і
звідси отримаємо трансцендентне рівняння
для знаходження значень ![]() .
.
![]() .
(99)
.
(99)
Хвилі типу Н також позначаються Нmn. Найнижчою хвилею є хвиля Н11.
Аналіз
показує, що ![]() .
.
![]() та
та
![]() можливо
знайти по приблизним формулам:
можливо
знайти по приблизним формулам:
![]() ;
;
![]() .
(100)
.
(100)
Структура
поля хвилі Н11
де
в чому нагадує аналогічну структуру
хвилі Н11
колового
хвилеводу

Рисунок 3.3 - Структура е. м. п. хвилі Н11 для коаксіалу
Знаючи критичну довжину хвилі типу Н11 (а це найнижча з хвиль вищого типу для коаксиальної лінії) з'являється можливість визначити критичну частоту коаксіальної ЛП з точки зору виникнення вищих по відношенню до ТЕМ типів хвиль.
![]() ,
звідси
,
звідси ![]()
Підставимо
сюди ![]() з (100)
з (100)
![]()
с
- швидкість світла ![]() мМ/с.
мМ/с.
Приклад:
кабель R1=4мM,
R2=11мМ,
заповнення - поліетилен, ![]() :
:
![]() .
.
В
той же час, зменшивши R1=3мМ,
R2=7мM,
![]() отримаємо
отримаємо
![]() .
.
