
- •1.1 Довідковий матеріал Числові ряди
- •Знакозмінні ряди
- •Степеневі ряди.
- •Розкладання функцій в ряд Тейлора
- •Ряди Фурє
- •2. Ряди Фурє для парних і непарних 2 - періодичних функцій
- •1.2 Аудиторні завдання
- •1.3 Індивідуальні завдання
- •2. Елементи теорії функції комплексної змінної
- •2.1 Довідковий матеріал.
- •2.2 Аудиторні завдання
- •2.3 Індивідуальні завдання
- •3. Елементи операційного числення
- •3.1 Довідковий матеріал.
- •Знаходження зображення за заданим оригіналом
- •Знаходження оригіналу за заданим зображенням
- •Застосування операційного числення
- •Основні оригінали і їх зображення.
- •3.2Аудиторні завдання
- •3.3 Індивідуальні завдання
- •Література
1.2 Аудиторні завдання
1. Дослідити збіжність рядів за необхідною ознакою збіжності:
|
а) |
б) |
в)
|
Відповідь: а) розбіжний, б) може бути збіжним, в) може бути збіжним.
2. Дослідити збіжність числових рядів:
|
а)
|
б)
|
в)
|
г) |
|
д) |
е) |
є) |
|
Відповідь: а) розбіжний, б) розбіжний, в) збіжний, г) збіжний , д) збіжний, е) розбіжний, є) розбіжний.
3. Дослідити збіжність знакозмінних рядів:
-
а)

б)

в)

Відповідь:а) збіжний абсолютно, б) збігається умовно, в) розбіжний.
4. Знайти області збіжності степеневих рядів:
-
а)

б)

в)

г)

Відповідь:
а)(-![]() ;+);
б)
;+);
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Розвинути функцію f(x)=e
 в ряд Тейлора
за степенями x.
в ряд Тейлора
за степенями x.Обчислити інтеграл з точністю до 0,001
![]() .
.
Відповідь: 0,747.
Знайти зазначене число ненульових членів розвинення в ряд розв’язку диференціального рівняння при заданих початкових умовах:
|
|
|
|
(пять членів) |
Відповідь:
у = 2 +![]() (х
+1)
+
(х
+1)
+![]() (х+1)2+
(х+1)2+![]() (х+1)4+
(х+1)4+![]() (х+1)5.
(х+1)5.
Розвинути в ряд Фурє функцію на зазначеному інтервалі
а)![]()
б) f(x)=x2 ; T=2l ; x;
в)
![]() за синусами.
за синусами.
Відповідь:
![]() ;
;
![]() ;
;![]() .
.
1.3 Індивідуальні завдання
1.3.1 Дослідити збіжність ряду за необхідною ознакою збіжності:
|
1.
|
2.
|
3. |
4. |
|
5.
|
6.
|
7. |
8. |
|
9.
|
10. |
11.
|
12.
|
|
13.
|
14.
|
15.
|
16.
|
|
17.
|
18.
|
19.
|
20.
|
|
21.
|
22.
|
23.
|
24. |
|
25.
|
26. |
27. |
28. |
|
29. |
30. |
|
|
1.3.2 Дослідити збіжність числових рядів за допомогою достатніх ознак збіжності:
|
1.а) |
б) |
в) |
г) |
|
2.а) |
б) |
в) |
г) |
|
3.а) |
б) |
в) |
г) |
|
4.а) |
б) |
в) |
г) |
|
5.а) |
б) |
в) |
г) |
|
6.а) |
б) |
в) |
г) |
|
7.а) |
б) |
в) |
г) |
|
8.а) |
б) |
в)
|
г) |
|
9.а) |
б) |
в) |
г) |
|
10.а) |
б) |
в) |
г) |
|
11.а) |
б) |
в) |
г) |
|
12.а) |
б) |
в) |
г) |
|
13.а) |
б) |
в) |
г) |
|
14.а) |
б) |
в) |
г) |
|
15.а) |
б) |
в) |
г) |
|
16а) |
б) |
в) |
г) |
|
17.а) |
б) |
в) |
г) |
|
18.а) |
б) |
в) |
г) |
|
19.а) |
б) |
в) |
г) |
|
20.а) |
б) |
в) |
г) |
|
21.а |
б) |
в) |
г) |
|
22.а) |
б) |
в) |
г) |
|
23.а) |
б) |
в) |
г) |
|
24.а) |
б) |
в)
|
г) |
|
25.а) |
б) |
в) |
г) |
|
26.а) |
б) |
в) |
г) |
|
27.а) |
б) |
в) |
г) |
|
28.а) |
б) |
в) |
г) |
|
29.а) |
б) |
в) |
г) |
|
30.а) |
б) |
в) |
г) |
1.3.3 Дослідити збіжність знакозмінних рядів:
|
1.а) |
б) |
в) |
|
2.а) |
б) |
в) |
|
3.а) |
б) |
в) |
|
4.а) |
б) |
в) |
|
5.а) |
б) |
в) |
|
6.а) |
б) |
в) |
|
7.а) |
б) |
в) |
|
8.
а) |
б) |
в) |
|
9.
а) |
б) |
в) |
|
10.а) |
б) |
в) |
|
11.
а) |
б) |
в) |
|
12.
а) |
б) |
в) |
|
13.а) |
б) |
в) |
|
14.
а) |
б) |
в) |
|
15.
а) |
б) |
в) |
|
16.
а) |
б) |
в) |
|
17.
а) |
б) |
в) |
|
18.
а) |
б) |
в) |
|
19.
а) |
б) |
в) |
|
20.
а) |
б) |
в) |
|
21.
а) |
б) |
в)
|
|
22.
а) |
б) |
в) |
|
23.а) |
б) |
в) |
|
24.а) |
б) |
в) |
|
25.а) |
б) |
в)
|
|
26.а) |
б) |
в) |
|
27.а)
|
б) |
в) |
|
28.а) |
б)
|
в) |
|
29.а) |
б) |
в) |
|
30.а) |
б) |
в) |
1.3.4 Знайти області збіжності степеневих рядів:
|
1.а)
|
б) |
в) |
|
2.а) |
б) |
в) |
|
3.а) |
б) |
в) |
|
4.а) |
б) |
в) |
|
5.а) |
б) |
в) |
|
6.а) |
б) |
в) |
|
7.а) |
б) |
в) |
|
8.а)
|
б) |
в) |
|
9.а) |
б) |
в) |
|
10.а) |
б) |
в) |
|
11.а) |
б) |
в) |
|
12.а) |
б) |
в) |
|
13.а) |
б) |
в) |
|
14.а) |
б) |
в) |
|
15.а) |
б) |
в) |
|
16.а) |
б) |
в) |
|
17.а) |
б) |
в) |
|
18.а) |
б) |
в) |
|
19.а) |
б) |
в) |
|
20.а) |
б)
|
в) |
|
21.а) |
б) |
в) |
|
22.а) |
б) |
в) |
|
23.а) |
б) |
в) |
|
24.а) |
б) |
в) |
|
25.а) |
б) |
в) |
|
26.а) |
б)
|
в) |
|
27.а) |
б) |
в) |
|
28.а) |
б)
|
в) |
|
29.а) |
б) |
в) |
|
30.а) |
б) |
в) |
1.3.5 Обчислити інтеграл з точністю до 0,001:
|
1.
|
2. |
3. |
|
4.
|
5. |
6.
|
|
7.
|
8
|
9.
|
|
10.
|
11. |
12.
|
|
13. |
14. |
15.
|
|
16.
|
17. |
18.
|
|
19.
|
20.
|
21.
|
|
22.
|
23.
|
24.
|
|
25.
|
26.
|
27.
|
|
28
|
29.
|
30.
|
1.3.6 Знайти зазначене число ненульових членів розвинення в ряд розв’язку диференціального рівняння при заданих початкових умовах:
|
1. |
|
|
(чотири члени) |
| |||
|
2. |
|
|
(три члени) | ||||
|
3. |
|
|
(чотири члени) | ||||
|
4. |
|
|
(чотири члени) | ||||
|
5. |
|
|
(три члени) | ||||
|
6. |
|
|
(чотири члени) | ||||
|
7. |
|
|
(чотири члени) | ||||
|
8. |
|
|
(чотири члени) | ||||
|
9. |
|
|
(три члени) | ||||
|
10. |
|
|
(три члени ) | ||||
|
11. |
|
|
(чотири члени) | ||||
|
12. |
|
|
(чотири члени) | ||||
|
13. |
|
|
(три члени) | ||||
|
14. |
|
|
(чотири члени) | ||||
|
15. |
|
|
(чотири члени) | ||||
|
16. |
|
|
(три члени) | ||||
|
17. |
|
|
(три члени) | ||||
|
18. |
|
|
(три члени) | ||||
|
19. |
|
|
(чотири члени) | ||||
|
20. |
|
|
(чотири члени) | ||||
|
21. |
|
|
(три члени) | ||||
|
22. |
|
|
(чотири члени) | ||||
|
23. |
|
|
(три члени) | ||||
|
24. |
|
|
(три члени) | ||||
|
25. |
|
|
(чотири члени) | ||||
|
26. |
|
|
(три члени) | ||||
|
27. |
|
|
(три члени) | ||||
|
28. |
|
|
(чотири члени) | ||||
|
29. |
|
|
(чотири члени) | ||||
|
30. |
|
|
(чотири члени) | ||||
1.3.7 Розкласти в ряд Фурє
а)
функцію
![]() =
=![]() з періодом
з періодом![]() ;
;
б)
функцію
![]() задану на інтервалі
задану на інтервалі![]() ;
;
в)
функцію
![]() задану на інтервалі
задану на інтервалі![]() (в прикладах з непарними номерами по
косинусам, в прикладах з парними номерами
по синусам).
(в прикладах з непарними номерами по
косинусам, в прикладах з парними номерами
по синусам).
|
1.
|
|
|
|
2.
|
|
|
|
3.
|
|
|
|
4.
|
|
|
|
5.
|
|
|
|
6.
|
|
|
|
7.
|
|
|
|
8.
|
|
|
|
9.
|
|
|
|
10.
|
|
|
|
11.
|
|
|
|
12.
|
|
|
|
13.
|
|
|
|
14.
|
|
|
|
15.
|
|
|
|
16.
|
|
|
|
17.
|
|
|
|
18.
|
|
|
|
19.
|
|
|
|
20.
|
|
|
|
21.
|
|
|
|
22.
|
|
|
|
23.
|
|
|
|
24.
|
|
|
|
25.
|
|
|
|
26.
|
|
|
|
27.
|
|
|
|
28.
|
|
|
|
29.
|
|
|
|
30.
|
|
|

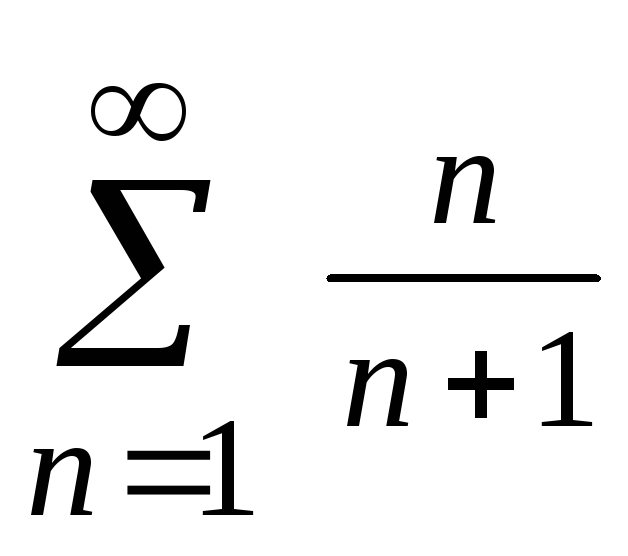




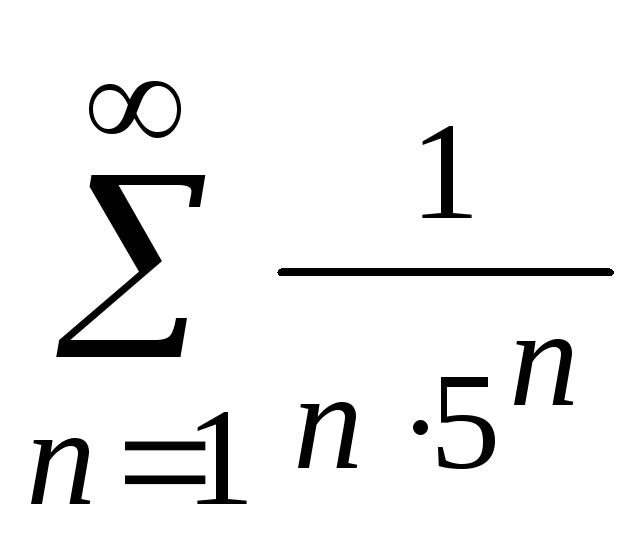





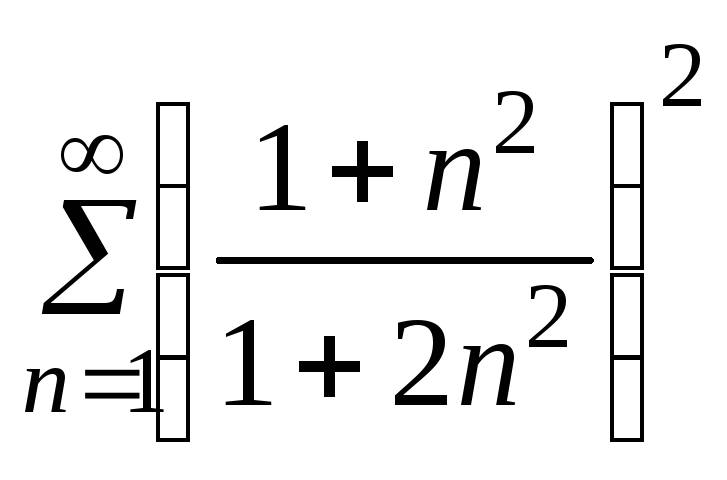









 .
. .
. .
. .
. .
.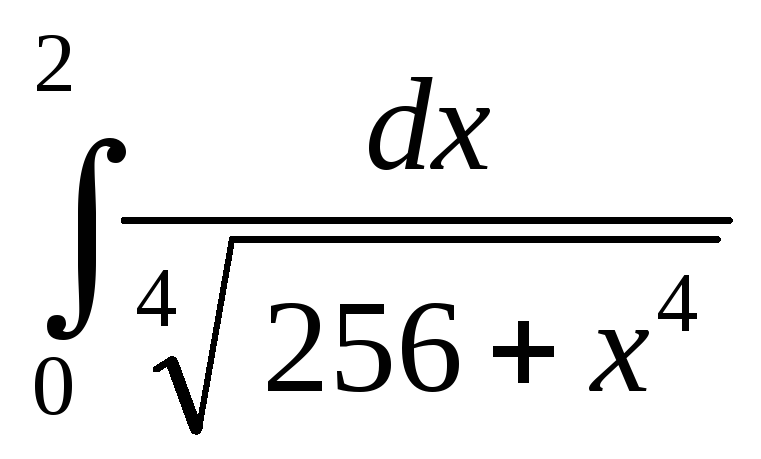 .
. .
. .
.