Тема 2. Решение граничных задач при помощи степенных рядов.

§ 1. О рядах Фурье в комплексной форме.

Пусть – действительная функция, заданная на отрезкеи удовлетворяющая на нем условиям Дирихле (функциянепрерывна на отрезке за возможным исключением конечного числа разрывов первого рода и имеет конечное число максимумов и минимумов). В этом случае функциюможно представить рядом Фурье

,

где

, .

Напомним, что ряд Фурье сходится во всех точках интервала к функции, которая совпадает св точках непрерывности. На концах 0 ипромежутка суммой ряда оказывается число. Еслиявляется непрерывной во всех точках отрезка, удовлетворяет на нем условиям Дирихле и, то ряд Фурье сходится кравномерно на отрезке.

Заменим в ряде Фурье иизвестными выражениями

, ,

получим

.

После введенных новых обозначений

будем иметь

. (1.1)

Этот ряд будем называть комплексным рядом Фурье функции .

Получим выражения коэффициентов комплексного ряда через функцию . С этой целью воспользуемся тем, что для целого

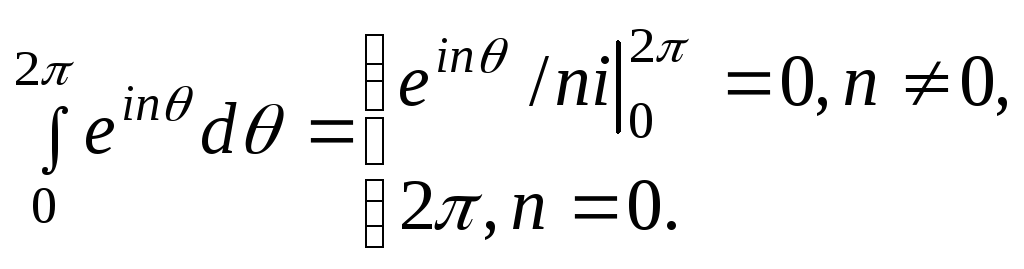
Умножим обе части формулы (1.1) на и проинтегрируем поот 0 до, получим:

.

Следовательно,

(1.2)

Рассмотрим теперь комплексную функцию , гдеи– действительные функции, удовлетворяющие условиям Дирихле на. Каждую из этих функций можно представить комплексным рядом Фурье вида (1.1). Умножив ряд для функциинаи прибавив его к ряду для функции, получим снова ряд вида (1.1)

, (1.3)

в котором согласно (1.2)

(1.4)

В отличие от предыдущего случая коэффициенты , ряда (1.4) не являются комплексно сопряженными числами.

Если действительная функция непрерывна и имеет непрерывные производные на отрезкедо порядкаи производная порядкаудовлетворяет условиям Дирихле на том же промежутке, то коэффициенты, ряда Фурье функции удовлетворяют неравенствам

, ,,

где – некоторая положительная постоянная. Отсюда вытекает, что коэффициентыряда (1.3) для функцииудовлетворяют неравенствам того же вида

при условии, что функции иимеют непрерывные производные до порядкана, а их производные порядкаудовлетворяют условиям Дирихле.

Заметим, что при , то есть когда функциииимеют непрерывные производные, удовлетворяющие условиям Дирихле, для коэффициентовкомплексного ряда Фурье (1.3) выполняются неравенства

А это означает, что ряд (1.3) сходится абсолютно, так как

и ряд сходится.

§ 2. Решение первой граничной задачи для круга.

Искомые функции ив случае первой граничной задачи плоской теории упругости должны на границе круга удовлетворять граничному условию

,

гдеи– известные по условию задачи функции точек границыкруга,– произвольная комплексная константа,,,– предельные значения аналитических в кругефункций,,при. Известно, что, не нарушая напряженного состояния тела, можно распорядиться выбором следующих величин,,или . Условимся считать,,.

Функции и, как аналитические в круге, могут быть единственным образом разложены в степенные ряды вида

, .

Но тогда

, ,.

Предположим, что эти ряды сходятся не только внутри круга, но и на его границе :. Внесём их в граничное условие задачи, получим

.

На окружности . Подставим эти выражения дляив граничное условие и представим функциюрядом Фурье

.

Напомним, что коэффициенты этого ряда представляются формулами (1.2). Считая коэффициенты в дальнейшем известными величинами, так как функцияизвестна по условию задачи. Выполнив указанные действия, придем к равенству

.

Сравнивая коэффициенты при , получаем уравнение

или . (2.1)

Сравнивая коэффициенты при , получаем

(2.2)

Наконец, сравнивая коэффициенты при, получаем

(2.3)

Искомые коэффициенты разложений функций ив степенные ряды удовлетворяют системе уравнений (2.1)-(2.3).

В левой части уравнения (2.1) находится действительная величина. Поэтому равенство (2.1) возможно только в том случае, когда величина действительна. В монографии [] показано, что коэффициентбудет действительным, если сумма моментов всех внешних сил относительно центра круга рана нулю. Во всех граничных задачах теории упругости, которые мы рассматриваем, всегда предполагается, что под действием приложенных нагрузок упругое тело находится в равновесии. Поэтому в рассматриваемых задачах коэффициент– действительное число. Из уравнения (2.1) вытекает, что– неопределенная величина, а

.

Поскольку в круге функция, то ясно, что. Мнимая часть производнойпо соглашению в начале параграфа равна нулю, следовательно,. Поэтому

. (2.4)

Коэффициентыв разложениив степенной ряд легко определяются из уравнений (2.2)

. (2.5)

Коэффициенты степенного ряда длянаходим из уравнений (2.3) (в которых нужно заменить все величины сопряженными)

. (2.6)

Теперь, когда коэффициенты степенных рядов для функций истали известны, по формулам

, (2.7)

можно формально построить эти функции в круге , затем по формулам Колосова- Мусхелишвили определить напряжения и перемещения в упругом теле. В монографии [] показано, что описанный способ решения первой граничной задачи дает верное решение, если координаты вектора напряжения, задаваемого на границе круга, имеют первые производные по, которые удовлетворяют условиям Дирихле.

Подводя итог сказанному, кратко опишем последовательность решения первой граничной задачи теории упругости для круга.

1. Определяем в каждой точке границы круга координаты вектора напряжения. Проверяем, выполняются ли условия равновесия тела:.

2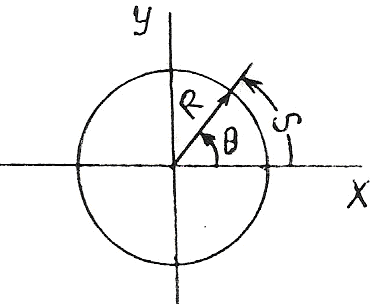. Строим комплексную функцию, руководствуясь формулой

.

3. Разлагаем функцию в комплексный ряд Фурье

, .

4. Определяем коэффициенты степенных рядов для функций,при помощи формул (2.4)-(2.6), а затем строим функцииипо формулам (2.7).

5. Определяем напряжения в круге при помощи формул Колосова- Мусхелишвили

, .

6. Определяем перемещения иточек упругого тела, руководствуясь формулой

.

Решение второй граничной задачи аналогично решению первой. Во второй граничной задаче аналитические в круге функцииидолжны удовлетворять на его границе условию (9.1):

. (2.8)

В центре круга можно положить . Функцию,, известную по условию задачи, представим комплексным рядом Фурье

.

Предположив, что степенные ряды (2.7), (2.8) для функций исходятся не только внутри круга, но и на его границе, внесем их в граничное условие(2.8) задачи. Придем в конечном итоге к равенству

,

из которого несложно определить все коэффициенты рядов(2.7) для и. При помощи формул Колосова-Мусхелишвили по найденным функциями найдём напряжения и перемещения в упругом теле. Полученное таким образом решение будет удовлетворять всем условиям второй граничной задачи, то есть будет истинным, если функция имеет непрерывную производную, удовлетворяющая условиям Дирихле.

П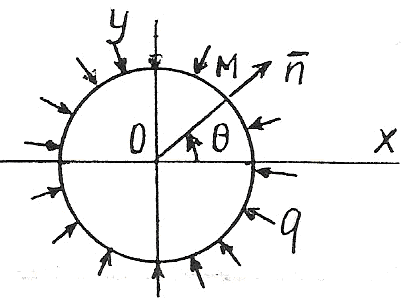ример. Определить напряжения и перемещения в круге , на границу которого действует давление интенсивности.

Решение. Определим координаты вектора напряжения в произвольной точкеграницы круга. Пусть эта точка характеризуется угловой координатой, тогда координаты единичного векторав точке, нормального к границе круга и направленного во внешнюю сторону тела, будут таковы,. Пусть– длина малой окрестности границы точки. Главный вектор нагрузки, действующий на эту окрестность, равен. Согласно определению

.

Следовательно, .

Легко проверить, что под действием давления тело находится в состоянии равновесия. Действительно, разбив границу на большое количество малых частейи, приняв во внимание, что нагрузка, действующая на часть, эквивалентна силе, где, будем иметь

,

.

Так как плечо каждой силы относительно центра кругаравно нулю, то

.

Итак, условия равновесия тела выполняются, поэтому можно продолжить решение задачи.

Определим комплексную функцию :

.

Найдем коэффициенты разложения функции в комплексный ряд Фурье по степеням. Очевидно, что

.

По формулам (2.4)-(2.6) определим коэффициенты степенных рядов для функций и

,

.

Таким образом, согласно формулам (2.7)

.

Определим напряжения и перемещенияи в круге при помощи формул Колосова- Мусхелишвили. Имеем

,

,

.

Отсюда получаем

,

Отбрасывая в выражении для член , характеризующий смещения всех точек диска на одно и тоже расстояние вдоль оси (он не влияет на напряжение в теле), получим окончательное выражение искомых величин

.

Из этих формул вытекает, что при равномерном сжатии круглого упругого диска давлением напряжения ив каждой его точке являются сжимающими, они не зависят от выбора направления осейидекартовой системы координат. Перемещения точек тела являются радиальными, пропорциональными их расстояниям до центра круга. Эти выводы полностью соответствуют физической картине деформации диска.