Розділ 8. Наближене розв’язання крайової задачі для звичайних диференціальних рівнянь

8.1. Метод Гальоркіна

Нехай дана крайова задача

, (1)

(2)

Для знаходження наближеного розв’язку цієї задачі вчинимо так. Задаємося на деякою системою лінійно-незалежних функцій, неперервних і двічі неперервно-диференційованих. Причому функціяповинна задовольняти неоднорідним крайовим умовам (2), аповинні задовольняти однорідним крайовим умовам, тобто крайовим умовам

(3)

Одним із способів вибору базисних функцій на основі многочленів є наступний. Як візьмемо лінійну функцію

, (4)

коефіцієнти якої підберемо так, щоб вона задовольняла неоднорідним крайовим умовам (2), тобто з лінійної алгебраїчної системи

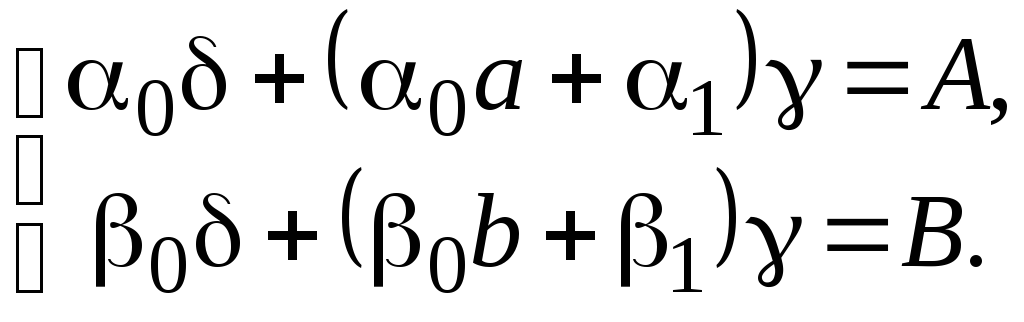(5)

Функції приможна взяти однопараметричними виду

, (6)

якщо в (3) , або виду

(7)

у самому загальному випадку. Очевидно, що при будь-яких ці функції задовольняють першому з рівностей (3) (окрім випадку, тоді першому з рівностей (3) не задовольняє одна функція –), а якщо зафіксувати

(8)

у виразі (6) і

(9)

у (7), то вони будуть задовольняти і другому з рівнянь (3).

Розглянемо функцію як лінійну комбінацію

(10)

де – невідомі константи.

Якщо базисні функції вибрати так, як це було описано вище, то буде задовольняти крайовим умовам (2), незалежно від вибору.

Розглянемо функцію . Вона називається відхилом і отримується при підстановці в рівняння (1) виразу (3). Якщо відхил дорівнює нулю, то маємо випадок точного розв’язоку. Задача розв’язання звичайного диференціального рівняння зводиться до того, щоб відхил був мінімальним. Тоді вираз (10) буде наближеним розв’язком задачі.

Підбір коефіцієнтів породжує різні методи.

Суть методу Гальоркіна полягає в тому, що базисні функції повинні бути ортогональні до відхилу.

Умова ортогональності двох функцій має вигляд:

,

В результаті одержимо систему лінійних алгебраїчних рівнянь щодо невідомих коефіцієнтів . Знайшовши ці коефіцієнти і підставивши їх у (10), одержимо наближений розв’язок крайової задачі.

Приклад. Методом Гальоркіна знайти наближений розв’язок рівняння , що задовольняє крайовим умовам.

Розв’язок. За систему базисних функцій обираємо функції .

Наближений розв’язок задачі шукаємо у вигляді полінома

.

Підставляючи в ліву частину заданого диференціального рівняння, одержуємо відхил:

.

Умови ортогональності функції до функційприводять до системи

Підставляючи замість її значення, після відповідного інтегрування одержуємо систему

.

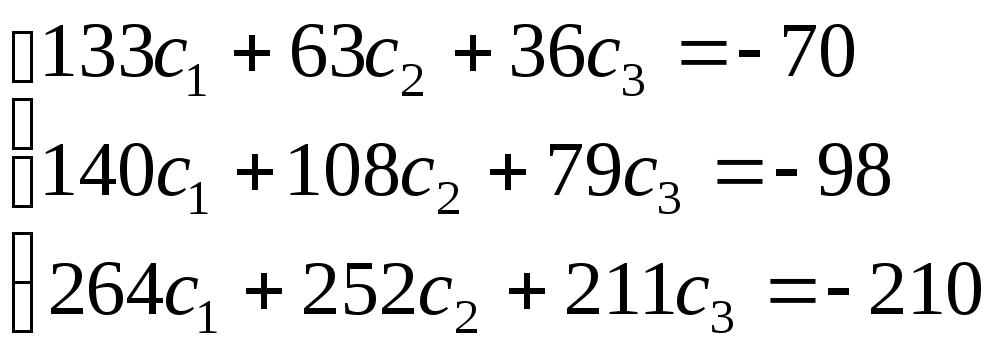Звідси знаходимо: ;,, і, отже,– наближений розв’язок крайової задачі. Похибка наближеного розв’язку залежить від кількості базисних функцій.

Питання для самоперевірки

1. Які існують типи крайових умов?

2. В чому полягає метод Гальоркіна? Що таке відхил?

3. В чому полягають принципи підбору базисних функцій?

4. Від чого залежить похибка методу Гальоркіна?

8.2. Метод кінцевих різниць

Розглянемо лінійне диференціальне рівняння 2-го порядку із змінними коефіцієнтами

(1)

де ,,неперервні функції на,- сталі, такі, що. Розіб'ємо відрізокнаn рівних частин, тобто одержимо ; побудуємо систему рівновіддалених вузлів

.

Розв’язок задачі будемо шукати чисельно. Для цього в рівнянні (1) похідні замінимо кінцевими різницями другого порядку точності.

Введемо позначення ,,,.

Одержимо:

. (2)

Граничні умови запишемо в такому вигляді:

. (3)

Таким чином одержимо систему рівнянь зневідомими. Розв’язуючи цю систему, знайдемо значення функціїу відповідних точках.

На рис. 12 наведено блок-схему програми розв’язку крайової задачі методом кінцевих різниць.

У даній блок-схемі: n – кількість відрізків розбиття, a, b – ліва та права границя відрізку, α₀, β₀, α₁, β₁, A, B – сталі з крайових умов, h – крок розбиття, x(0),…,x(n) – система рівновіддалених точок, y(0),…,y(n) – наближені значення розв’язку крайової задачі, p(x(i)), q(x(i)), f(x(i)) – значення функцій p(x), q(x), f(x) з диференційного рівняння у точці x(i), gauss(a,m,b,y) – підпрограма розв’язку системи лінійних алгебраїчних рівнянь методом Гауса (a – матриця сталих коефіцієнтів, m – кількість рівнянь, b – вектор-стовпець вільних членів, y – вектор-стовпець невідомих).

Приклад. Методом кінцевих різниць знайти розв’язок крайової задачі:

.

Розв’язок. Виберемо крок . Поклавши, з огляду на симетрію рівняння і крайових умов будемо мати. Таким чином, потрібно визначити лише дві ординати:і. Запишемо рівняння (2) у вигляді

.

При , тобто прибудемо мати

.

Аналогічно при , тобто прибудемо мати

.

З огляду на і використовуючи крайову умову, маємо систему

.

Звідси ;.

Отримані значення занесемо в таблицю

	0	1	2	3	4
	-1	-0,5	0	0,5	1
	0	0,721	0,967	0,721	0