
- •Розділ 6. Прямі методи розв’язання систем лінійних алгебраїчних рівнянь. Метод гауса
- •Питання для самоперевірки
- •Завдання до лабораторної роботи № 4
- •Варіанти завдань
- •Розділ 6. Наближені методи розв’язання систем лінійних алгебраїчних рівнянь
- •6.1. Метод простих ітерацій
- •Питання для самоперевірки
- •2.2. Метод Зейделя
- •Завдання до лабораторної роботи № 5
- •Варіанти завдань
- •Завдання до лабораторної роботи № 6
- •Розділ 7. Чисельне розв’язання нелінійних алгебраїчних і трансцендентних рівнянь та їх систем
- •7.1. Загальні положення
- •7.2. Метод Ньютона (дотичних)
- •Питання для самоперевірки
- •7.3. Метод пропорційних частин (хорд)
- •7.4. Метод градієнтного спуску
- •Питання для самоперевірки
- •Завдання до лабораторної роботи № 7
- •Завдання до лабораторної роботи № 8
- •Індивідуальне завдання № 3
- •Варіанти завдань
- •Розділ 8. Наближене розв’язання крайової задачі для звичайних диференціальних рівнянь
- •8.1. Метод Гальоркіна
- •Наближений розв’язок задачі шукаємо у вигляді полінома
- •Питання для самоперевірки
- •8.2. Метод кінцевих різниць
- •Питання для самоперевірки
- •Завдання до лабораторної роботи № 9
- •Індивідуальне завдання № 4
7.4. Метод градієнтного спуску
Нехай маємо систему рівнянь
![]()
![]() (1)
(1)
чи в матричній формі
![]() , (2)
, (2)
де
![]() ,
,![]() .
.
Припустимо, що функції
![]() дійсні й неперервно-диференційовані в
їхній загальній області визначення.
Розглянемо функцію
дійсні й неперервно-диференційовані в
їхній загальній області визначення.
Розглянемо функцію
![]() . (3)
. (3)
Очевидно, що кожний розв’язок
системи (1) перетворює на нуль функцію
![]() ;
навпаки, числа
;
навпаки, числа![]() ,
для яких функція
,
для яких функція![]() дорівнює нулю, є коренями системи (1).
Таким чином, задача зводиться до
знаходження мінімуму скалярної функції
багатьох змінних
дорівнює нулю, є коренями системи (1).
Таким чином, задача зводиться до
знаходження мінімуму скалярної функції
багатьох змінних![]() .
.
Одним з методів мінімізації
функцій багатьох змінних є метод
градієнтного спуску. Якщо
![]() – деяке наближення до розв’язку системи,
то в методі градієнтного спуску ми
одержуємо нове наближення
– деяке наближення до розв’язку системи,
то в методі градієнтного спуску ми
одержуємо нове наближення![]() ,
рухаючись за напрямком найбільшої
миттєвої швидкості зміни функції
,
рухаючись за напрямком найбільшої
миттєвої швидкості зміни функції![]() в точці
в точці![]() до точки, де значення
до точки, де значення![]() мінімальне, тобто
мінімальне, тобто
![]() , (4)
, (4)
де
![]() вибирається з умови мінімуму
вибирається з умови мінімуму![]() .
.
Якщо
![]() – мала величина, квадратом і вищими
ступенями якої можна знехтувати, то,
розкладаючи функції
– мала величина, квадратом і вищими
ступенями якої можна знехтувати, то,
розкладаючи функції![]() за степенями
за степенями![]() з точністю до лінійних членів і виражаючи
з точністю до лінійних членів і виражаючи![]() через матрицю Якобі
через матрицю Якобі![]() ,
одержимо таке представлення розрахункової
формули методу градієнтного спуску
,
одержимо таке представлення розрахункової
формули методу градієнтного спуску
![]() , (5)
, (5)
де
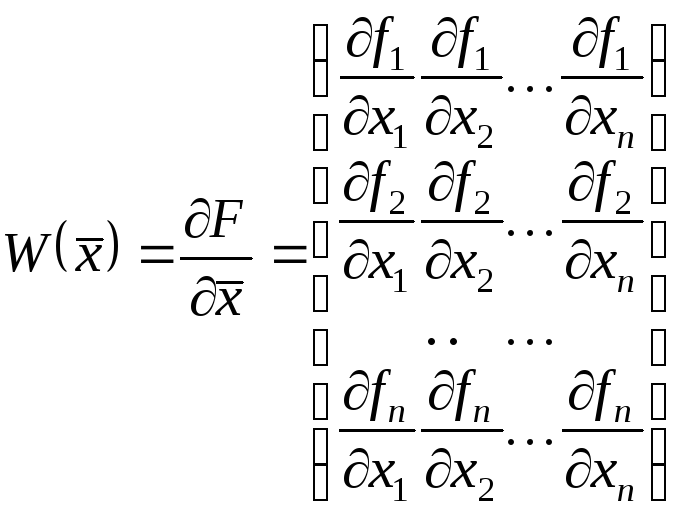 матриця Якобі вектор-функції
матриця Якобі вектор-функції![]() .
.
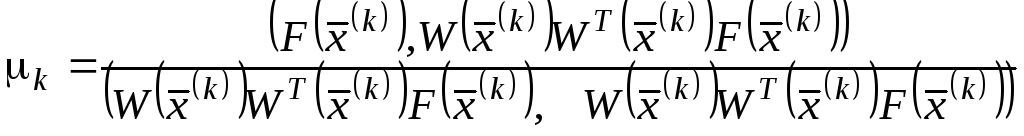 . (6)
. (6)
Слід зазначити, що ітераційний
процес, побудований за методом градієнтного
спуску, збігається до точного розв’язку,
якщо початкове наближення
![]() обране з досить малого околу кореня.
обране з досить малого околу кореня.
На рис. 11 наведено блок-схему програми розв’язку нелінійних систем методом градієнтного спуску.
У даній блок-схемі: n – кількість рівнянь у системі, x(1),…,x(n) – наближені значення розв’язку системи; ε – точність обчислень; k – номер ітерації; f(i), fi(x(1),…,x(n)) – значення, що приймає ліва частина i-го рівняння системи у точці (x(1),…,x(n)); w(i;j), wij(x(1),…,x(n)) – значення коефіцієнтів матриці Якобі у точці (x(1),…,x(n)); trans(w,n,m,wt) – підпрограма транспонування матриці (w – вихідна матриця, n – кількість рядків вихідної матриці, m – кількість стовпців матриці, wt – транспонована матриця); ummat(w,n,m,l,wt,wwt) – підпрограма добутку двох матриць (w – перша матриця, n – кількість рядків першої матриці, m – кількість стовпців першої та рядків другої матриці, l – кількість стовпців другої матриці, wt – друга матриця, wwt – добуток двох матриць).

Приклад.
Методом градієнтного спуску приблизно обчислити корені системи

розташовані в околі початку координат.
Розв’язок.
Маємо
![]() .
.
Тут
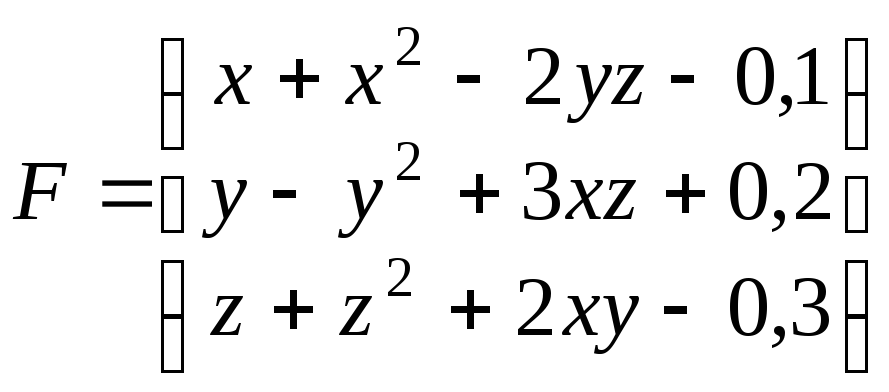 і
і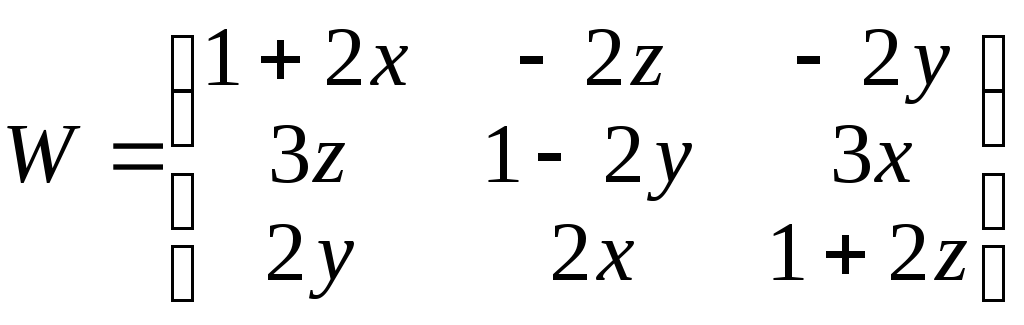 .
.
Підставляючи нульове наближення, будемо мати:
![]() і
і
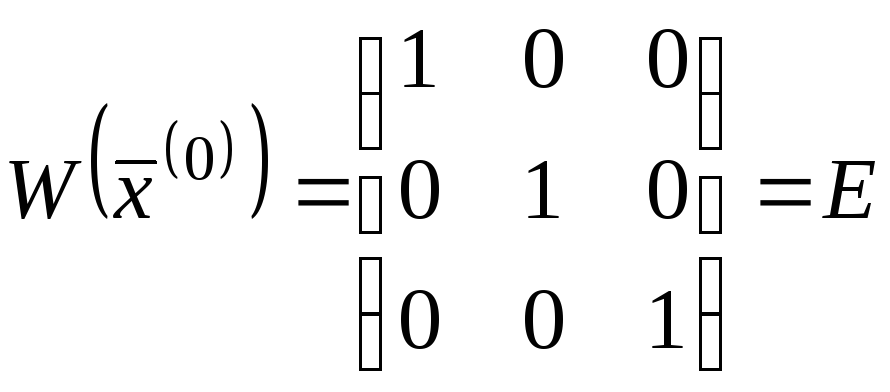
За формулами (5) і (6) одержуємо перше наближення
 і
і
![]()
Аналогічно знаходимо друге
наближення
![]() .
.
Маємо:
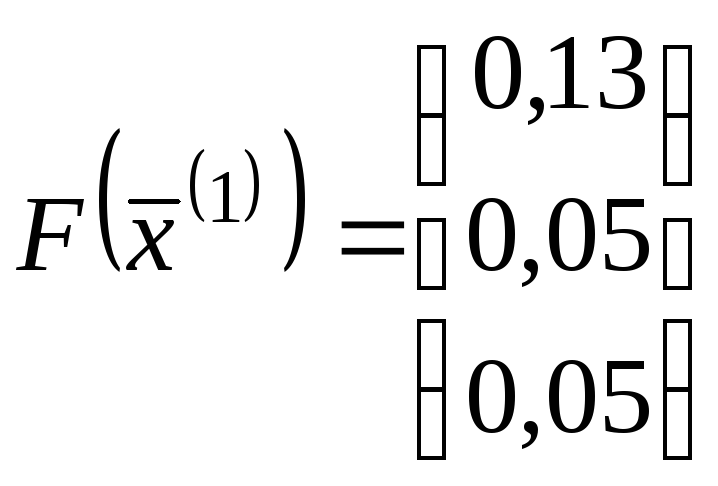 ,
,

Звідси:
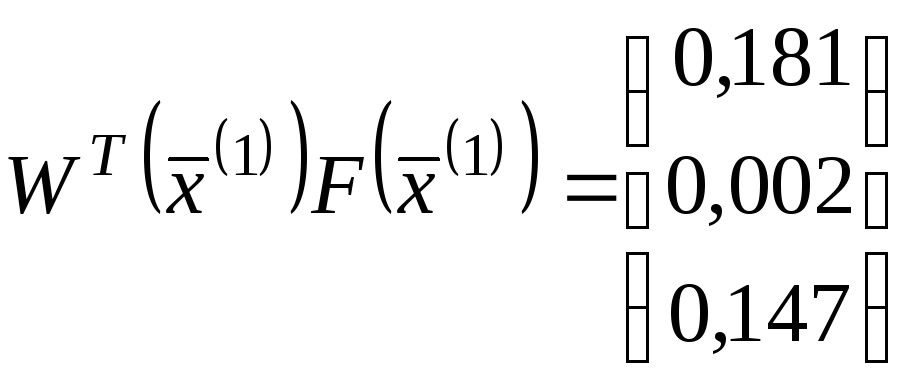 та
та
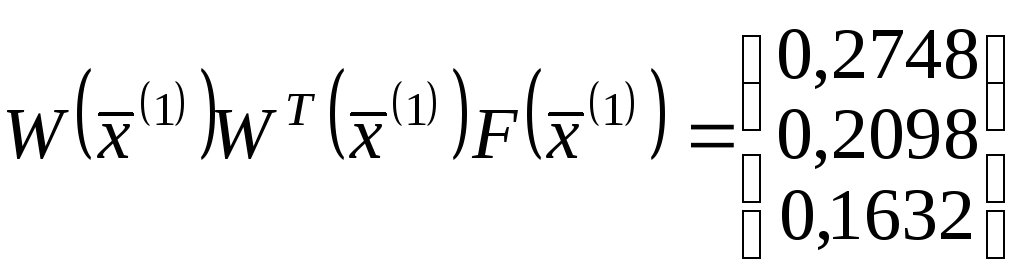
Отже,
![]() і
і
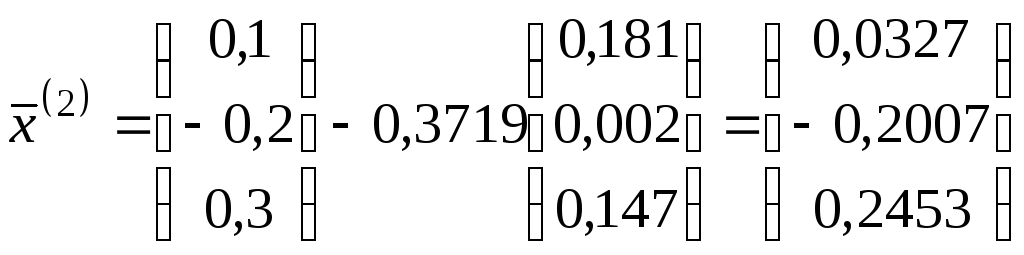 .
.
Для контролю обчислимо відхил
 .
.
Питання для самоперевірки
Сформулюйте постановку задачі, опишіть метод розв’язання.
В чому полягає основна ідея методу градієнтного спуска?
Які умови закінчення ітераційного процесу?
Що може відбутися при невдалому виборі нульового наближення?
Дайте геометричну інтерпретацію методу.
Завдання до лабораторної роботи № 7
Методом Ньютона з точністю
до
![]() обчисліть всі дійсні корені рівняння
обчисліть всі дійсні корені рівняння
![]() .
.
Значення коефіцієнтів
![]()
![]() вибираються з таблиці варіантів. Номер
варіанта, що являє собою двозначне
число, задається викладачем. Перша цифра
номера варіанта визначає значення шифру
по вертикалі, друга – по горизонталі.
вибираються з таблиці варіантів. Номер
варіанта, що являє собою двозначне
число, задається викладачем. Перша цифра
номера варіанта визначає значення шифру
по вертикалі, друга – по горизонталі.
|
Шифр по вертикалі |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
1,6 |
-2,4 |
0,8 |
3,6 |
-1,2 |
6,4 |
-2,8 |
1,2 |
-0,4 |
5,2 |
|
Кое-фіцієнт
|
Шифр по горизонталі
| |||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 | |
|
|
5,1 |
3,3 |
-6,3 |
-1,5 |
5,7 |
6,3 |
1,2 |
-6,9 |
5,4 |
-2,1 |
|
|
0,2 |
0 |
0,8 |
0 |
-1,2 |
0,4 |
0 |
-0,6 |
1,0 |
0 |
|
|
-2 |
3 |
7 |
-1 |
-4 |
6 |
-3 |
8 |
9 |
-5 |
