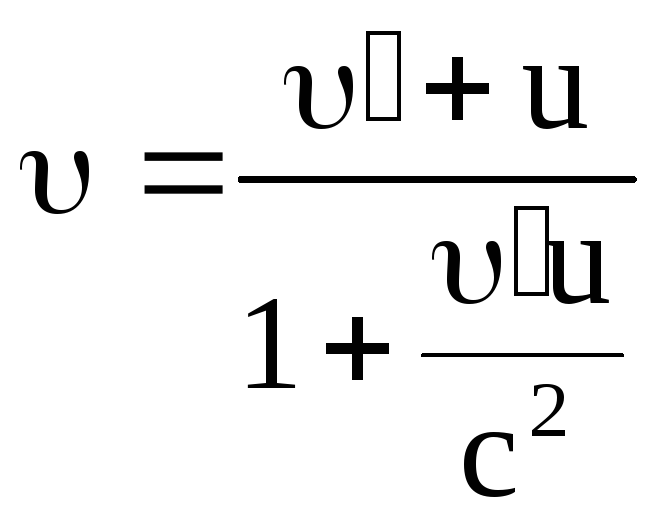-
Постулати ейнштейна. Перетворення лоренца
Для
пояснення дослідних результатів та
ряду інших утруднень у фізиці в 1905 р.
А.Ейнштейн створив нову механіку, яка
дістала назву спеціальної
теорії відносності
(СТВ).
Термін „спеціальна” підкреслює те, що
ця теорія розглядає явища тільки
в інерціальних системах відліку.
Для відносно великих (![]() )
швидкостей руху закони класичної
механіки треба заміняти більш загальними
законами теорії відносності.
)
швидкостей руху закони класичної
механіки треба заміняти більш загальними
законами теорії відносності.
Значний вклад у розробку СТВ внесли Х.Лоренц, А.Пуанкаре, Г.Мінковський. Аналізуючи основи класичної механіки Ньютона Ейнштейн прийшов до висновку, що уявлення про абсолютні простір і час є неправильними. У СТВ простір і час органічно пов’язані між собою і з рухом матерії, є двома сторонами одного цілого.
В основі теорії відносності (Ейнштейн, 1905) лежать два постулати — твердження, котрі приймаються без доказів, хоча, на відміну від аксіом, вони можуть не бути самоочевидними. Ці постулати належать Ейнштейну:
-
Всі закони фізики є однаковими в інерціальних системах відліку.
-
Величина швидкості світла у вакуумі
 є граничною величиною для швидкості,
яку не можна перевищити жодним переносом
енергії, ані у вигляді хвилі, ані у формі
руху матеріального тіла.
є граничною величиною для швидкості,
яку не можна перевищити жодним переносом
енергії, ані у вигляді хвилі, ані у формі
руху матеріального тіла.
Перший постулат Ейнштейна узагальнює принцип відносності Галілея з механічних явищ на всі фізичні явища. Не лише закони механіки, а загалом всі фізичні закони однакові в кожній з інерціальних систем відліку.
Другий
постулат Ейнштейна отримав експериментальне
підтвердження в оптичних дослідах
Майкельсона
(1900). Він показав експериментально, що
швидкість розповсюдження світла у
вакуумі лишається незмінною, незалежно
від того з якою швидкістю
![]() рухається джерело цього світла. Майкельсон
використав швидкість руху Землі (
рухається джерело цього світла. Майкельсон
використав швидкість руху Землі (![]() ),
як планети, і переконався, що світло
випущене з поверхні Землі рухається з
однаковою швидкістю як в напрямі руху
планети, так і в протилежному напрямі.
Отже, класичний закон складання
швидкостей (1.10.4), який передбачає, що ці
швидкості нібито мусили бути різними
(у першому випадку (
),
як планети, і переконався, що світло
випущене з поверхні Землі рухається з
однаковою швидкістю як в напрямі руху
планети, так і в протилежному напрямі.
Отже, класичний закон складання
швидкостей (1.10.4), який передбачає, що ці
швидкості нібито мусили бути різними
(у першому випадку (![]() ),
а у другому відповідно (
),
а у другому відповідно (![]() ))
не відповідає дійсності при таких
швидкостях.
))
не відповідає дійсності при таких
швидкостях.
Як же обійшли фізики це утруднення? Відповідь на це питання буде наведена нижче.
Р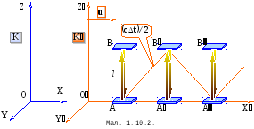 озглянемо
такий уявний
експеримент.
Нехай, в нашому розпорядженні є пристрій,
що складається з жорсткого стержня, на
кінцях якого розміщено два плоских
дзеркала, повернутих відбиваючими
поверхнями одна до одної (Мал. 1.10.2). Між
дзеркалами пробігає короткий світловий
імпульс. Період, за який світловий
імпульс пробігає від дзеркала А
до В
і знову до А
дорівнює часовому інтервалу між двома
послідовними моментами досягнення
світловим імпульсом певного дзеркала.
Нехай пристрій (стержень з дзеркалами)
розмішено нерухомо в системі К’
і орієнтовано перпендикулярно до напряму
руху системи К’
відносно системи К.
Інерціальні системи відліку рухаються
одна відносно одної з швидкістю
озглянемо
такий уявний
експеримент.
Нехай, в нашому розпорядженні є пристрій,
що складається з жорсткого стержня, на
кінцях якого розміщено два плоских
дзеркала, повернутих відбиваючими
поверхнями одна до одної (Мал. 1.10.2). Між
дзеркалами пробігає короткий світловий
імпульс. Період, за який світловий
імпульс пробігає від дзеркала А
до В
і знову до А
дорівнює часовому інтервалу між двома
послідовними моментами досягнення
світловим імпульсом певного дзеркала.
Нехай пристрій (стержень з дзеркалами)
розмішено нерухомо в системі К’
і орієнтовано перпендикулярно до напряму
руху системи К’
відносно системи К.
Інерціальні системи відліку рухаються
одна відносно одної з швидкістю
![]() .
.
Проаналізуємо
рух світлового променя між дзеркалами
в системах К’
і К.
В системі К’
пристрій нерухомий, отже, імпульс подолає
відстань від А
до В
і знову до А
за час
![]() =
=![]() ,
тобто за період. В системі К
відстань між дзеркалами також буде не
змінюватися і дорівнюватиме
,
тобто за період. В системі К
відстань між дзеркалами також буде не
змінюватися і дорівнюватиме
![]() .
Проте, шлях світлового імпульсу протягом
періоду світлового імпульсу буде іншим
(ламана лінія АВ’А”).
Світловий імпульс пройде вже більший
шлях з тією самою швидкістю
.
Проте, шлях світлового імпульсу протягом
періоду світлового імпульсу буде іншим
(ламана лінія АВ’А”).
Світловий імпульс пройде вже більший
шлях з тією самою швидкістю
![]() .
З трикутника
.
З трикутника
![]() АВ’А’
видно, що в цьому випадку:
АВ’А’
видно, що в цьому випадку:
|
|
(1.10.5) |
звідки:
|
|
(1.10.6) |
враховуючи,
що
![]() =
=![]() ,
дістанемо:
,
дістанемо:
|
|
(1.10.7) |
![]()
 -
швидкість пристрою в системі К. З (1.10.7)
випливає, що
-
швидкість пристрою в системі К. З (1.10.7)
випливає, що
![]()
![]()
![]() .
Отже, годинники
у різних системах відліку йдуть
по-різному.
В системі К
відносно якої пристрій рухається,
годинник буде йти повільніше, ніж в
системі К’,
в якій він нерухомий. Цей результат
називають сповільненням
часу.
.
Отже, годинники
у різних системах відліку йдуть
по-різному.
В системі К
відносно якої пристрій рухається,
годинник буде йти повільніше, ніж в
системі К’,
в якій він нерухомий. Цей результат
називають сповільненням
часу.
Час
![]() процесу в іншій системі відліку залежить
від швидкості руху
процесу в іншій системі відліку залежить
від швидкості руху
![]() цієї системи відносно іншої системи.
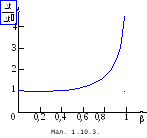
Ця залежність є суттєвою для швидкостей
цієї системи відносно іншої системи.
Ця залежність є суттєвою для швидкостей
![]() близьких до швидкості світла
близьких до швидкості світла
![]() (Мал. 1.10.3), а для
(Мал. 1.10.3), а для
![]() проміжки часу
проміжки часу
![]() .
Отже, на
відміну від класичної механіки плинність
часу залежить від стану руху.
Абсолютний рух класичної механіки
насправді є наближеним поняттям,
справедливим тільки при малих відносних
швидкостях. Релятивістське сповільнення
часу було підтверджено в явищі розпаду
мюонів, тим хто цікавиться - [7,с.144;9].
.
Отже, на
відміну від класичної механіки плинність
часу залежить від стану руху.
Абсолютний рух класичної механіки
насправді є наближеним поняттям,
справедливим тільки при малих відносних
швидкостях. Релятивістське сповільнення
часу було підтверджено в явищі розпаду
мюонів, тим хто цікавиться - [7,с.144;9].
Щодо відносності довжин відрізків, детально ви і самі можете вивчити це питання з [4-9]. Кінцева формула виглядатиме таким чином:
|
|
(1.10.8) |
О тже,
лінійний
розмір тіла в напрямі його руху
скорочується
в
тже,
лінійний
розмір тіла в напрямі його руху
скорочується
в
![]() раз і є меншим від його власної довжини
(
раз і є меншим від його власної довжини
(![]()
![]()
![]() )
Мал. 1.10.4. Цей результат називають
лоренцевим
скороченням.
Таким чином, на відміну від класичної
механіки, спеціальна теорія відносності
стверджує, що в різних інерціальних
системах відліку довжина стержня є
неоднаковою, вона залежить від стану
руху. Довжина
– величина відносна.
При малих швидкостях (
)
Мал. 1.10.4. Цей результат називають
лоренцевим
скороченням.
Таким чином, на відміну від класичної
механіки, спеціальна теорія відносності
стверджує, що в різних інерціальних
системах відліку довжина стержня є
неоднаковою, вона залежить від стану
руху. Довжина
– величина відносна.
При малих швидкостях (![]() )
)
![]() .
Лоренцеве скорочення довжини має суто
кінематичний характер
– в тілі не виникають напруження, які
б зумовили деформацію.
.
Лоренцеве скорочення довжини має суто
кінематичний характер
– в тілі не виникають напруження, які
б зумовили деформацію.
Зверніть увагу, що сповільнення часу і лоренцевське скорочення довжини – це реальні і об’єктивні факти. На запитання, які причини зумовлюють скорочення довжини і сповільнення часу, спеціальна теорія відносності відповідає, що жодних причин, якщо під цим розуміти певні фізичні процеси, які впливають на простір і час, не існує.
Відносність одночасності просторово розділених подій у різних інерціальних системах відліку, а також відносність довжин і проміжків часу в них, несумісні з перетвореннями Галілея. Щоб уникнути цієї несумісності, Ейнштейн замість перетворень Галілея, вив перетворення Лоренца.
Класичні
перетворення координат Галілея (1.10.2,
1.10.4) для двох інерціальних систем, що
рухаються так як на Мал. 1.10.1, але з
відносною швидкістю
![]() близькою до швидкості світла (
близькою до швидкості світла (![]() ),
і є більш загальними перетвореннями
Лоренца:
),
і є більш загальними перетвореннями
Лоренца:
|
|
(1.10.9) |
|
|
(1.10.10) |
Зауважимо декілька суттєвих обставин:
-
При

 ,
видно, що
,
видно, що
 і рівняння Лоренца (1.10.9-10) переходять
у рівняння Галілея (1.10.1-2). Отже, рівняння
Галілея не є абсолютно непридатними:
вони лише є наближеними. Причому точність
класичних рівнянь (1.10.1-1.10.4) тим вища,
чим меншою є відносна швидкість
і рівняння Лоренца (1.10.9-10) переходять
у рівняння Галілея (1.10.1-2). Отже, рівняння
Галілея не є абсолютно непридатними:
вони лише є наближеними. Причому точність
класичних рівнянь (1.10.1-1.10.4) тим вища,
чим меншою є відносна швидкість
 .
Інакше кажучи, при малих відносно
швидкості світла у вакуумі відносних
швидкостях руху класичні закони Галілея
є наближеними, але втім досить точними.
.
Інакше кажучи, при малих відносно
швидкості світла у вакуумі відносних
швидкостях руху класичні закони Галілея
є наближеними, але втім досить точними. -
Другий постулат Ейнштейна є несумісним з постулатом Галілея щодо однакового плину часу в різних системах відліку: якщо
 ,
то
,
то
 ,
як це видно з перетворень Лоренца.
Отже, час плине по різному в системах
К
та К’.
В цьому ви вже переконалися.
,
як це видно з перетворень Лоренца.
Отже, час плине по різному в системах
К
та К’.
В цьому ви вже переконалися. -
Взагалі при переході від системи К до системи К’ не зберігається ані інтервал часу (
 ),
ані інтервал довжини (
),
ані інтервал довжини ( ).
Проте зберігається деяка їх комбінація:
).
Проте зберігається деяка їх комбінація:
|
|
(1.10.11) |
Нарешті, закон складання швидкостей в релятивістській механіці (тобто механіці теорії відносності) виглядає складніше ніж вираз (1.10.4):
|
|
(1.10.12) |
Припустимо,
що, як було у дослідах Майкельсона,
![]() .
Тоді
.
Тоді
![]() - це швидкість руху Землі по орбіті
навколо Сонця. Підставимо
- це швидкість руху Землі по орбіті
навколо Сонця. Підставимо
![]() у формулу (1.10.12):
у формулу (1.10.12):
 .
Красивий і, можливо, дещо неочікуваний
результат, однак він повністю відповідає
другому постулату Ейнштейна та дослідам
Майкельсона.
.
Красивий і, можливо, дещо неочікуваний
результат, однак він повністю відповідає
другому постулату Ейнштейна та дослідам
Майкельсона.
Отже,
швидкість світла у вакуумі
![]() є максимально можливою швидкістю
передачі сигналів, перенесення взаємодій,
енергії в природі. Формули (1.10.12) виражає
релятивістський закон перетворення
швидкостей.
є максимально можливою швидкістю
передачі сигналів, перенесення взаємодій,
енергії в природі. Формули (1.10.12) виражає
релятивістський закон перетворення
швидкостей.
Чисельні експериментальні підтвердження перетворень Лоренца та постулатів Ейнштейна описані в [9,с.108-116].




 ,
або
,
або