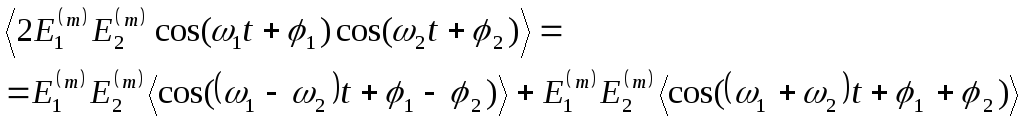|
Херсонський державний технічний університет Кафедра загальної та прикладної фізики |
КОЛИВАННЯ ТА ХВИЛІ Лекція 4.5. Інтерференція та дифракція світла |
|
|
|
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.5.
СВІТЛО. ІНТЕРФЕРЕНЦІЯ СВІТЛА-
Когерентність хвиль. Взаємодія двох когерентних хвиль
Припустимо,
що у деяку точку одночасно приходять
дві електромагнітні хвилі від двох
незалежних джерел. Хай напруженості
відповідних електричних полів у точці
спостереження дорівнюють
.
Згідно із принципом суперпозиції
напруженість результуючого електричного
поля двох ЕМХ повинна визначатися як
їх векторна сума:
|
|
(4.5.1) |
З
причин дуже високої частоти
оптичних коливань безпосередньо виміряти
напруженість електричного поля
електромагнітної хвилі у точці
спостереження важко. Всі приймачі
(сенсори) оптичного діапазону випромінювання
реагують, тобто вимірюють, середні за
певний проміжок часу
,
який визначається інерційністю сенсора,
енергетичні величини, пропорційні до
квадратів напруженості. Причому звичайно
.
Отже, експериментальні виміри пропорційні
середньому квадрату величини (4.5.1):
|
|
(4.5.2) |
Скалярний
добуток напруженостей
дорівнює нулю, якщо хвилі, які складаються
у точці спостереження, мають ортогональні
вектори напруженостей електричних
полів. Інакше кажучи, якщо обидві
хвилі є поляризованими у взаємно
перпендикулярних напрямах.
В такому разі, враховуючи, що інтенсивність
хвилі пропорційна квадрату її амплітуди
(
~
),
маємо з умови
:
|
|
(4.5.3) |
Інтенсивності неузгоджених поміж собою за напрямом поляризації (некогерентних) хвиль просто складаються у точці спостереження.
Припустимо,
що поляризація обох хвиль узгоджена,
однакова, коливання векторів
,
відбуваються уздовж одного напряму. Чи
досить цієї умови, аби третій фактор у
(4.5.2) не обертався в нуль? Дійсно, знайдемо
середнє значення добутку цих величин
(при однаковому напрямі, очевидно, можна
знаходити просто добуток їх модулів):
|
|
(4.5.4) |
Де зроблені наступні позначення:
|
|
(4.5.5) |
Причому
тут
-
радіус вектор точки спостереження,
- хвильові вектори обох хвиль,
- початкові фази.
Обидві
складові обертаються в нуль, оскільки
середні значення від періодичних функцій
за час значно більший від їх періоду
дорівнює нулю. Саме такий випадок
ми і маємо. Отже, якщо хвилі неузгоджені
за частотами
,
третій фактор у правій частині рівняння
також обертається в нуль і ми повертаємось
до умови – інтенсивності взаємодіючих
некогерентних хвиль арифметично
складаються у будь-якій точці.
Виключенням
є випадок
,
однакових частот взаємодіючих хвиль.
Хвилі
узгоджені за напрямами поляризації та
однакові за частотою в оптиці називають
когерентними (узгодженими).
Взаємодія двох (або взагалі обмеженого
числа, декількох) таких когерентних
хвиль має назву інтерференції.
Інтерференція, зрозуміло, відсутня для
некогерентних хвиль.
-
Інтерференційний фактор. Явище інтерференції
Розглянемо закон складання інтенсивностей для двох когерентних хвиль. З виразу (4.5.2) та (4.5.4) отримуємо:
|
|
(4.5.6) |
Третій фактор у рівнянні (4.5.6) називатимемо інтерференційним фактором. Він дорівнює нулю для некогерентних хвиль, як це з’ясовано у попередньому параграфі. Для когерентних хвиль різниця фаз поміж хвилями
|
|
(4.5.7) |
не залежить від часу, тому середнє значення косинуса у (4.5.6) просто дорівнює самій функції:
|
|
(4.5.8) |
де
.
Як
видно з останнього виразу інтерференційний
доданок до суми інтенсивностей у (4.5.8)
залежить від
- положення точки спостереження. Отже,
сумарна інтенсивність також повинна
змінюватися від точки до точки, значить,
вона є неоднорідною в просторі.
Поверхні рівної інтенсивності відповідають умові:
|
|
(4.5.9) |
і
є просто площинами, які перпендикулярні
вектору
.
Інтенсивність
максимальна там, де косинус у рівнянні
(4.5.8) приймає значення
,
причому
|
|
(4.5.10) |
і
більша за суму інтенсивностей.
Інтенсивність мінімальна там, де косинус
приймає значення
,
причому
|
|
(4.5.11) |
що менше суми інтенсивностей.
Таким
чином, під час складання (інтерференції)
двох когерентних хвиль інтенсивність
хвиль неоднорідно перерозподіляється
в просторі з утворенням максимумів та
мінімумів інтенсивності. Тоді як під
час складання некогерентних хвиль їх
інтенсивності однорідно складаються
в просторі і всюди сумарна інтенсивність
є простою сумою двох інтенсивностей.
Перерозподіл енергії когерентних
світлових хвиль в просторі та яскраво
виражена неоднорідність такого розподілу
і є головною ознакою явища інтерференції.
Особливо прозорим це твердження стає,
якщо розглянути випадок
.
За такої умови інтенсивність у максимумі
у чотири рази більша від інтенсивності
кожної хвилі, тоді як інтенсивність у
мінімумі взагалі стає нульовою, як це
видно з виразів (4.5.10-11).