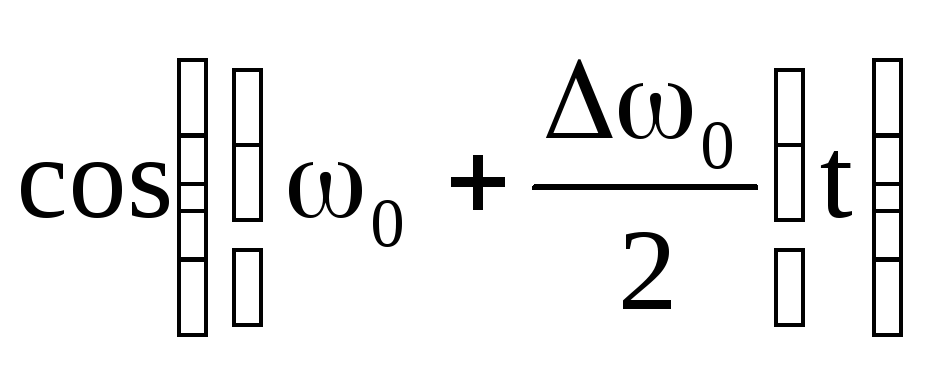Херсонський державний технічний університет Кафедра загальної та прикладної фізики

ХВИЛЬОВА ТА КВАНТОВА ОПТИКА Лекція 4.3. Механічні хвилі

	4.3. МЕХАНІЧНІ ХВИЛІ
	Складання двох незалежних гармонічних коливань однакового напрямку та однакової частоти
	Складання двох незалежних гармонічних коливань однакового напрямку та різної частоти
	Модульовані коливання
	Складання двох незалежних взаємно перпендикулярних гармонічних коливань. Фігури Лісажу*
	Пружні хвилі та їх характеристики
	Рівняння хвилі
	Хвилі в різних середовищах*
	Енергія пружної хвилі
	Стоячі хвилі. Вузли та пучності*
Елементи акустики*

• Складання коливань

У явіть собі матеріальну точку, на яку одночасно діє декілька різних пружних та квазіупружних сил. Кожна з цих сил спонукає точку здійснювати гармонічний коливальний рух. При спільній дії цих сил точка одночасно приймає участь у декількох незалежних рухах (спробуйте уявити хоча б траєкторію руху такої точки). З подібними прикладами додавання гармонічних коливань ми розберемося на наступних лекціях при розгляді принципу суперпозиції та інтерференції хвиль. Так, різні звукові хвилі, які одночасно сприймає ваше вухо, змушують барабанну перетинку приймати участь одразу в декількох гармонічних коливаннях. Електромагнітні хвилі, які одночасно приходять від радіостанцій, збуджують у приймаючому контурі електричні коливання різних частот.

К оливання можуть складатися і при цьому підсилювати, або гасити одне іншого, або результуючий рух може навіть не бути коливанням взагалі. Результат складання двох гармонічних коливань відчутне залежить від того які саме коливання складаються: однаково спрямовані, чи різноспрямовані. Ми розглянемо спершу складання коливань, які відбуваються незалежно один від одного, але в одному і тому ж напрямі. Помітимо, що коливання пари пов’язаних осциляторів, показаних на рис. 1 хоча і відбуваються в одному напрямі, проте взаємно незалежними не є. Отак, при додаванні двох гармонічних коливань одного напрямку виникає більш складний (ніж просто гармонічний) рух. З деякими прикладами ми ознайомимося. Для полегшення вирішення цієї задачі часто використовують графічне зображення коливань у вигляді векторів, що обертаються на площині. Отримані таким способом схеми називатимемо векторними діаграмами.

Розглянемо складання двох незалежних гармонічних коливань однакового напрямку та однакової частоти, рівняння яких є:

	(4.3.1а)
	(4.3.1б)

Зобразимо на векторній діаграмі обидва коливання як проекції двох векторів (довжиною відповідно та ), які обертаються з кутовою швидкістю , на координатну вісь (рис. 2). Через те, що кутові швидкості обертання однакові для двох векторів (тому що частота гармонічних коливань, що складаються, однакова), то результуюче коливання, яке зображується сумою векторів (=+), також є гармонічним, причому з тою ж самою частотою - . Амплітуда результуючого гармонічного коливання знаходиться за відомою з математики теоремою косинусів:

=

(4.3.2а)

Або в іншому, більш зручному для нас вигляді:

=

(4.3.2б)

З векторної діаграми видно, що результуюче коливання відбувається із частотою . Причому воно випереджає за фазою перше з коливань і відстає від фази другого.

Припустимо, що коливання, які ми складаємо мають різні частоти (), хоча й однаковий напрямок, тоді вектори на діаграмі рис. 3 обертаються з різною кутовою швидкістю (подібно хвилинній та годинній стрілкам годинника). Результуючий вектор пульсує за величиною і обертається з непостійною швидкістю за таких умов. Отже, результуюче коливання в цьому випадку не є гармонічним.

Якщо ж, наприклад, амплітуди коливань, що додаються, рівні, (початкові фази приймемо рівними нулю), а їх частоти не надто сильно відрізняються одна від одної , то вираз для опису коливань подібної системи осциляторів буде мати наступний вигляд:

=

А результат подібних коливань можна трактувати як коливання із амплітудою, яка повільно змінюється із постійною частотою (але зверніть увагу, такі коливання – негармонічні!). Вигляд подібних коливань показаний на рис. 4.

Я к видно, результуючий процес (сума двох гармонічних коливань різної частоти) не є гармонічним коливанням. Амплітуда коливань також не зберігається в часі. Такі періодичні, але негармонічні процеси називаються биттями [5-8]. При складанні подібних звукових коливань чутно буде звук певної висоти (частоти) із періодично змінюваною гучністю (амплітудою). Явищем биття користуються настроювачі музикальних інструментів. По зникненню биттів вони судять про точний збіг частоти струни та еталонного джерела звука. Явище (складання коливань близьких за частотою) також використовується у радіоприймачах – гетеродинах, які, в свою чергу використовуються у радіолокаторах [7, с.279].

Розглянемо також коливальні процеси, в яких за гармонічним законом змінюється або амплітуда коливань, або їх частота. Такі коливання називають модульованими коливаннями. Нехай амплітуда коливань з частотою (несуча частота) сама змінюється за гармонічним законом з частотою (частота модуляції). Отже рівняння амплітудно-модульованих коливань (АМ-коливань) матиме вигляд:

=

(4.3.3)

Відношення називають коефіцієнтом, або глибиною модуляції. Вигляд амплітудно модульованих коливань зображений на рис. 5. Амплітудна модуляція уживається тоді, коли треба передавати низькочастотний сигнал (), припустимо звукові частоти, використовуючи як носії сигналу високочастотні хвилі (), наприклад радіохвилі.

Можна, з тою ж метою, і також періодично, з частотою змінювати частоту коливань. Такий спосіб модуляції коливань має назву частотної модуляції (FM-модуляція). Отже, припустимо, що частота змінюється за гармонічним законом:

(4.3.4)

Тоді рівняння частотно-модульованих коливань виглядатиме так:

(4.3.5)

Вигляд частотно-модульованих (FM) коливань зображений на рис. 6. Амплітуда коливань в цьому випадку не змінюється, проте помітно змінюється частота. Варто зауважити, що модульовані коливання не є гармонічними коливаннями, як це видно з рис. 4, 5, 6. Отже, результатом складання декількох гармонічних коливань різної частоти (амплітуди)буде періодичний, але не гармонічний процес.

Д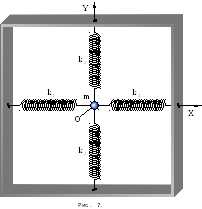 алі розглянемо випадки, коли складаються два гармонічних коливання, спрямовані у двох взаємно перпендикулярних напрямах.

В якості простої моделі такого тіла, яке коливається у двох взаємно перпендикулярних напрямах розглянемо матеріальну точку маси на чотирьох пружинах, як показано на рис. 7. Аналогічно моделі пружинного маятника поводитиме себе також електронний промінь осцилографа, якщо на вертикальну та горизонтальну пари пластин подати напруги різної амплітуди, що гармонічно змінюються в часі.

Матеріальна точка одночасно здійснює два гармонічні коливання - уздовж осі , та уздовж осі :

=	(4.3.6)
=	(4.3.7)

причому частоти цих коливань не обов’язково однакові.

В такому випадку траєкторія руху матеріальної точки може бути доволі складною. Проаналізуємо найпростішу умову: , тобто випадок, коли частоти коливань точно співпадають.

Припустимо спершу, що . Тоді рівняння (4.3.6) та (4.3.7) можна переписати у вигляді:

=, ==

(4.3.8)

Підносячи обидві частини рівнянь (4.3.8) у квадрат, отримуємо наступне рівняння траєкторії:

(4.3.9)

Яке очевидно, є канонічним рівнянням еліпсу з напівосями , . В залежності від різниці поміж початковими фазами коливань траєкторія може набувати виглядів, показаних на рис.8. Зокрема при еліптична траєкторія вироджується в відрізок прямої лінії – діагональ прямокутника зі сторонами ,. При матеріальна точка обертається за годинниковою стрілкою, при - відповідно проти годинникової стрілки. Отже, еліптичний (і зокрема також і коловий) рух можна розглядати як результат складання двох коливань однакової частоти, які здійснюються у взаємно перпендикулярних напрямах і мають певну різницю початкових фаз. Якщо частоти коливань не співпадають, але вони є кратними, тобто:

(4.3.10)

причому числа обов’язково є цілими числами, то траєкторія руху матеріальної точки являє собою так звані фігури Лісажу, показані на рис. 9, для різних сполучень (на рисункові ці числа позначені як ). ДО того ж співвідношення чисел дорівнює кількості дотикань траєкторії до сторін прямокутника, в який вона вписана. Траєкторії є замкненими, лише тоді, коли виконується співвідношення (4.3.10), тобто спостерігається кратність частот. Якщо частоти коливань не є кратними, і (4.3.10) не виконується, то траєкторія руху матеріальної частинки є незамкненою і поступово заповнює весь прямокутник зі сторонами як нитка з оберемка. Отже, всі складні періодичні рухи можуть бути представлені у вигляді суми гармонічних коливань різних напрямків, частот, амплітуд і початкових фаз.

Отже, із складання гармонічних коливань різних частот і напрямів результуючий рух осцилятора найчастіше являє собою складний коливальний процес. Можна представляти кожний складний коливальний процес як суму простих гармонічних коливань. У математиці, навіть, є доведене твердження, що будь-яку періодичну функцію =() з періодом можна подати як суму гармонічних функцій кратних частот, який має назву ряду Фур’є:

=+++...+++...

(4.3.11)

Практично гармонічний аналіз складного коливального процесу можна провести за допомогою набору резонаторів з різною власною частотою. Таким є, наприклад, язичковий частотомір [6, с. 184]. Він являє собою набір пружних язичків різної довжини прикріплених до пластини. Пластина зв’язується з досліджуваною коливальною системою. За умови збігу частот окремі язички реагують на прості коливання, що входять до складного коливального процесу.

В акустиці для аналізу складних звуків використовують набір резонаторів Гельмгольца - порожнистих куль різних розмірів з двома отворами: один для входу звуку, другий для сполучення з каналом вуха [6, с. 184]. Власну частоту коливань резонаторів Гельмгольца визначають так:

=

(4.3.12)

де - швидкість звуку, - площа вхідного отвору, - довжина вхідної шийки, - об’єм порожнини резонатора. Добираючи ті резонатори, які реагують на комплексний звук, можна дізнатися, з яких простих звуків він складається.