Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Херсонский национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методичн_ рекомендац_ї (МБ __ курс)

.pdf

Скачиваний:

Добавлен:

07.02.2016

Размер:

967.89 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

6. Дифракція світла на одній щілині
Умова мінімумів інтенсивності світла:
		a sinϕ = ±2k λ = ±kλ							(3.9)
				2
де a – ширина щілини, ϕ – кут дифракції, k =1, 2, 3, K – номер мінімуму.
Умова максимумів інтенсивності світла:
		a sinϕ = (2k +1)λ							(3.10)
7.	Дифракційна решітка			2
7.	Дифракційна решітка
Умова головних максимумів інтенсивності:
		d sinϕ = ±kλ							(3.11)
де	k = 0, 1, 2, 3, K – номер головного максимуму, d =				1	=	l	.–	період дифракційної
де	k = 0, 1, 2, 3, K – номер головного максимуму, d =					=	N	.–	період дифракційної
					N0		N
решітки,		N0 – кількість щілин на одиницю довжини решітки,					l	–	ширина дифракційної
решітки,		N – загальна кількість щілин.
Роздільна сила:			λ
		R =	λ	= kN					(3.12)
де		R =	λ	= kN					(3.12)
			λ
	λ – найменша різниця довжин хвиль двох сусідніх спектральних ліній ( λ і λ + λ ), при
якій ці лінії можна бачити роздільно у спектрі.
Кутова дисперсія:				k
		D =		k					(3.13)
		D =	d cosϕ						(3.13)
8.	Формула Вульфа-Брегга		d cosϕ
8.	Формула Вульфа-Брегга
		2c sinθ = kλ							(3.14)

де с – відстань між атомними площинами кристалу, θ – кут між напрямом рентгенівських променів, що падають на кристал і граню кристалу.

9. Поляризація світла
Закон Брюстера:
tgiB =	n2	= n21	(3.15)

	n1
де iB – кут падіння, при якому відбита світлова хвиля є повністю поляризованою,			n21 = n2 / n1
– відносний показник заломлення другого середовища відносно першого.
Закон Малюса:
I = I0 cos2 α			(3.16)

де І – інтенсивність плоскополяризованого світла, яке пройшло крізь аналізатор, І0 – інтенсивність плоскополяризованого світла, яке падає на аналізатор, α – кут між напрямом коливань світлового вектору хвилі, яка падає на аналізатор і площиною пропускання

аналізатора.

Ступінь поляризації при заломленні та відбиванні світла:

I − I||

sin(α −

β) 2

tg(α − β)

P =

; I

(3.17)

I + I||

sin(α +

β)

tg(α + β)

де I , I|| – – інтенсивності світла з коливаннями,

які є відповідно перпендикулярними і

паралельними до площини падіння,

– інтенсивність падаючого світла, α – кут падіння, β –

кут заломлення.

Кут повороту площини поляризації для розчину:

]Cl

ϕ = [α

(3.18)

4 n2 −sin 2 α

7λ

де [α] – питоме обертання, С – масова концентрація оптично активної речовини у розчині, l

– шлях світла у оптично активній речовині.

Приклади розв’язування задач

Приклад № 1

У просвітленій оптиці для усунення відбивання світла на поверхню лінзи наносять тонку плівку речовини з показником заломлення 1,26, який є меншим, аніж показник заломлення скла. При якій товщині плівки відбивання світла від лінзи не буде спостерігатися? Довжина хвилі падаючого світла 0,55 мкм, кут падіння 30°.

n = 1,26	Світло, падаючи на систему плівка-скло
λ = 5,5 10-7 м	під кутом α, відбивається як від верхньої
α = 30°	І, так й від нижньої ІІ поверхні плівки
h – ?	(рис.3.2,	n1 < n < n2 ,	n1 , n2 – показники
заломлення відповідно повітря і скла). Промені S1 i S2 є
когерентними, оскільки утворюються з одного променя S.
Результат інтерференції цих променів залежить від
оптичної різниці ходу.		Промені	відбиваються від	Рис. 3.2.

середовища з більшим показником заломлення, тому як на верхній, так й на нижній поверхні плівки відбувається втрата на півхвилі і тому фаза

коливань обох променів S1 i S2 змінюється однаково. Отже, результат інтерференції цих променів буде такий самий, як би ніякого зміни фази не було, тобто оптична різниця ходу хвиль дорівнює

= 2h n2 −sin 2 α

(1)

Як відомо, умова максимального ослаблення світла при інтерференції у тонких плівках полягає у тому, що оптична різниця інтерферуючих хвиль повинна дорівнювати непарному числу на півхвиль:

= (2k +1)λ2

де k = 0, 1, 2, 3, K – порядок інтерференційного мінімуму. З (1) і (2) слідує

2h n2	−sin 2 α = (2k +1)λ
Звідки для товщини плівки маємо:		2
Звідки для товщини плівки маємо:		(2k +1)λ
hk	=	(2k +1)λ
[hk ]= [λ]= м	4	n2 −sin 2 α
[hk ]= [λ]= м

Покладаючи k = 0, 1, 2, 3, K, отримаємо ряд значень товщини плівки:

h0	=		λ	= 0,12 мкм
		n2	−sin 2 α
	4
h1	=		3λ	= 3h0	= 0,36	мкм
		n2	−sin 2 α
	4
h2	=		5λ	= 5h0	= 0,60	мкм

(2)

(3)

(4)

h3 = = 7h0 = 0,84 мкм

Відповідь: h = 0,12; 0,36; 0,60; 0,84; ...(мкм)

Приклад № 2

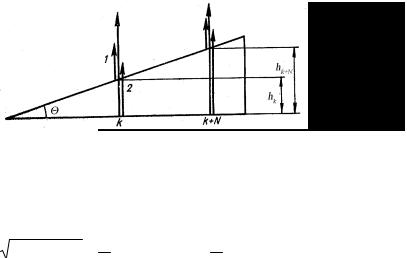
На скляний клин нормально до його грані падає монохроматичне світло з довжиною хвилі 0,66 мкм. Число темних інтерференційних смуг на 1 см дорівнює 10. Визначити заломлюючий кут клину. Спостереження проводять у відбитому світлі.

λ = 6,6 10-7 м	Паралельний	пучок	проме-
l = 0,01 м	нів, відбиваючись від верх-
N = 10	ньої і нижньої граней клину,
n = 1,6	інтерферують,	утворюючи
θ – ?	стійку картину. Так як інтер-
	ференція на клині спосте-
рігається при	малих заломлюючих		кутах	Рис. 3.3.

клину, промені, які відбиваються від верхньої та нижньої граней, можна вважати паралельними (промені 1 і 2 на рис. 3.3). Оскільки

спостереження проводять у відбитому світлі і на верхній та нижній гранях відбувається відбивання від більш оптично густого середовища (показник заломлення скла більший за показник заломлення повітря), то для оптичної різниці ходу променів 1 і 2 можемо записати:

= 2h n2 −sin 2	α + λ =	2h n cos β + λ		(1)
k	2	k	2
Умова інтерференційного мінімуму має вид:	2		2
Умова інтерференційного мінімуму має вид:	(2k +1)λ
=	(2k +1)λ			(2)
Прирівнюємо праві частини рівнянь (1) і (2):	2
Прирівнюємо праві частини рівнянь (1) і (2):
2h n cos β + λ = (2k +1)λ				(3)
k	2	2
	2	2
Враховуючи, що кут падіння α = 0 , а cos β =1, можемо записати
2hk n = kλ				(4)

Нехай темній смузі з номером k відповідає товщина hk , а смузі з номером k + N відповідає товщина hk +N . Для hk і hk +N з рівняння (4) можемо записати

kλ

;

(k + N )λ

(5)

k +N

Згідно умови задачі на відстані l вкладається N

інтерференційних смуг. З рис.3.3 очевидно,

що

hk +N − hk

sinθ =

(6)

Оскільки кут θ дуже малий, можна покласти sinθ ≈θ

і тоді остаточно маємо

k + N

λ −

hk +N − hk

Nλ

θ =

(7)

2nl

Відповідь: θ = 2,2 10-4 рад.

Приклад № 3

Установка для спостереження кілець Ньютона опромінюється монохроматичним світлом, яке падає нормально. Відстань між світлими кільцями з номерами k1 і k2 дорівнює l . Радіус

викривлення лінзи R .

Знайти довжину світлової хвилі. Спостереження проводять у відбитому світлі. Установку розміщено у середовищі з показником заломлення n .

k1 k2 l

R n

λ – ?

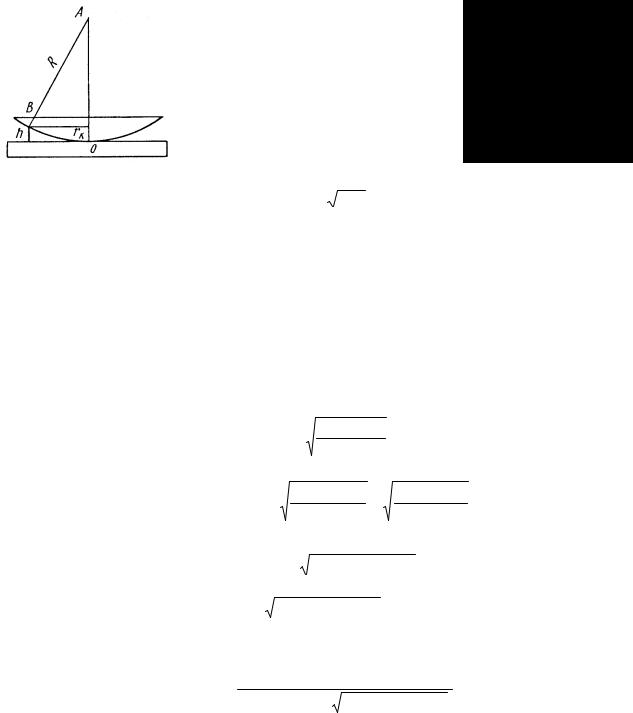
Виразимо радіус кільця rk через радіус

викривлення лінзи R і товщину h прошарку між скляною пластинкою і лінзою у місці спостереження даного кільця. Для цього скористаємось теоремою Піфагора (рис.3.4):

rk2 = R2 − (R − h)2 = R2 − R2 + 2Rh − h2 = 2Rh − h2

Оскільки товщина прошарку між скляною пластинкою і лінзою
дуже мала, можемо покласти її квадрат у першому наближенні	Рис. 3.4.
рівним нулеві h2 ≈ 0 . Тоді остаточно для радіусу rk маємо	Рис. 3.4.
rk = 2Rh	(1)

Умова інтерференційного максимуму полягає у тому, що на оптичній різниці ходу двох променів повинна укладатися ціле число довжин хвиль:

= kλ 2hn cos β + λ

= kλ

(2)

Виразимо з рівняння (2) товщину прошарку

kλ −

λ(2k −1)

h =

(3)

2n cos β

Тут ураховано, що при нормальному падінні променів β = 0, cos β =1.

Підстановка (3) у (1) дає радіус світлого кільця у відбитому світлі:

(2k −1)Rλ

(4)

Далі, для відомої відстані між кільцями можемо записати

l = rk

− rk =

(2k2 −1)Rλ

−

(2k1 −1)Rλ

(5)

Піднесемо обидві частини рівняння (5) до квадрату і зробимо можливі спрощення:

l 2 =

(2k2 −1)Rλ

− 2

Rλ

(2k2 −1)(2k1

−1)+ (2k1 −1)Rλ

=	Rλ	(k2 + k1 −1− (2k2 −1)(2k1 −1))

	n

Звідси легко отримати кінцевий вираз для довжини хвилі, який й буде остаточною відповіддю задачі, оскільки вона сформульована у загальному вигляді.

		λ =	nl 2	(6)
[λ]=	м2		R(k2 + k1 −1 − (2k2 −1)(2k1 −1))
		= м
	м

Приклад № 4

На дифракційну решітку Д нормально падає монохроматичне світло з довжиною хвилі 0,55 мкм. На екрані Е, який розташовано паралельно решітці на відстані 0,5 м від неї, спостерігається дифракційна картина (рис.3.5). Відстань між дифракційними максимумами першого порядку дорівнює 10,2 см. Визначити сталу дифракційної решітки, число штрихів на 1 см, максимальний порядок спектру, загальне число головних максимумів, максимальний кут відхилення променів, який відповідає останньому дифракційному максимуму.

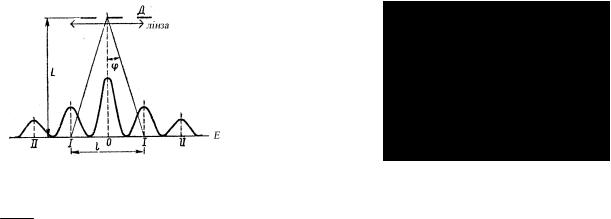
λ = 5,5 10-7 м	Запишемо умову	головних максимумів
L = 0,5 м	дифракційної решітки:
l = 0,12 м		d sinϕ = kλ			(1)
k = 1	Враховуючи той	факт, що l / 2 << L
d – ?	(рис.3.5), маємо
N0 – ?	sinϕ ≈ tgϕ =		l		(2)
kmax – ?
			2L

n – ?
n – ?	Підставляючи (2) у (1), отримаємо
ϕmax – ?	Підставляючи (2) у (1), отримаємо
				dl	= kλ d =	2λL	Рис. 3.5.
				dl		2λL	Рис. 3.5.
							(3)
				2L		l	(3)

[d ]= ммм = м; d = 4,6 10-6м = 4,6 мкм.

Число штрихів на 1 см довжини дифракційної решітки легко розрахувати через сталу решітки:

		d =	1	N0	=	1	(4)
		d =	N0	N0	=	d	(4)
			N0			d
При розрахунках за формулою (4) сталу дифракційної решітки d треба підставляти у см.
[N0 ]=	1	; N0 = 2,2 103 см-1.
[N0 ]=	см	; N0 = 2,2 103 см-1.
	см

Для визначення загального числа головних максимумів, що їх дає дифракційна решітка, виходимо з умови, що максимальний кут відхилення променів від нормального

розповсюдження не може перевищувати 90°, тобто				sin 90o =1 . Тоді формула (1)		набуває
вигляду:					d
d = k	max	λ k	max	=		(5)
					λ

kmax = 8,3 = 8.

(Важливо! При визначенні максимального порядку дифракційного спектру решітки у випадку, коли отримаємо дробовий результат, завжди треба його заокруглювати до найменшого цілого, наприклад, якщо розрахунок дає 7,9, то маємо записати kmax = 7.)

Загальне число максимумів дорівнює

n = 2kmax +1

(6)

тобто вліво і вправо від центрального максимуму спостерігається по kmax максимумів. n = 17.

Для визначення максимального кута відхилення променів перепишемо рівняння (1) у вигляді:

k	max	λ
d sinϕmax = kmax λ ϕmax = arcsin			(7)
	d

ϕmax = 73,7o .

Відповідь: d = 4,6 10-6м = 4,6 мкм; N0 = 2,2 103 см-1; kmax = 8; n = 17; ϕmax = 73,7°.

Приклад № 5

На діафрагму з круглим отвором радіусом 1 мм падає нормально паралельний пучок світла з довжиною хвилі 0,5 мкм. На шляху променів, які пройшли отвір, розміщують екран. Визначити максимальну відстань від центру отвору до екрану, при якій у центрі дифракційної картини ще буде спостерігатися темна пляма.

ρ = 10-3 м	Відстань, при якій буде спостерігатися темна пляма, визначається числом
λ = 5 10-7 м	зон Френеля, що укладаються у отворі. Якщо число зон парне, то у центрі
bmax – ?	дифракційної картини буде темна пляма.

n1 = 1,31 n2 = 2,42

iB – ? P1 – ? P2 – ?

Рис. 3.7.

Рис. 3.6.

Число зон Френеля, які укладаються у отворі, убуває з віддаленням екрану від отвору. Найменше число зон дорівнює двом. Отже, максимальна відстань, при якій ще буде спостерігатися темна пляма у центрі екрану, визначається умовою, згідно з якою у отворі повинно розміститися дві зони Френеля.

1-й спосіб З рис.3.6 слідує, що відстань від точки спостереження О

на екрані до краю отвору на 2 λ2 більша за відстань

R0 = bmax .

За теоремою Піфагора отримаємо

−b

= 2λb + λ

(1)

= b

max

Враховуючи, що λ << b і що членом λ2

можна знехтувати,

перепишемо рівняння (1) у

max

вигляді:

ρ2 = 2λb

ρ2

(2)

max

2λ

2-й спосіб

Вважатимемо, що хвиля є плоскою. Тоді радіус k -й зони Френеля для плоскої хвилі:

ρ = bkλ

(3)

Ми з’ясували, що максимальній відстані bmax , при якій у центрі екрану буде спостерігатися темна пляма, відповідає k = 2 зони Френеля. Отже, рівняння (3) можна переписати у вигляді:

				ρ = 2λb	b =	ρ2	(4)
				max	max	2λ
						2λ
Як бачимо, це рівняння повністю співпадає з рівнянням (2).
[b		]=	м2	= м; b =1 м.
[b		]=	м	= м; b =1 м.
	max		м	max

Відповідь: bmax = 1 м.

Приклад № 6

Промінь світла, пройшовши крізь шар льоду, падає на алмазну пластинку, частково відбивається, частково заломлюється. Визначити, яким повинен бути кут падіння, щоб відбитий промінь був максимально поляризований. Знайти ступінь поляризації відбитого і заломленого світла.

Якщо кут падіння світла на межу розділу двох діелектриків не дорівнює нулю, відбитий і заломлений промені є частково поляризованими. У відбитому промені переважають коливання, що є перпендикулярні до площини падіння (на рис.3.7 ці коливання

позначені точками), у заломленому промені – коливання, що є паралельними до площини падіння (на рис.3.7 вони позначені

стрілками). Відбите світло є максимально поляризованим при куті падіння задовольняє закону Брюстера:

tgiB = n2 = n21 n

α = iB , який

(1)

Якщо α = iB , то відбитий та заломлений промені взаємно перпендикулярні, тобто

α + β = 90o (рис.3.7). Світло, яке пройшло, є		частково	поляризованим. З рівняння (1)
знаходимо
		n2
iB		n2	(2)

	= arctg n
		1

iB = 61,5°.

Для ступеня поляризації відбитого променя маємо:

I − I||

(3)

I + I||

sin(α − β)

tg(α − β)

де

; I

(4)

sin(α + β)

tg(α + β)

– інтенсивності світла з коливаннями, які є відповідно перпендикулярними і паралельними до площини падіння, α – кут падіння, β – кут заломлення.

Для відбитого променя з формул (4) отримаємо:

I =

sin 2 (iB − β);

I||

= 0

оскільки sin(iB + β)= sin 90o =1 ; tg900

→ ∞ .

Ступінь поляризації відбитого променя дорівнює

=1 =100% .

Знайдемо інтенсивності світла після заломлення:

I ' =

− I =

−

sin(iB − β)=

(1 −sin 2 (iB − β)); I||' =

Тоді ступінь поляризації заломленого променя дорівнює:

P2	=	I\|\|'	− I '	=		sin 2 (iB − β)
		I\|\|'	+ I '		2	−sin 2 (iB − β)

P2 = 0,17 =17% .

Відповідь: iB = 61,5°, Р1 = 100%, Р2 = 17%.

(5)

(6)

(7)

Задачі для самостійного розв’язання

1.Установка “Кільця Ньютона” опромінюється монохроматичним світлом з довжиною хвилі 0,6 мкм. Знайти товщину повітряного шару поміж лінзою та скляною пластиною у тому місці, де спостерігається п’яте темне кільце у відбитому світлі.

2.На дифракційну решітку нормально падає промінь світла від розрядної трубки, що наповнена гелієм. На яку лінію у спектрі третього порядку накладається червона лінія гелію (λ = 670 нм) спектру другого порядку?

3.На дифракційну решітку нормально падає монохроматичне світло. Період решітки дорівнює 2 мкм. Якого найбільшого порядку дифракційний максимум дає ця решітка у випадку червоного (λ1 = 0,7 мкм) і фіолетового (λ2 = 0,45 мкм) світла?

4.Знайти радіус викривлення лінзи, що застосовується для спостереження кілець Ньютона, якщо відстань поміж другим та третім світлими кільцями 0,5 мм. Установка опромінюється світлом з довжиною хвилі 5,5 10-7 м. Спостереження проводять у відбитому світлі.

5.На якій відстані від дифракційної решітки необхідно поставити екран, щоб відстань між нульовим максимумом і спектром четвертого порядку була рівною 50 мм для світла з довжиною хвилі 500 нм? Стала дифракційної решітки 0,02 мм.

6.Визначити кут дифракції для спектру другого порядку натрію з довжиною хвилі 589 нм, якщо на 1 мм дифракційної решітки припадає п’ять штрихів.

7.Визначити найбільший порядок спектру, який може створювати дифракційна решітка, що має 500 штрихів на 1 мм, якщо довжина падаючого світла 590 нм. Яку найбільшу довжину хвилі можна спостерігати у спектрі цієї решітки?

8.Кільця Ньютона утворюються поміж плоским склом і лінзою з радіусом викривлення 8,6 м. Монохроматичне світло падає нормально. Діаметр четвертого темного кільця дорівнює 9 мм. Знайти довжину хвилі падаючого світла. Спостереження проводять у відбитому світлі.

9.На дифракційну решітку, яка містить 400 штрихів на 1 мм, падає нормально монохроматичне світло (λ = 0,6 мкм). Знайти загальну кількість дифракційних максимумів, які дає ця решітка. Визначити кут ϕ дифракції, який відповідає останньому максимуму.

10.Відстань поміж другим та першим темними кільцями Ньютона у відбитому світлі дорівнює 1 мм. Визначити відстань поміж десятим та дев’ятим кільцями.

11.Промінь світла переходить із води (n1 = 1,33) в алмаз (n2 = 2,42). При цьому промінь, відбитий від межі розділу цих середовищ є максимально поляризований. Визначити кут між падаючим та заломленим променями.

12.На кристал алмазу (n2 = 2,42) падає пучок природного світла під кутом Брюстера. Визначити ступінь поляризації відбитого та заломленого світла.

13.На поверхню скла (n2 = 1,52) падає пучок природного світла під кутом 45°. Знайти ступінь поляризації відбитого світла.

14.Поміж скляною пластинкою і лінзою налито рідину. Радіус восьмого темного кільця Ньютона при спостереженні у відбитому світлі (λ = 700 нм) дорівнює 2 мм. Радіус викривлення лінзи дорівнює 1 м. Знайти показник заломлення рідини.

15.Дифракційна решітка опромінюється монохроматичним світлом. Максимум другого порядку відхиляється на кут 14°. На який кут відхиляється максимум третього порядку?

16.Обчислити радіус ρ5 п’ятої зони Френеля для плоского хвильового фронту (λ = 0,5 мкм), якщо точка спостереження знаходиться на відстані 1 м від фронту хвилі.

17.Радіус ρ4 четвертої зони Френеля для плоского хвильового фронту дорівнює 3 мм. Визначити радіус ρ6 шостої зони Френеля.

18.Пучок монохроматичних (λ = 0,6 мкм) хвиль у повітрі падає під кутом 30° на мильну плівку (n = 1,3). При якій найменшій товщині плівки відбиті світлові хвилі будуть максимально інтерференційно послаблені?

19.Пучок монохроматичних (λ = 0,6 мкм) хвиль у повітрі падає під кутом 30° на мильну плівку (n = 1,3). При якій найменшій товщині плівки відбиті світлові хвилі будуть максимально інтерференційно підсилені?

20.На тонкий скляний клин (n = 1,55) падає нормально монохроматичне світло. Кут у вершині клину 2’. Визначити довжину світлової хвилі, якщо відстань між сусідніми інтерференційними максимумами у відбитому світлі дорівнює 0,3 мм.

21.Кут Брюстера при падінні світла з повітря на кристал кам’яної солі дорівнює 57°. Визначити швидкість світла у цьому кристалі

22.На мильну плівку (n = 1,3) падає світло під кутом 45°. При якій найменшій товщині плівки відбити промені будуть жовтими (λ = 600 нм)?

23.На скляний клин нормально падає монохроматичне світло (λ = 0,55 мкм). Визначити ширину інтерференційної смуги. Кут у вершині клина 0,2’.

24.На скляний клин нормально падає монохроматичне світло (λ = 600 нм). Визначити кут у вершині клина, якщо відстань між сусідніми інтерференційними мінімумами у відбитому світлі дорівнює 4 мм.

25.У досліді „Кільця Ньютонв” визначити товщину шару повітря у тому місці, де у відбитому світлі (λ = 0,6 мкм) видно перше світле кільце.

26.Діаметри двох світлих кілець Ньютона відповідно дорівнюють 4,0 і 4,8 мм. Відомо, що між цими кільцями розташовано три світлих кільця. Кільця спостерігаються у відбитому світлі (λ = 500 нм). Знайти радіус викривлення лінзи.

27.На установці „Кільця Ньютона” був виміряний радіус третього темного кільця. Коли простір між скляною пластиною і лінзою заповнили рідиною, той самий радіус має четверте темне кільце. Визначити показник заломлення рідини.

28.За допомогою дифракційної решітки необхідно розділити дублет натрію (λ1 = 589 нм і λ2 = 589,6 нм) у спектрі другого порядку. При якій найменшій довжині решітки це можливо?

29.Дифракційна решітка опромінюється монохроматичним світлом. У дифракційній картині

максимум другого порядку спостерігається під кутом ϕ1 = 14°. На який кут ϕ2 відхиляється максимум третього порядку?

30.Пучок світла, який розповсюджується у повітрі, падає на поверхню рідини під кутом 54°. Визначити кут заломлення пучка, якщо відбитий пучок є повністю поляризований.

Тема 4. Теплове випромінювання

З усього різноманіття електромагнітних випромінювань, які сприймаються або не сприймаються людським оком, можна виокремити одне, яке властиве усім тілам. Це випромінювання нагрітих тіл, або інакше теплове випромінювання. Воно виникає при будьяких температурах вище за абсолютний нуль, тому випромінюється усіма тілами. В залежності від температури тіла змінюються інтенсивність випромінювання і спектральний склад, тому далеко не завжди теплове випромінювання сприймається оком як світіння.

Методичні рекомендації

Перехід від класичної фізики до квантової пов’язаний з проблемою теплового випромінювання і, особливо, з питанням розподілу енергії у спектрі абсолютно чорного тіла (АЧТ). При розв’язанні задач даної теми слід чітко розуміти, що математичним підґрунтям законів теплового випромінювання є формула Планка. Але вигляд формули Планка залежить від спектральної шкали, якою користуються. Співставлення формул (4.1, 4.2), які дають спектральні густини випромінювальної здатності АЧТ за шкалою довжин хвиль і частот, показує, що ці функції мають різну розмірність і максимуми цих функцій при однаковій температурі не співпадають. Причому максимуми розходяться достатньо сильно: коли один з них лежить у видимій частині спектру, інший – у інфрачервоній. Але у цьому не має чогось дивного, адже спектральна густина випромінювання є лише допоміжна величина, на яку треба множити відрізок спектральної шкали, щоб отримати променевий потік. Положення максимуму спектральної кривої випромінювання само по собі фізичного змісту не має.

При розв’язанні задач на закон Віна слід працювати у одній спектральній шкалі (довжин хвиль або частот) і пам’ятати, що перехід від закону Віна по довжинах хвиль (4.5) до закону

Віна по частотах (4.6) за допомогою формули λmax = c / vmax' виконувати не можна, оскільки частота vmax' , розрахована в такій спосіб не буде співпадати з максимумом vmax по шкалі частот: vmax' ≠ vmax . Теж саме є справедливим стосовно довжин хвиль.

При використанні закону Стефана-Больцмана (4.3) треба пам’ятати, що він сформульований для абсолютно чорного тіла, і у випадку не чорного тіла слід вводити поправку у вигляді коефіцієнта чорності (4.4). Також не слід забувати, що температуру у закон Стефана-Больцмана треба підставляти за шкалою Кельвіна.

Фізична величина	Позначення	Одиниці вимірювання
		Вт/м2
Енергетична світність	R	Вт/м2
Стала Стефана-Больцмана	σ = 5,67 10-8	Вт/(м2 К4)
Стала Віна (шкала λ)	b = 2,9 10-3	м К
Стала Віна (шкала ω)	b1 = 3,69 1011	(с К)-1
Швидкість світла у вакуумі	с = 3 108	м/с
Спектральна густина	r	Дж/м	2
Спектральна густина	ω	Дж/м
випромінювальної здатності АЧТ	rλ	Дж/(с м3)
Потужність	N	Вт
Стала Планка	h = 6,63 10-34	Дж с
Стала Планка	h = h /(2π )=1,05 10−34	Дж с
Стала Больцмана	k0 = 1,38 10-38	Дж/К
Коефіцієнт чорності	аТ	—
Частота світла	v, ω	Гц
Довжина хвилі світла	λ	м
Абсолютна температура	Т	К

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>