Тема 15. Стійкість стиснених стержнів.

Лекція 26. Поняття про стійкість. Задача Ейлера. Критичні напруження. Межі придатності формули Ейлера. Практичний розрахунок стержнів на стійкість.

Задачу на знаходження величини критичної сили чи критичного навантаження для стержня вперше розв‘язав Ейлер. Це розв‘язання стосується того випадку, коли втрата стійкості відбувається у межах пружності. При цьому не має значення, чи діє сила строго по осі стержня, чи є початковий ексцентриситет або невелике викривлення.

Практичний розрахунок на стійкість проводиться як на звичайний стиск, проте із зменшеним допустимим напруженням. Це зменшення основного допустимого напруження визначається коефіцієнтом , меншим за одиницю, який залежить від матеріалу і гнучкості стержня.

Розглянемо основні типи задач, які розв‘язуються при розрахунках стержнів на стійкість.

Для стержня заданої довжини і відомого поперечного перерізу знайти величину критичної сили. Для цього спочатку визначаємо гнучкість стержня. Якщо вона більше 100 (для м’якої сталі), використовуємо для знаходження критичної сили формулу Ейлера

,

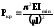де l – зведена довжина; - залежить від характеру закріплення кінців.

Формула Ейлера справедлива тільки в границях пружності – для стержнів великої гнучкості (приблизно для >100): .

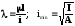Якщо гнучкість <100, для визначення P_кр використовуємо формулу Ясинського.

За заданою площею перерізу і довжиною знайти допустиме навантаження. Цю задачу можна розв‘язати як попередню. Спочатку знаходимо критичну силу і, задавшись запасом стійкості, знаходимо допустиме навантаження. Можна для розв‘язання цієї задачі скористатися таблицями коефіцієнтів . Спочатку знаходимо гнучкість стержня, потім за таблицями шукаємо коефіцієнт  і, помноживши його на основне допустиме напруження, знаходимо зменшене допустиме напруження, яке враховує стійкість. Помноживши цю останню величину на площу поперечного перерізу, знаходимо допустиме навантаження.

Підібрати переріз стиснутого стержня. Замість двох формул Ейлера і Ясинського, кожна з яких придатна для відповідних інтервалів гнучкостей, зручно мати одну формулу, котра придатна для будь-якої гнучкості стержня.

Ця практична формула має вигляд

,

де 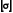– основне допустиме напруження;  - коефіцієнт зменшення основного допустимого напруження (0<<1); A - площа.

Щоб підібрати переріз, тут доводиться задаватися або площею, або коефіцієнтом ₀, а потім, підібравши площу, уточнити нове значення  і зіставити його з початковим ₀. Після кількох наближень можна добитись того, щоб наступне значення мало чим відрізнялось від попереднього значення , або, інакше кажучи, щоб справжнє напруження було близьким до допустимого при поздовжньому згині.

Лекція 27. Енергетичний метод визначення критичної сили. Динамічний метод визначення критичної сили.

1. Визначення величини критичної сили як функції переміщення стержня. Особливість цієї задачі полягає в тому, що при згинанні балки поперечні навантаження виконують роботу на прогинах, які є переміщеннями першого порядку малості. При поздовжньому навантаженні силою враховується робота цієї сили на переміщеннях другого порядку малості.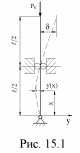

На основі енергетичних залежностей для двох станів: згинання балки від поперечного навантаження і згинання балки від поздовжнього навантаження – дістанемо такий вираз для критичної сили:

,

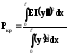де y - поперечний прогин, який є функцією від абсциси перерізу стержня.

Для визначення критичної сили енергетичним способом треба знайти рівняння зігнутої осі стержня, яке б задовольняло усім граничним умовам.

Енергетичний метод дає невелике відхилення від точного значення параметра критичної сили. Значення критичної сили, яке визначається за цим методом, дещо вище дійсного. Для підтвердження цього розглянемо визначення коефіцієнта приведеної довжини  для однопрольотного стояка з консольним і нижнім шарнірно обпертим кінцем (рис.15.1).

Для розв‘язання задачі вибираємо форму зігнутої осі стержня у вигляді такої алгебраїчної функції:

.

Коефіцієнти a₀, a₁, a₂, a₃, a₄ будемо підбирати так, щоб задовольнити граничні умови стояка:

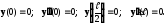
Із першої і другої граничних умов отримаємо a₀=0; a₂=0. Із третьої умови знайдемо

.

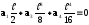Із четвертої умови знайдемо

.

Отже, для визначення коефіцієнтів a₁, a₃, a₄ маємо систему рівнянь:

;

.

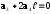Звідки отримаємо .

Тоді рівняння пружної лінії стержня набирає вигляду

.

Далі знаходимо:

;

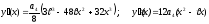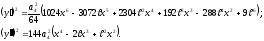
Інтеграли .

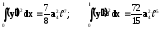Підставляючи знайдені значення інтегралів у формулу для критичної сили, дістанемо

.

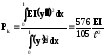Перепишемо цей вираз так:

,

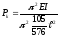тобто 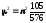, а шуканий коефіцієнт приведення довжини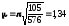. Значення для даного стояка, яке одержане за допомогою інтегрування диференціального рівняння його пружної лінії, дорівнює 1,35. Таким чином, відхилення наближеного розв‘язку від більш точного складає 0,6%.

2. Динамічний метод визначення критичної сили. Згідно з динамічним критерієм стійкості умовою переходу від стійкої форми рівноваги стержня до нестійкої є рівність нулеві частоти власних коливань стисненого стержня (перехід від дійсних значень до неявних).

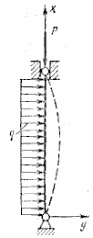
Рис. 15.2

Для складання рівняння власних коливань запишемо спочатку наближене диференціальне рівняння зігнутої осі стержня, стисненого силою Р і зігнутого поперечним навантаженням інтенсивності q (рис.15.2):

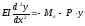, (1)

де М_п – згинаючий момент від поперечного навантаження.

Продиференціювавши (1) двічі по х, отримаємо

, (2)

де .

Враховуючи рівняння (2), можна отримати рівняння поперечних коливань стиснутого стержня, якщо розглядати переміщення у не тільки як функцію координати х, а також і як функцію часу t, а замість поперечного навантаження розуміти, згідно принципу Даламбера, сили інерції , (3)

де – μ одинична маса стержня.

Підставивши (3) в праву частину (2) і замінивши в лівій звичайні похідні на частинні, отримаємо рівняння власних коливань стисненого стержня у вигляді

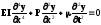. (4).

Розв’язок рівняння, застосовуючи метод Фур’є, шукаємо у вигляді

, (5)

де - невідома поки функція часу, ℓ - довжина стержня, а- визначає форму пружної лінії стержня при коливаннях.

Підставляючи вираз (5) у рівняння (4), матимемо

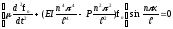(6)

Рівняння (6) буде виконуватися при будь-яких х, якщо 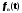буде задовольняти рівнянню

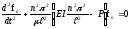. (7)

Позначимо

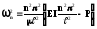. (8)

Тоді рівняння (7) перепишемо так:

. (9)

Тут 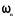- частота власних коливань стержня при згині поn півхвилях синусоїди. Розв’язок рівняння (9) має вигляд

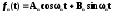. (10)

Отже, . (11)

Розглянемо вираз (8) для частоти 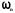. Якщо різниця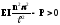для будь-якого значенняn, то вираз (11) буде характеризувати гармонічні коливання із амплітудами, які визначаються початковим збурюванням. Якщ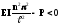о , то буденеявне число.

Отже, прямолінійна форма рівноваги стержня, стиснена силою Р, буде стійкою до тих пір, поки 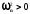, і буде нестійкою при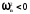; критерієм втрати стійкості розглядуваного стержня буде рівність нулеві власних коливань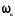хоча б для однієї форми коливань, що відповідає тонуn. Частота 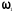(стержень коливається в основному тоні з однією півхвилею) дорівнює нулеві, коли сила Р досягає критичного значення:.

Лекція 28. Поздовжньо-поперечний згин.

Слід зазначити, що згин прямого бруса зветься поздовжньо-поперечним, якщо в його поперечних перерізах виникають згинаючі моменти як від поздовжніх, так і від поперечних навантажень (рис.15.3). При розрахунку згинаючі моменти М в поперечних перерізах обчислюють з урахуванням прогинів осі бруса:

, (1)

де М_П – згинаючий момент від поперечного навантаження.

Диференціальне рівняння зігнутої осі має вигляд

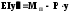. (2)

Рис. 15.3

При відсутності поздовжньої сили

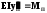. (3)

Тоді вираз (2) можна записати так:

. (4)

Нехай форма пружної лінії балки при наявності поздовжньої сили і без неї є синусоїда:

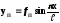;. (5)

Підставивши значення у та у_п з формул (5) у вираз (4), одержимо

,

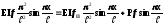звідки 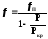де. (6)

У випадку розтягу 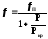. (7)

Максимальний згинаючий момент 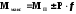. Найбільше нормальне напруження можна знайти

за формулою .

При поздовжньо-поперечному згині обчислення сумарного напруження ускладнюється тим, що в цьому разі принцип незалежності дії сил застосувати неможливо.

Розв’язання задач по темі “Стійкість стиснутих стержнів”.

Задача 15.1. Підібрати у вигляді двотавра поперечний переріз шарнірно опорного стержня завдовжки ℓ=4 м. Стержень стиснутий силами Р=300кН, [σ]=160 МПа.

Розв’язання. У першому наближенні вибираємо φ=0,6. Тоді

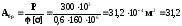см².

За таблицями для двотавра №20а маємо А=35,5 см², і_min=2,12 см. Отже

.

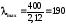За таблицею φ=0,21, тому

см².

Виходячи із середнього значення А_бр, для цих двох випадків приймаємо 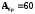см², тобто беремо двотавр №30а: А_бр=61,2 см², і_min=2,55 см. Тоді

.

За таблицею φ=0,30. Отже

МПа.

Оскільки перенапруженість складає всього близько 2%, то можна спинитися на двотаврі №30а.

Задача 15.2. Підібрати у вигляді чотирьох рівнобічних кутників (рис.15.4) поперечний переріз шарнірно обпертого стержня (колони) завдовжки 3,75 м, стиснутого силами Р=600 кН, якщо [σ]=160 МПа. Матеріал – ст.3.

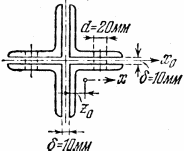
Рис. 15.4

Розв’язання. Нехай у першому наближенні φ₁=0,5. Тоді

см².

З таблиці сортаменту рівнобічних кутників вибираємо для чотирьох кутників необхідні дані: 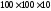мм з А₁=19,2 см², І_х=179 см⁴ і z₀=2,83 см. Для всього поперечного перерізу колони маємо

см².

Тоді 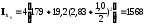см⁴. Радіус інерції поперечного перерізу

см.

Гнучкість колони

.

За таблицею значень для ст.3 знаходимо φ=0,732. Допустиме напруження дорівнює МПа.

Дійсне напруження МПа значно менше допустимого, а тому вибраний переріз буде недонапруженим.

Далі вибираємо кутники 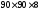мм із А₁=13,9 см², І_х=106 см⁴ і z₀=2,51 см. Для всього поперечного перерізу колони тепер маємо

см² і см⁴.

Радіус інерції поперечного перерізу:

см.

Гнучкість колони

.

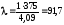За таблицею значень φ знаходимо φ=0,675. Тоді [σ_y]=0,675·160=108 МПа. Дійсне напруження

Мпа.

Можна спинитися на кутниках мм. Далі треба перевірити міцність колони, враховуючи отвори під заклепки. Площа поперечного перерізу дорівнює

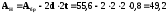см².

Стискуюче напруження з урахуванням отворів буде таким:

МПа.

Міцність матеріалу колони забезпечена.

Задача 15.4. Стальна балка прямокутного поперечного перерізу навантажена силами Р=70 кН і Р₁=500 Н (рис.15.5,а). Визначити найбільший прогин і максимальне нормальне напруження в балці. Як зміняться ці величини, якщо навантаження збільшити в 2,5 рази.

Рис. 15.5

Розв’язання. Максимальний прогин обчислюємо за наближеною формулою 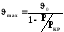, де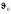- прогин від поперечного навантаження Р₁:

мм.

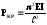- позначена так звана “ейлерова сила”, яка формально обчислюється як критична сила за Ейлером для стержня з шарнірними опорами:

кН;

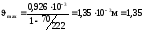мм.

Найбільший згинаючий момент, який виникає в середньому перерізі балки, обчислимо так:

Н·м.

Найбільше стискуюче напруження в цьому перерізі визначається за формулою

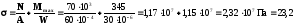МПа.

Якщо навантаження збільшити в 2,5 рази, то найбільший прогин буде

мм.

Найбільше стискуюче нормальне напруження

МПа.

Це напруження, подібно до прогинів і згинаючих моментів, залежить нелінійно від стискуючої сили: зміна навантаження в 2,5 рази викликає збільшення напруження σ майже в 5 разів, а прогину – у 8 разів.

164