
- •Міністерство освіти і науки україни
- •Моделювання систем
- •7.080401 «Інформаційні управляючі системи і технології»
- •Загальні положення
- •Продовження таблиці 1
- •Продовження таблиці 1
- •Методи моделювання рівномірного розподіленої випадкової величини на інтервалі [a, b]
- •Методи моделювання нормально розподіленої випадкової величини
- •Продовження таблиці 3
- •Продовження таблиці 3
- •Додаток 1
- •Список літератури
Методи моделювання рівномірного розподіленої випадкової величини на інтервалі [a, b]
Для
імітації
рівномірного
розподілу
в інтервалі
від [a, b]
використовується зворотне
перетворення функції
щільності
ймовірності(метод обернених
функцій). Розглянемо
загальний випадок
розподілу
випадкової величини(ВВ)
на
інтервалі
[a, b].
Неперервна
ВВ ![]() має
рівномірний
розподіл
в інтервалі
[a, b],
якщо її
функції
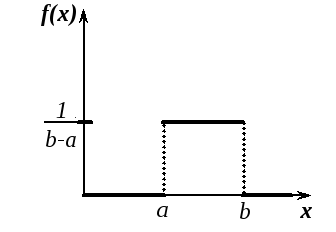
щільності (рис.
3.1) і розподілу
(рис. 3.2)
відповідно мають
вигляд:
має
рівномірний
розподіл
в інтервалі
[a, b],
якщо її
функції
щільності (рис.
3.1) і розподілу
(рис. 3.2)
відповідно мають
вигляд:
|
|
|
Рис. 3.1. Функція щільності для рівномірного розподілення
|
|
|
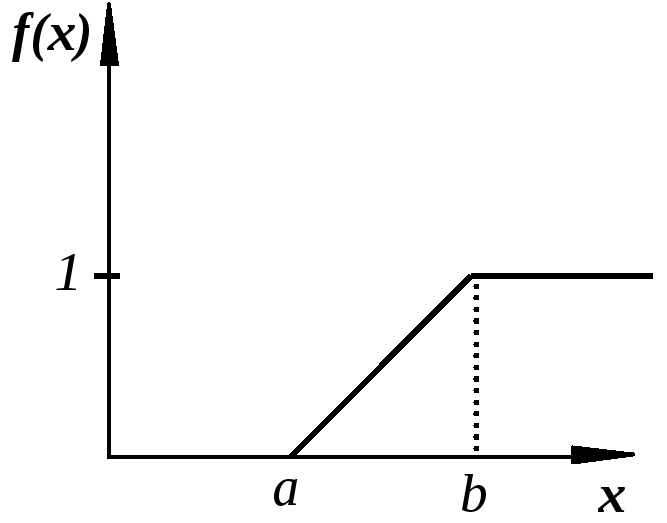
Рис. 3.2.Функція рівномірного розподілення
Виходячи з (3.2) маємо:
![]()
![]()
Тобто для генерації випадкових чисел {Хі} рівномірно розподілених на відрізку [a, b] будемо користуватися формулою:
![]()
де R - рівномірно розподілене псевдовипадкове число на [0, 1].
Методи моделювання нормально розподіленої випадкової величини
Метод Марсильї-Брея( метод полярних координат) відноситься до першого способу отримання послідовності псевдовипадкових чисел з нормальним законом розподілу. Метод обчислює дві незалежні нормально розподілені випадкові величини x1 і x2 із середнім значенням, рівним нулю, і середньоквадратичним відхиленням, рівним одиниці, по двох заданих незалежних рівномірно розподілених випадкових числах y1 і y2.х
Алгоритм методу:
1. Згенерувати два незалежних випадкових числа y1 і y2, рівномірно розподілених в інтервалі [0,1] (Використайте генератор random).
2. Визначити:
![]()
Обчислити:
![]()
Перевірити умову:
 Якщо "так",
то необхідно
повернутися
до кроку
1. Якщо
"ні", то переходимо
до кроку
5.
Якщо "так",
то необхідно
повернутися
до кроку
1. Якщо
"ні", то переходимо
до кроку
5.Обчислюємо x1и x2:
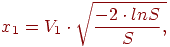
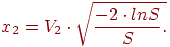
Отримані величини x1 і x2 - це потрібні значення нормально розподілених випадкових величин з середнім значенням рівним нулю(ɑ=0), і середньоквадратичним відхиленням(Ϭ=1).
При інших значеннях середнього та середньоквадратичного відхилення робимо перерахунок:
![]()
Метод Бокса-Маллера(модифікація метода полярних координат)
Метод полярних координат легко довести, скориставшись аналітичною геометрією. Розглянемо площину, визначену декартовими координатами V1 і V2. За допомогою кроків 1 і 2 раніш описаного методу ми отримуємо на площині рівномірно розподілені випадкові точки з декартовими координатами (V1, V2) і полярними координатами де
![]()
Далі, за допомогою кроків 3 і 4 методу, ми з цих випадкових точок залишаємо тільки ті точки, які знаходяться всередині одиничного кола.

Рис. 3.3. Геометрична інтерпретація метода
При цьому попадання точок всередину одиничного кола підкоряється закону нормального розподілу із середнім значенням рівним нулю, і середньоквадратичним відхиленням рівним одиниці.
Переходячи до полярних координатах точок, які рівномірно розподілені всередині одиничного кола маємо
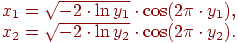
При значеннях середнього (ɑ) та середньоквадратичного відхилення(Ϭ) відмінних відповідно від 0 і 1 робимо перерахунок:
![]()
Метод, заснований на центральній граничній теоремі
Цей метод моделювання відноситься до третього способу отримання послідовності чисел з нормальним законом розподілу. Метод заснований на наближеному відтворенні умов, при яких справедлива центральна гранична теорема теорії імовірності.
Згідно центральної граничної теореми, при додаванні досить великої незалежних випадкових величин з довільним законом розподілу виходить випадкова величина, розподілена за нормальним законом. Досвід показує, що при додаванні всього шести (k = 6) випадкових величин рівномірно розподілених на інтервалі [0,1], виходить випадкова величина, яка з точністю, достатньою для більшості прикладних задач, може вважатися нормальною.
Розглянемо метод апроксимації нормально розподіленої випадкової величини Х, заснований на використанні дванадцяти (k = 12) рівномірно розподілених випадкових величин.
Алгоритм методу:
1. Скласти 12 рівномірно розподілених псевдовипадкових чисел yi( генеруються з допомогою генератора random ).
2. Пронормувати отриману суму, тобто отримати випадкову величину T з
М (Т) = 0 і, де Т - нормально розподілена випадкова величина.
3. Результат привести у відповідність із заданим математичним очікуванням і середньоквадратичним відхиленням.
Нормально розподілена випадкова величина X з необхідними значеннями математичного очікування і середньоквадратичного відхилення визначається як:
![]()
Нехай

де yi - незалежні рівномірно розподілені на інтервалі [0,1] випадкові величини.
Відомо, що математичне сподівання і дисперсія рівномірно розподіленим на інтервалі [0,1] випадкової величини Y відповідно рівні:
![]()
Тоді математичне сподівання суми Z дорівнює:
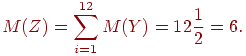
а її дисперсія D (Z) дорівнює:
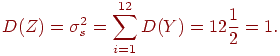
Пронормуємо суму Z, тобто перейдемо від неї до величини:
![]()
Переходячи до необхідних математичного сподівання a та середньоквадратичного відхилення, остаточно маємо:
![]()
Таким чином, щоб визначити значення нормально розподіленої випадкової величини з математичним очікуванням, рівним нулю, і середньоквадратичним відхиленням, рівним одиниці, необхідно взяти 12 рівномірно розподілених чисел, скласти їх, а з суми відняти 6, тобто:

Щоб визначити значення нормально розподіленої випадкової величини з необхідним математичним очікуванням ɑ і необхідним середньоквадратичним відхиленням Ϭ необхідно із суми дванадцяти рівномірно розподілених чисел відняти 6, а результат помножити на і додати a, тобто
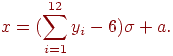
Моделювання
випадкових величин розподілених
за експоненційним
закономз
параметром
![]()
Щільність f (y) і функція F (y) цього розподілу мають вигляд (рис. 3.11):

Рис. 3.4. Щільність f (y) і функція F (y) експоненційного розподілу
Рішення

Оскільки
випадкова
величина
![]() має
рівномірний
розподіл
в інтервалі
[0,1], як
і
має
рівномірний
розподіл
в інтервалі
[0,1], як
і ![]() ,то
справедливо:
,то
справедливо:

Завдання . Генерація послідовності значень неперервної величини.
У відповідності із завданням (табл. 3) створити процедуру генерації послідовності значень неперервної величини X. Потужність послідовності, що генерується N=1000.
Таблиця 2
|
№ пор. |
Випадкова величина X | ||
|
Закон розподілення |
Метод |
Параметри | |
|
1 |
2 |
3 |
4 |
|
1 |
Рівномірний |
Метод обернених функцій |
A = 0, B = 6 |
|
2 |
Нормальний |
За центральною крайовою теоремою |
M = 5, = 3 |
|
3 |
Нормальний |
Метод Бокса-Маллера |
M = 4, = 0,3 |
|
4 |
Нормальний |
Метод Марсильї-Брея |
M = 2, = 0.1 |
|
5 |
Експоненціальний |
Логарифмічний метод |
= 8 |
|
6 |
Рівномірний |
Метод обернених функцій |
A = 2, B = 4 |
|
7 |
Нормальний |
За центральною крайовою теоремою |
M = 1, = 0,05 |
|
8 |
Нормальний |
Метод Бокса-Маллера |
M = 4, = 2 |
|
9 |
Нормальний |
Метод Марсильї-Брея |
M = 3, = 0.5 |
|
10 |
Експоненціальний |
Логарифмічний метод |
= 2 |
|
11 |
Рівномірний |
Метод обернених функцій |
A = 10, B = 15 |
|
12 |
Нормальний |
За центральною крайовою теоремою |
M = 13, = 2 |
|
13 |
Нормальний |
Метод Бокса-Маллера |
M = 1, = 0,7 |
|
14 |
Нормальний |
Метод Марсильї-Брея |
M = 50, = 10 |
|
15 |
Експоненціальний |
Логарифмічний метод |
= 3 |
|
16 |
Рівномірний |
Метод обернених функцій |
A = 50, B = 75 |
|
17 |
Нормальний |
За центральною крайовою теоремою |
M = 23, = 10 |
|
18 |
Нормальний |
Метод Бокса-Маллера |
M = 2, = 3 |
|
19 |
Нормальний |
Метод Марсильї-Брея |
M = 4, = 0,1 |
|
20 |
Експоненціальний |
Логарифмічний метод |
= 6 |
|
21 |
Рівномірний |
Метод обернених функцій |
A = 100, B = 150 |
|
22 |
Нормальний |
За центральною крайовою теоремою |
M = 6, = 2,5 |
|
23 |
Нормальний |
Метод Бокса-Маллера |
M = 1, = 7 |
|
24 |
Нормальний |
Метод Марсильї-Брея |
M = 15, = 10 |
|
25 |
Експоненціальний |
Логарифмічний метод |
= 4 |
Лабораторна робота №4. Побудова генераторів дискретних величин, із заданим законом розподілення
Теоретичні відомості.
Завдання2. Генерація послідовності значень дискретної величини.
У відповідності із завданням (табл. 3) створити процедуру генерації послідовності значень дискретної величини X. Потужність послідовності, що генерується N=1000. Знайти оцінку ймовірності появи випадкового числа M в згенерованій послідовності.
Таблиця 3
|
№ пор. |
Випадкова величина X | |||
|
Закон розподілення |
Метод |
Параметри |
M | |
|
1 |
2 |
3 |
4 |
5 |
|
1 |
Закон Пуассона |
Адитивний алгоритм |
=4 |
2 |
|
2 |
Закон Пуассона |
Мультиплікативний алгоритм |
=3 |
5 |
|
3 |
Біноміальний |
Алгоритм підрахунку успіхів |
N=100, P=0,67 |
1 |
|
4 |
Геометричний |
Метод обернених функцій |
P=0,35 |
0 |
|
5 |
Закон Пуассона |
Адитивний алгоритм |
=2 |
3 |
|
6 |
Закон Пуассона |
Мультиплікативний алгоритм |
=5 |
8 |
|
7 |
Біноміальний |
Алгоритм підрахунку успіхів |
N=100, P=0,7 |
0 |
|
8 |
Геометричний |
Метод обернених функцій |
P=0,5 |
7 |
|
9 |
Закон Пуассона |
Адитивний алгоритм |
=9 |
5 |
|
10 |
Закон Пуассона |
Мультиплікативний алгоритм |
=2 |
1 |
|
11 |
Біноміальний |
Алгоритм підрахунку успіхів |
N=100, P=0,05 |
4 |
|
12 |
Геометричний |
Метод обернених функцій |
P=0,7 |
7 |
|
13 |
Закон Пуассона |
Адитивний алгоритм |
=1 |
8 |
|
14 |
Закон Пуассона |
Мультиплікативний алгоритм |
=6 |
3 |

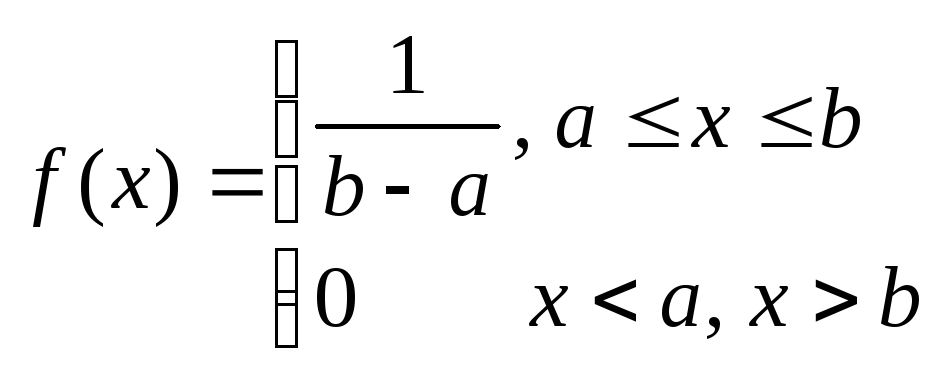
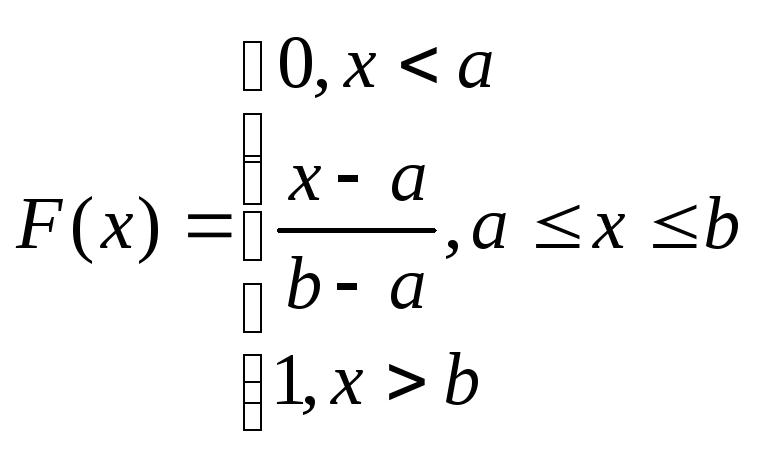 (3.2)
(3.2)