Продовження таблиці 1

Bapiант	[Xi, Xi+1]	N		Bapiант	[Xi, Xi+1]	N
17	0-1	289		18	0-5	15
	1-2	197			5-10	43
	2-3	139			10-15	25
	3-4	104			15-20	19
	4-5	100			20-25	31
	5-6	77			25-30	9
	6-7	70			30-35	14
	7-8	64			35-40	36
	8-9	52			40-45	21
19	2-5	1		20	0-10	313
	5-8	3			10-20	259
	8-11	5			20-30	145
	11-14	4			30-40	102
	14-17	10			40-50	74
	17-20	15			50-60	83
	20-23	14			60-70	51
	23-26	11			70-80	42
	26-29	8			80-90	34
	29-32	3			90-100	20
21	10,0-10,5	96		22	0-7	12
	10,5-11,0	81			7-14	10
	11,0-11,5	80			14-21	18
	11,5-12,0	79			21-28	25
	12,0-12,5	97			28-35	32
	112,5-13,0	88			35-42	30
	13,0-13,5	84			42-49	22
	13,5-14,0	78			49-56	16
	14,0-14,5	85			56-63	8
23	5-15	144		24	1-2	30
	15-25	100			2-3	45
	25-35	87			3-4	35
	35-45	68			4-5	50
	45-55	59			5-6	45
	55-65	50			6-7	51
	65-75	42			7-8	53
	75-85	29			8-9	28
	85-95	20			9-10	40

ТЕМА: Генерація випадкових величин, із заданим законом розподілення.

Генератор псевдовипадкових чисел (ГПВЧ, англ. Pseudorandom number generator, PRNG) - алгоритм, що генерує послідовність чисел, елементи якої майже незалежні один від одного і підкоряються заданому розподілу (зазвичай рівномірному).

Сучасна інформатика широко використовує псевдовипадкові числа в самих різних застосуваннях - від методу Монте-Карло та імітаційного моделювання до криптографії. При цьому від якості використовуваних ГПВЧ безпосередньо залежить якість одержуваних результатів. Цю обставину підкреслює відомий афоризм Роберта Р. Кавью з ORNL (англ.): «генерація випадкових чисел занадто важлива, щоб залишати її на волю випадку».

Задача отримання випадкових чисел , із заданим законом розподілення звичайно розбивається на дві. Спочатку отримують послідовність випадкових чисел {r}, рівномірно розподілених на проміжку (0,1). Потім з неї отримують послідовність випадкових чисел{x}, які мають заданий закон розподілення.

Лабораторна робота №2.

Побудова та дослідження генераторів базових

псевдовипадкових чисел.

Базові псевдовипадкові числа – це числа рівномірно розподілені на проміжку (0,1), що отримані на основі одного з методів машинної імітації.

Теоретичні відомості.

Алгоритмічні генератори випадкових чисел(ГВЧ)

Числа, які генеруються за допомогою цих ГВЧ, завжди є псевдовипадковими (або квазівипадковими), тобто кожне наступне згенероване число залежить від попереднього:

r_i + 1 = f(r_i) (2.1)

Послідовності, складені з таких чисел, як правило, утворюють петлі, тобто обов'язково існує цикл, що повторюється нескінченне число разів. Повторювані цикли називаються періодами.

Перевагою даних ГВЧ є швидкодія; генератори практично не вимагають ресурсів пам'яті, компактні. Недоліки: числа не можна повною мірою назвати випадковими, оскільки між ними є залежність, а також наявність періодів в послідовності квазівипадкових чисел.

Розглянемо кілька алгоритмічних методів отримання ГВЧ:

• метод серединних квадратів;

• метод серединних добутків;

• метод перемішування;

• лінійні конгруентні методи;

• нелінійні конгруентні методи.

Метод серединних квадратів

Є деяке чотиризначне число R0. Це число підноситься до квадрату і заноситься в R1. Далі з R1 береться середина (чотири середні цифри) - нове випадкове число - і записується в R0. Потім процедура повторюється (див. рис. 2.1). Зазначимо, що насправді в якості випадкового числа необхідно брати не ghij, а 0.ghij - з приписаним зліва нулем і десятковою крапкою. Цей факт відображено як на рис. 22.6, так і на наступних подібних малюнках.

Рис. 2.1. Схема методу серединних квадратів

Недоліки методу:

1) якщо на деякій ітерації число R0 стане рівним нулю, то генератор вироджується, тому важливим є правильний вибір початкового значення R0,

2) генератор буде повторювати послідовність через Mn кроків (в кращому випадку), де n - розрядність числа R0, M - заснування системи числення.

Метод серединних добутків

Число R0 множиться на R1, з отриманого результату R2 витягується середина R2* (це чергове випадкове число) і множиться на R1. За цією схемою обчислюються всі наступні випадкові числа (див. рис. 2.2).

 

Рис. 2.2. Схема методу серединних добутків

Метод перемішування

У методі перемішування використовуються операції циклічного зсуву вмісту комірки вліво і вправо. Ідея методу полягає в наступному. Нехай в комірці зберігається початкове число R0. Циклічно зрушуючи вміст комірки ліворуч на 1/4 довжини комірки отримуємо нове число R0*. Точно так само, циклічно зрушуючи вміст комірки R0 вправо на 1/4 довжини комірки, отримуємо друге число R0**. Сума чисел R0* і R0** дає нове випадкове число R1. Далі R1 заноситься в R0, і вся послідовність операцій повторюється (див. рис. 2.3).

Рис. 2.3. Схема методу перемішування

Зверніть увагу, що число, отримане в результаті додавання R0* і R0**, може не вміститися повністю в комірці R1. У цьому випадку від отриманого числа повинні бути відкинуті зайві розряди. Пояснимо це на рис. 2.3, де всі комірки представлені вісьмома двійковими розрядами. Нехай R0* = 100100012 = 14510, R0** = 101000012 = 16110, тоді R0 * + R0 ** = 1001100102 = 30610. Як бачимо, число 306 займає 9 розрядів (у двійковій системі числення), а комірка R1 (як і R0) може вмістити в себе максимум 8 розрядів. Тому перед занесенням значення в R1 необхідно прибрати один «зайвий», крайній лівий біт з числа 306, в результаті чого в R1 піде вже не 306, а 001 100 102 = 5010. Також зауважимо, що в таких мовах, як Паскаль, «урізання» зайвих бітів при переповненні комірки проводиться автоматично відповідно до заданого типом змінної.

Конгруентні методи

Тепер майже всі стандартні бібліотечні програми обчислення послідовності рівномірно розподілених випадкових чисел грунтуються на конгруентних методах. Найвідомішими є такі конгруентні методи: мультиплікативний, мішаний і адитивний.

Конгруентні методи базуються на використанні операції mod (x, y), яка повертає залишок від ділення першого аргументу на другий.

Мішаний конгруентний метод

Кожне наступне випадкове число розраховується на основі попереднього випадкового числа за такою формулою:

r_i+1 = (k • r_i + b) mod M , (2.2)

де M - модуль (0 <M);

k - множник (0 ≤ k <M);

b - приріст (0 ≤ b <M);

r0 - початкове значення (0 ≤ r0 <M).

Згідно зформулою (2.2) для знаходження наступного випадкового числа достатньо виконати такі дії:

1) взяти останнє випадкове число ;

2) помножити його на коефіцієнт k;

3) добуток поділити на модуль M;

4) остачу від ділення вважати шуканим випадковим числом ;

це буде одне з цілих чисел 0, 1, 2, 3, ..., M – 1.

Для якісного генератора потрібно підібрати відповідні коефіцієнти. Як правило, це великі прості числа. Необхідно, щоб число M було досить великим, тому що період не може мати більше M елементів.

Мультиплікативний конгруентний метод

Багато авторів називають лінійну конгруентних послідовністьодержану за формулою (6.2) при b = 0 мультиплікативним конгруентним методом.

r_i+1 = (k • r_i) mod M (2.3)

Адитивний конгруентний метод

В основу цього методу покладено рекурентне співвідношення

r_i+1 = (r_i + r_i-1) mod M (2.4)

Нелінійні конгруентні генератори

Іноді використовують квадратичні і кубічні конгруентні генератори, які мають більшу стійкість до злому.

Квадратичний конгруентний генератор має вигляд

X_k+1 = (aX_k² +bX_k +c) mod M (2.5)

Кубічний конгруентний генератор задається як

X (aX_k³ + bX_k² +cX_k + d) mod M (2.6)

Перевірка якості роботи генератора

Ефективність статистичного моделювання систем на ЕОМ і достовірність отриманих результатів залежить від якості вихідних (базових) послідовностей псевдовипадкових чисел, які є основою для отримання стохастичних впливів на елементи моделюється. Тому перед моделюванням на ЕОМ необхідно переконатися в тому, що вихідна послідовність псевдовипадкових чисел задовольняє висунутим до неї вимогам.

При моделюванні важливими характеристиками якості генератора є довжина періоду p і довжина відрізка аперіодічності L.(див. рис.2.4)

Довжина відрізка аперіодічності L псевдослучайной послідовності є найбільше ціле число, таке, що всі числа xi в межах цього відрізка не повторюються.

Спосіб експериментального визначення довжини періоду p і довжини відрізка аперіодічності L зводиться до наступного:

1. Запускається програма генерації послідовності {Xi} з початковим значенням X₀ і генерується V чисел Xi. У більшості випадків V = (1 - 5) 10⁶. Генеруються числа і фіксується число X_v.

2. Потім програма запускається повторно з початковим числом X₀ і при генерації чергового числа перевіряється істинність події p {X_i = X_V}. Якщо ця подія істинна при

i = i1 та i = i2 (i1 <i2 <V), то обчислюється довжина періоду послідовності p = i2 - i1.

3. Проводиться запуск програми генерації з початковими числами X₀ і X_P. При цьому фіксується мінімальний номер i = i3, при якому істинна подія { X_i = X_P+i }, і обчислюється довжина відрізка аперіодічності L = i3 + p.

Рис. 2.4. Подання визначення довжин періоду P

і відрізка періодичності L

Застосовувані в імітаційному моделюванні генератори випадкових чисел повинні пройти тести на придатність.Існують тести двох типів.

Емпіричні тести - це звичайний тип статистичних тестів, вони засновані на дійсних значеннях Xi, які видаються генератором.

Теоретичні тести не є тестами в тому сенсі, в якому вони передбачаються в статистиці. Проте в них використовуються числові параметри, щоб оцінити генератор глобально без фактичного генерування декотрих або всіх значень Xi.

Основні характеристики, які аналізуються для оцінки якості генератора випадкових чисел:

- Рівномірність;

- Стохастичність (випадковість);

- Незалежність.

Розглянемо методи проведення такого аналізу, що найбільш часто застосовуються на практиці.

Перевірка рівномірності

Перевірка рівномірності може бути виконана за допомогою гістограми відносних частот значень випадкової величини, що генерується. Для її побудови інтервал (0; 1) розбивається на m рівних частин і підраховується відносна кількість попадань значень випадкової величини в кожен інтервал. Чим ближче вигляд гістограми до прямої, тим більшою мірою послідовність, що генерується відповідає вимозі рівномірності розподілу (рис. 2.5).

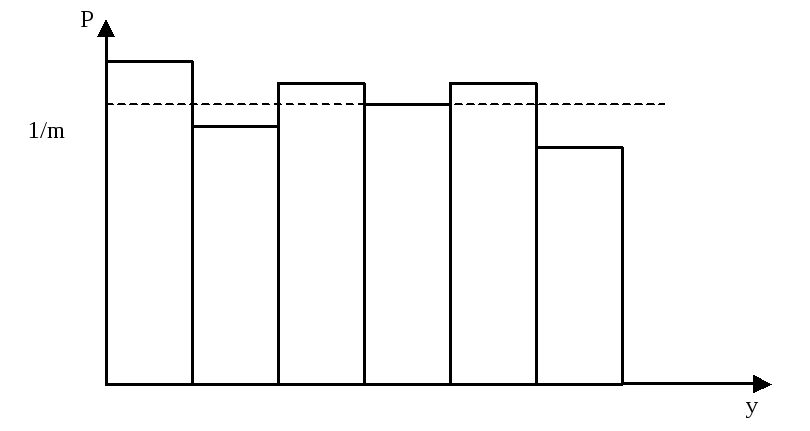
Рис. 2.5. Гістограма відносних частот випадкових чисел

Або

ГВЧ повинен видавати близькі до наступних значення статистичних параметрів, характерних для рівномірного випадкового закону:

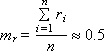—математичнеочікування; (2.7)

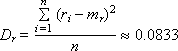—дисперсія; (2.8)

—середньоквадратичневідхилення. (2.9)

Розрахунковий частотний тест

Частотний тест дозволяє з'ясувати, скільки чисел потрапило в інтервал (mr - σr; mr + σr), тобто (0.5 - 0.2887; 0.5 + 0.2887) або, зрештою, (0.2113; 0.7887). Так як 0.7887 - 0.2113 = 0.5774, укладаємо, що в хорошому ГВЧ в цей інтервал має потрапляти близько 57.7% з усіх випали випадкових чисел (див. рис. 2.6).

Рис. 2.6. Частотна діаграма ідеального ГВЧ у разі перевірки його на частотний тест

Також необхідно враховувати, що кількість чисел, які потрапили в інтервал (0; 0.5), має бути приблизно рівна кількості чисел, що потрапили в інтервал (0.5, 1).

Перевірка за критерієм «хі-квадрат»

Критерій «хі-квадрат» (χ²-критерій) - це один з найвідоміших статистичних критеріїв; він є основним методом, використовуваним в поєднанні з іншими критеріями. Критерій «хі-квадрат» був запропонований в 1900 році Карлом Пірсоном. Його чудова робота розглядається як фундамент сучасної математичної статистики.

Для нашого випадку перевірка за критерієм «хі-квадрат» дозволить дізнатися, наскільки створений нами реальний ГВЧ близький до еталону ГВЧ, тобто задовольняє він вимогу рівномірного розподілу чи ні.

Частотна діаграма еталонного ГВЧ представлена на рис. 2.7. Так як закон розподілу еталонного ГВЧ рівномірний, то (теоретична) ймовірність pi потрапляння чисел в i-ий інтервал (всього цих інтервалів k) дорівнює pi = 1 / k. І, таким чином, у кожний з k інтервалів потрапить рівно по pi · N чисел (N - загальна кількість згенерованих чисел).

Рис. рис. 2.7. Частотна діаграма еталонного ГВЧ

Реальний ГВЧ видаватиме числа, розподілені (причому, не обов'язково рівномірно!) по k інтервалах і в кожен інтервал потрапить по ni чисел (в сумі n1 + n2 + ... + nk = N). Як же нам визначити, наскільки випробовуваний ГВЧ хороший і близький до еталонного? Цілком логічно розглянути квадрати різниць між отриманим кількістю чисел ni і «еталонним» pi · N. Складемо їх, і в результаті одержимо:

χ²_експ. = (N1 - p1·N) ² + (n2 - p2·N) ² + ... + (nk - pk·N) ² (2.10)

З цієї формули випливає, що чим менше різниця в кожному з доданків (а значить, і чим менше значення χ²_експ..), Тим сильніше закон розподілу випадкових чисел, що генеруються реальним ГВЧ, тяжіє до рівномірного.

У попередньому виразі кожному з доданків приписується однакову вагу (рівний 1), що насправді може не відповідати дійсності, тому для статистики «хі-квадрат» необхідно провести нормування кожного i-го доданка, поділивши його на pi · N:

(2.11)

Нарешті, запишемо отримане вираження більш компактно і спростимо його:

(2.12)

Ми отримали значення критерію «хі-квадрат» для експериментальних даних.

У табл.1 з Додатку1 наведені теоретичні значення «хі-квадрат» (χ²теор.), де ν = k - 1 - це число ступенів свободи, p - це довірча ймовірність, що задається користувачем, який вказує, наскільки ГВЧ повинен задовольняти вимогам рівномірного розподілу, або p - це ймовірність того, що експериментальне значення χ²експ. буде менше табульованого (теоретичного) χ²теор. або дорівнює йому.

Прийнятним вважають p від 10% до 90%.

Якщо χ²_експ.. багато більше χ²_теор. (тобто p - велике), то генератор не задовольняє вимогу рівномірного розподілу, оскільки спостережувані значення ni занадто далеко йдуть від теоретичних p_i·N і не можуть розглядатися як випадкові. Іншими словами, встановлюється такий великий довірчий інтервал, що обмеження на числа стають дуже нежорсткими, вимоги до чисел - слабкими. При цьому буде спостерігатися дуже велика абсолютна похибка.

Ще Д. Кнут у своїй книзі «Мистецтво програмування» зауважив, що мати χ2експ. маленьким теж, загалом-то, недобре, хоча це й здається, на перший погляд, чудово з точки зору рівномірності. Дійсно, візьміть ряд чисел 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, ... - вони ідеальні з точки зору рівномірності, і χ2експ. буде практично нульовим, але навряд чи ви їх визнаєте випадковими.

Якщо χ²_експ.. багато менше χ²_теор. (тобто p - мале), то генератор не задовольняє вимогу випадкового рівномірного розподілу, оскільки спостережувані значення ni занадто близькі до теоретичних pi · N і не можуть розглядатися як випадкові.

А от якщо χ²_експ.. лежить в деякому діапазоні, між двома значеннями χ²_теор., які відповідають, наприклад, p = 25% і p = 50%, то можна вважати, що значення випадкових чисел, що породжуються датчиком, цілком є випадковими.

При цьому додатково треба мати на увазі, що всі значення pi · N повинні бути досить великими, наприклад більше 5 (з'ясовано емпіричним шляхом). Тільки тоді (за досить великий статистичної вибірці) умови проведення експерименту можна вважати задовільними.

Отже, процедура перевірки має наступний вигляд.

    Діапазон від 0 до 1 розбивається на k рівних інтервалів.

    Запускається ГВЧ N раз (N повинно бути велике, наприклад, N / k> 5).

    Визначається кількість випадкових чисел, що потрапили в кожен інтервал:

ni, i = 1, ..., k.

    Обчислюється експериментальне значення χ2експ. за наступною формулою:

(2.13)

где p_i = 1/k - теоретична ймовірність попадання чисел в k-ий інтервал.

    Шляхом порівняння експериментально отриманого значення χ²_експ. з теоретичним χ²_теор. (з табл.1 Додатку1) робиться висновок про придатність генератора для використання. Для цього:

а) знаходимо в табл.1 Додатку1 (рядок = кількість інтервалів - 1);

б) порівнюємо обчислене χ²_експ.. з χ²_теор., що зустрічаються в рядку. При цьому можливі три випадки.

    Перший випадок: χ²_експ.. багато більше будь-якого χ²_теор. в рядку - гіпотеза про випадковість рівномірного генератора не виконується (розкид чисел занадто великий, щоб бути випадковим).

    Другий випадок: χ²_експ.. багато менше будь-якого χ²_теор. в рядку - гіпотеза про випадковість рівномірного генератора не виконується (розкид чисел занадто малий, щоб бути випадковим).

    Третій випадок: χ²_експ.. лежить між значеннями χ²_теор. двох колонок, що стоять поруч - гіпотеза про випадковість рівномірного генератора виконується з імовірністю p (тобто в p випадках зі 100).

    Зауважимо, що чим ближче виходить p до значення 50%, тим краще.

Завдання.

• створити процедуру генерації базових псевдовипадкових чисел за завданням ( див. Табл2.1). Потужність послідовності, що генерується N=1000.

• обчислити (алгоритмічно) довжину періоду P та відрізку аперіодичності L для отриманої послідовності.

• оцінити рівномірність отриманої послідовності.

Варіанти завдання Таблиця 2

№ вар	Правило генерації псевдовипадкових чисел	Метод оцінки рівномірності
1	Метод “серединних квадратів” (для 4-значних чисел)	гістограма відносних частот
2		Розрахунковий частотний тест
3		критерій «хі-квадрат»
4		гістограма відносних частот
5	Метод “серединних добутків” (для 4-значних чисел)	Розрахунковий частотний тест
6		критерій «хі-квадрат»
7		гістограма відносних частот
8		Розрахунковий частотний тест
9		критерій «хі-квадрат»
10	Метод перемішування (для 8-значних чисел)	гістограма відносних частот
11		Розрахунковий частотний тест
12		критерій «хі-квадрат»
13		гістограма відносних частот
14	Кубічний конгруентний метод	Розрахунковий частотний тест
15		критерій «хі-квадрат»
16		гістограма відносних частот
17		Розрахунковий частотний тест
18		критерій «хі-квадрат»
19	Квадратичний конгруентний метод	гістограма відносних частот
20		Розрахунковий частотний тест
21		критерій «хі-квадрат»
22		гістограма відносних частот
23	Мішаний конгруентний метод	Розрахунковий частотний тест
24		критерій «хі-квадрат»
25		Гістограма відносних частот
26		Розрахунковий частотний тест
27	Мультиплікативний конгруентний метод	критерій «хі-квадрат»
28		Гістограма відносних частот
29		Розрахунковий частотний тест
30	Адитивний конгруентний метод	критерій «хі-квадрат»

Лабораторна робота №3. Побудова генераторів дійсних величин, із заданим законом розподілення

Теоретичні відомості.

У всіх сучасних середовищах програмування існують функції, які генерують випадкові числа. Найчастіше це бувають випадкові числа рівномірно розподілені на відрізку [0:1]. Рівномірний розподіл означає, що згенероване випадкове число може потрапити в будь-яку точку інтервалу [0:1] з рівною ймовірністю.Однак, для потреб моделювання одного рівномірного (uniform, англ.) розподілу недостатньо.

В основі моделювання випадкових величин з довільними законами розподілу ймовірностей лежить, як правило, метод зворотної функції.У цьому методі використо-вується наступна теорема.

Теорема. Якщо випадкова величина Yмає щільність розподілу ймовірностей, то розподіл випадкової величини

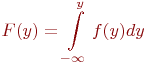(3.1)

є рівномірним на інтервалі[0, 1],

т. ч. теорема може бутипроілюстрована графіками:

Рис. 3.1.Ілюстраціядометоду оберненоїфункції

Позначимо:--е число из,--евипадковечислоіздовільногорозподілення. Із (3.1) слідує:

ВідносноYiвираз приймає вигляд:

Звідси і назва – «метод оберненої функції»

Розглянемо методи генерації дійсних(неперервних) величин з різними законами розподілення.