§2. Термодинаміка

Зв’язок між молярною та питомоюс теплоємностями газу:

, (2.32)

де М – молярна маса.

Молярні теплоємності при постійному тиску відповідно дорівнюють:

, (2.33)

де і – число ступенів вільності; R – молярна газова стала.

Питомі теплоємності при постійному об’ємі та постійному тиску відповідно дорівнюють:

. (2.34)

Рівняння Майєра:

. (2.35)

Показник адіабати: . (2.36)

Внутрішня енергія ідеального газу:

. (2.37)

Робота, пов’язана зі зміною об’єму газу, в загальному випадку обчислюється за формулою:

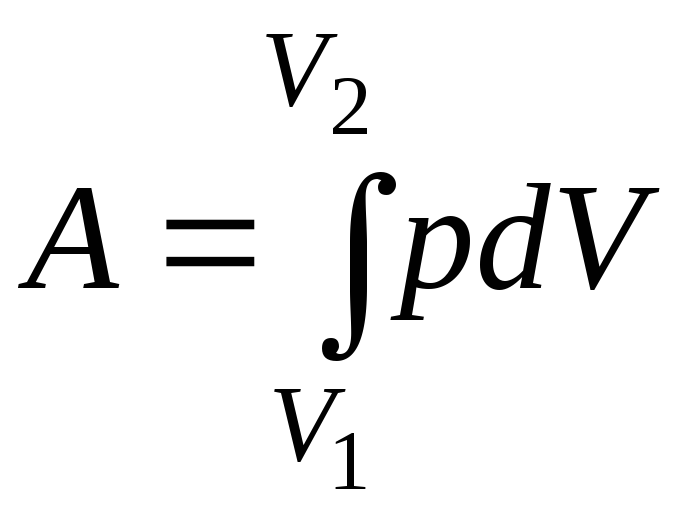, (2.38)

де – початковий об’єм газу;– його кінцевий об’єм.

Робота при ізобаричному процесі (р = const):

; (2.39)

при ізотермічному процесі (T = const):

; (2.40)

при адіабатичному процесі:

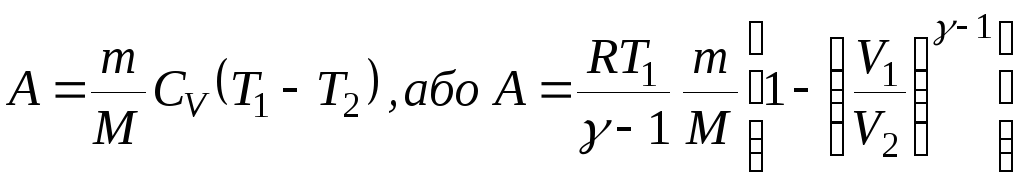; (2.41)

де – початкова температура газу;– його кінцева температура.

Рівняння Пуассона (адіабатичний процес):

. (2.42)

Зв’язок між початковим та кінцевим значенням параметрів стану газу при адіабатичному процесі:

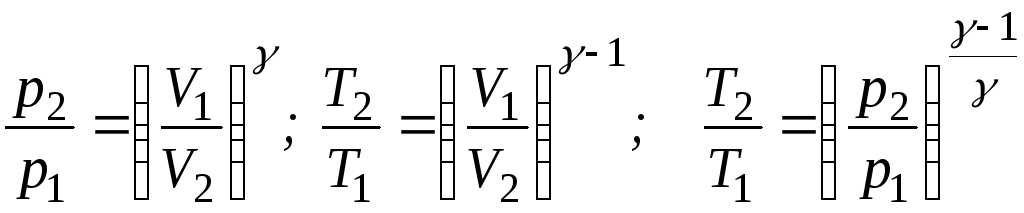(2.43)

I-й закон термодинаміки в загальному випадку має вигляд:

, (2.44)

де Q – кількість теплоти, що надається газу; – зміна його внут-рішньої енергії;A – робота, що виконується газом проти зовнішніх сил.

I-й закон термодинаміки при ізобарному процесі:

; (2.45)

при ізохорному процесі (А = 0):

; (2.46)

при ізотермічному процесі (U = 0):

; (2.47)

при адіабатному процесі (Q = 0):

. (2.48)

Термічний коефіцієнт корисної дії (к. к. д.) циклу в загальному випадку:

, (2.49)

де – кількість теплоти, отримана робочим тілом (газом) від нагрівача;– кількість теплоти, що передана робочим тілом охолоджувачу.

К.к.д. циклу Карно:

, або , (2.50)

де – температура нагрівача;– температура холодильника.

Зміна ентропії:

, (2.51)

де A і В – межі інтегрування, що відповідають початковому та кінце-вому станам системи. Оскільки процес рівноважний, то інтегрування проводять по будь-якому шляху.

Формула Больцмана:

S = k ln W , (2.52)

де S – ентропія системи, W – термодинамічна імовірність її стану, k – стала Больцмана.

Коефіцієнт поверхневого натягу:

, (2.53)

де F – сила поверхневого натягу, що діє на контур; l – довжина контуру рідини, – зміна вільної енергії поверхневої плівки рідини, пов’язана зі зміною площіповерхні цієї плівки.

Формула Лапласа виражає тиск р, який створюється сферичною поверхнею рідини:

, (2.54)

де R – радіус сферичної поверхні.

Висота підйому рідини в капілярній трубці:

, (2.55)

де – крайовий кут (при повному змочуванні стінок трубки рідиною;при повному незмочуванні);R – радіус каналу трубки; – густина рідини;g – прискорення вільного падіння.

Висота підйому рідини між двома близькими і паралельними одна одній площинами:

, (2.56)

де d – відстань між площинами.