1.5.2 Зведення багатокритеріальної задачі до однокритеріальної

Найбільш поширеним евристичним прийомом вирішення тієї чи іншої конкретної багатокритеріальної задачі є її зведення до рішення деякої скалярної (однокритеріальної) задачі, цільова функція якої найчастіше являє собою певну комбінацію наявних критеріїв 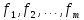. Такий прийом носить назву скаляризації багатокритеріальної задачі. Залежно від способу комбінування наявних декількох критеріїв в єдиний скалярний, отримуємо той чи інший тип скаляризації, який обираємо виходячи із суті розв'язуваної задачі і наявності додаткової інформації про переваги.

Найпростіший спосіб скаляризації заснований на використанні так званої лінійної згортки критеріїв

На практиці процес скаляризації починають з підбору коефіцієнтів лінійної згортки, тобто чисел Ці числа трактують, як якісь «ваги» або «коефіцієнти важливості» відповідних критеріїв, так що більш важливому з них призначають більший коефіцієнт в лінійній згортці критеріїв, а менш важливому–менший.

Метод має наступні недоліки:

1. Низьку оцінку по одному критерію можна компенсувати високою оцінкою по-іншому.

2. Не завжди вдається коректно оцінити вагу критеріїв.

Зведемо багатокритеріальну задачу до однокритеріальної за допомогою методу лінійної згортки.

Математична модель задачі багатокритеріальної оптимізації має наступний вигляд:

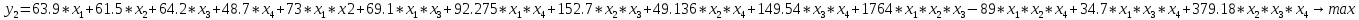
Задаємо вагові коефіцієнти, які визначають ступінь важливості кожного критерію:

Мінімізуємо лінійну комбінацію цільових функцій, тобто розв’язуємо задачу:

Одержуємо математичну модель задачі однокритеріальної оптимізації наступного вигляду:

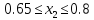
1.5.3 Однокритеріальна оптимізація системи

Задача однокритеріальної оптимізації формулюється наступним чином: мінімізувати задану функцію , де – область допустимих значень функції . Рішенням є для всіх .

Пошук рішень в однокритеріальних задачах (задачах скалярної оптимізації) залежить від виду математичної моделі і опису її виразів. Це можуть бути наступні задачі оптимізації:

• пошуку екстремуму алгебраїчної функції – залежності критерію від параметрів системи . Для задачі із плавною зміною функції екстремум знаходиться диференціюванням. Рішення– конкретне чисельне значення;

• варіаційного числення, якщо критерій описується функціоналом, тобто інтегралом від виразу, що залежить від параметрів, їх функції і похідних. Рішення має вигляд функціональної залежності (аналітичного рівняння);

• лінійного програмування, коли критерій та умови, що накладаються на вирішення задачі, є лінійними функціями параметрів (рівності або нерівності). Рішення – чисельне значення;

• нелінійного програмування;

• пошуку варіантів рішень методами повного або часткового перебору.

Задачі однокритеріальної оптимізації діляться на задачі умовної (шукається оптимальне рішення, що задовольняє деякі обмеження і цільову функцію) і безумовної (коли шукається оптимальне рішення, що задовольняє цільову функцію) оптимізації.

1. Задача умовної оптимізації.

Це задача, що пов'язана з оптимізацією при наявності деякої кількості обмежень на керовані змінні. Такі обмеження істотно зменшують розміри області, в якій шукається оптимум. Процес оптимізації стає більш складним, оскільки за наявності обмежень не можна використовувати застосовувані умови оптимальності. При цьому може порушуватися навіть основна умова, відповідно до якої оптимум повинен досягатися в стаціонарній точці.

Методи умовної оптимізації:

• Задачі з обмеженнями у вигляді рівностей (Множники Лагранжа);

За допомогою методу множників Лагранжа по суті встановлюються необхідні умови, що дозволяють ідентифікувати точки оптимуму в задачах оптимізації з обмеженнями-рівностями. При цьому задача з обмеженнями перетворюється в еквівалентну задачу безумовної оптимізації, в якій фігурують деякі невідомі параметри, звані множниками Лагранжа.

• Задачі з обмеженнями у вигляді нерівностей;

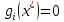Як і в попередньому методі, встановлюються необхідні умови, що дозволяють ідентифікувати точки оптимуму в задачах оптимізації з обмеженнями, але вже у вигляді нерівностей. У точці локального мінімуму задачі, кожне з обмежень виконується або у вигляді рівності, або у вигляді нерівності. Обмеження першого виду називаються активними обмеженнями. Інші обмеження називаються неактивними обмеженнями. Велике значення в теорії та обчислювальній практиці має теорема Куна–Таккера для задачі умовної оптимізації з обмеженнями типу нерівностей.

• Методи штрафних функцій;

Основна задача методу штрафних функцій полягає в перетворенні задачі мінімізації функції , з відповідними обмеженнями, накладеними на, в задачу пошуку мінімуму без обмежень функції.

Функція є штрафною. Необхідно, щоб при порушенні обмежень вона «штрафувала» функцію, тобто збільшувала її значення. В цьому випадку мінімум функціїбуде знаходитися всередині області обмежень. Функція, що задовольняє цій умові, може бути не єдиною. Задачу мінімізації можна сформулювати наступним чином:

мінімізувати функцію , при обмеженнях.

Функцію зручно записати наступним чином:,

де –позитивна величина.

Тоді функція приймає вид

 

Якщо приймає допустимі значення, тобто значення, для яких , то приймає значення, які більші відповідних значень (істинної цільової функції даної задачі), і різницю можна зменшити за рахунок того, що може бути дуже малою величиною. Але якщоприймає значення, які хоч і є допустимими, але близькі до межі області обмежень, і принаймні одна з функційблизька до нуля, тоді значення функції, і отже значення функціїстануть дуже великі. Таким чином, вплив функціїполягає у створенні «гребеня з крутими краями» уздовж кожної межі області обмежень. Отже, якщо пошук почнеться з допустимої точки і здійснюється пошук мінімуму функціїбез обмежень, то мінімум, звичайно, буде досягатися всередині допустимої області для задачі з обмеженнями. Вважаючидостатньо малою величиною, для того щоб впливбув малим в точці мінімуму, ми можемо зробити точку мінімуму функціїбез обмежень, що співпадатиме з точкою мінімуму задачі з обмеженнями.

• Метод факторів.

Своєрідним і дуже ефективним методом штрафів є метод факторів (або множників), який заснований на штрафі типу "квадрат зрізання" для обмежень-нерівностей.

2. Задача безумовної оптимізації.

Задачі безумовної оптимізації – це такі, у яких задана лише одна цільова функція. В цих задачах не існує обмежень та граничних умов. Модель безумовної оптимізації має теоретичний характер, тому що на практиці граничні умови задаються завжди. У даних задачах поняття екстремуму й оптимуму збігаються, і для знаходження оптимуму у них використовуються методи знаходження екстремуму.

Методи безумовної оптимізації поділяються на багатопараметричні й однопараметричні. У задачах багатопараметричної оптимізації цільова функція є функцією декількох керованих параметрів, а в задачах однопараметричної оптимізації – функцією одного керованого параметра.