Варианты 11.1 - 11.3

Пусть непилотируемый летательный аппарат, запускаемый с земли, должен за время Т, кратное t, достигнуть высоты Н. Сигнал коррекции траектории поступает через интервалы t и мгновенно отрабатывается. Между корректировками полет идет под одним углом к горизонту. Известны зависимости:

; ,

где q - расход горючего, кг/с; h - высота аппарата относительно земли, м; v - скорость полета, км/ч;  - угол подъема (спуска), град;

Требуется найти оптимальную траекторию полета с точностью не хуже 4% от Н и соответствующее ей (оптимальное) значение Т; построить графики траектории в координатах “высота - время” и “высота - расстояние по земле от точки старта”.

Значения параметров приведены в табл. 16.

Таблица 16

Вариант	Н, м	t,с	а0, кг/с	а1, кг/(сград2)	а2, кг/(см)	в0, км/ч	в1, км/(чград)
11.1	9600	10	12	10-2	10-3	3000	30
11.2	4800	5	12	10-2	10-3	3000	30
11.3	12000	20	12	10-2	10-3	3000	30

Варианты 12.1 - 12.3

На кондитерской фабрике организуется выпуск трех видов продукции из двух видов сырья. Известны нормы расхода сырья на изготовление единицы продукции и количество имеющегося сырья (табл. 17). Зависимость прибыли от объема производства каждого вида продукции дана в табл. 18.

Требуется определить оптимальный план производства продукции.

Указание: использовать прием снижения размерности на основе множителей Лагранжа.

Таблица 17

Вид сырья	Расход на единицу продукции (по вариантам)			Кол-во сырья (по вариантам)
	1-й вид	2-й вид	3-й вид
I	2; 5; 3	3; 1; 2	1; 2; 4		10; 9; 8
II	4; 2 ; 3	2; 4; 5	3; 2; 1		12; 10; 11

Таблица 18

Вид продукции	Вариант 12.1	Вариант 12.2	Вариант 12.3
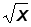
I	8	20(1-е - 0,3х)	12х-х2
II	1,2х2	9х-х2	7х
III	8х-х2	3х	1,5х2

Варианты 13.1 - 13.3

Два вида средств в количестве P и Q, выделенных предприятию на квартал, необходимо распределить по месяцам. Прибыль за месяц зависит от величины использованных средств, как показано в табл. 19, где х и у - количества 1-го и 2-го вида средств, используемых в соответствующий месяц. На каждый месяц должно быть выделено не менее одной единицы первого вида средств.

Указание: использовать прием снижения размерности на основе множителей Лагранжа. При этом невязка по сумме средств не должна быть больше 3%.

Таблица 19

Вариант	1-й месяц	2-й месяц	3-й месяц	P	Q
13.1	1,5х+10	5	6+10у-у2	5	4
13.2	5+2	2х	0,5х(12у-2у2)	6	5
13.3	10	+10	5+8у-у2	5	6