Лекции / Лекци4

Лекция 4

Пороха прогрессивной формы.

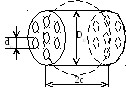
В этих порохах (t), достигается увеличением чисел каналов 7, 14. Рассмотрим три формы пороха.

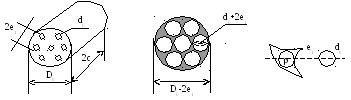1. Цилиндрическое зерно с 7-ю каналами.

Установлено практикой что: d₀=e₁; D₀=3d₀+4.2e₁=11d₀; 2c=(2.02.5)D₀.

При горении происходит распад на 12 прутиков или призмочек (лучинок). Они горят дегрессивно.

_s – сгоревшая часть к моменту распада.

_s – относительная поверхность в момент распада.

z_s=1; e_k=e₁+ и z_k>1;  -толщина элементов распада.

Для стандартного зерна _s=S_s/S₁=1.37; _s=0.85. Сначала догорают продукты распада.

’=0.23e₁; затем =0.532e₁, тогда e_k=e₁+; z_k=1+/e₁=1.532.

выражения (z) и (z) те же но <1;  >0; <0;

=z(1+z+z²); =1+2z+3z².

2. З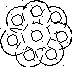ерно Уолша.

d₀=e₁; 2c=(2025)d₀. Наружная поверхность образуется 6-ю цилиндрическими поверхностями, описанными из центра каждого из 6-ти наружных каналов.

В момент распада образуется 12 почти одинаковых призмочек ’=0.23e₁; e_k=e₁+’=1.23e₁; z_k=1.23; _s=0.95; _s=1.37; =(S₁/₁)e₁ и _I=0.72; _II=1.23 т.к. пороха имеют одну и ту же поверхность, но объем II-го зерна меньше.

2. Зерно Киснемского (36 квадратных каналов).

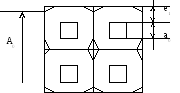
В 1919 г. 2c5A₀=100a₀; _s=0.9; ”=(2-1)e₁=0.41e₁; z_k=1+(”/e₁)=1.2;

_s=2 ( лаборант Циалов).

№	порох	s	s		zk
1	7-ми канальный	0.85	1.37	0.72	1.53
2	Уолша	0.95	1.37	0.78	1.23
3	Киснемского	0.9	2.0	0.65	1.41

Построим графики.

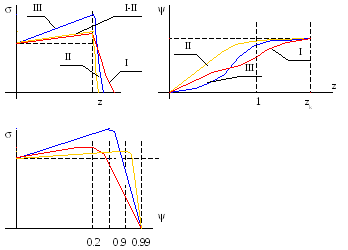
Из таблицы и графиков следует что: зерно Киснемского имеет наибольшую прогрессивность ( _s=2) и наименьшую , т.е. оголеннее.

7-ми канальный порох имеет более ранний распад и большую толщину продуктов распада.

Характеристики , , , для прогрессивной формы.

I фаза. Методика как для ленты. Характеристика растянутости по длине =e₁/c=2e₁/2c остается та же. Вместо =e₁/b приняты две характеристики:

1. П ₁ – отношение периметра сечения бруска к периметру окружности, построенной на длине 2с, как на диаметре:

2. Q ₁ – отношение площади поперечного сечения зерна с каналами к площади круга того же диаметра 2с:

Б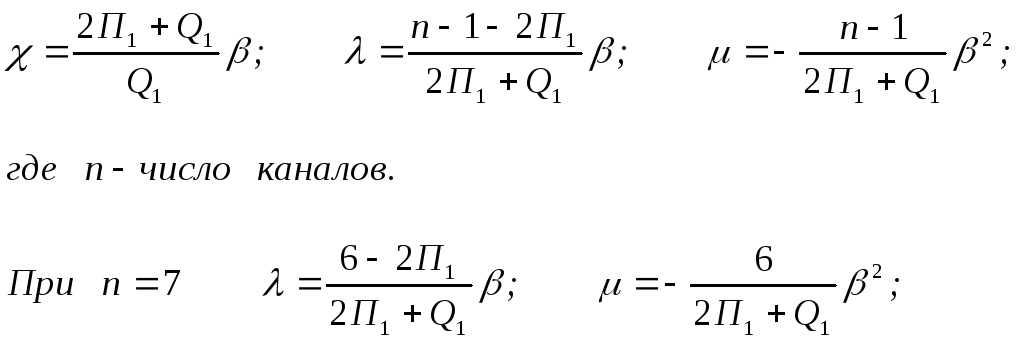 ез вывода запишем:

Эти формулы можно применять для любых форм порохов, они являются общими.

I I фаза. Точная зависимость получена Оппоковым, но пользуются приближенной (по линейному закону), зависимость следовательно будет 2^х – членная. Перенесем начало координат (z_s=1;=_s) будем иметь -_s=₂(z-1)[1+₂(z-1)], причем 1  z  z_k. Дифференцируем по z 

Для определения ₂ c ₂ необходимы 2 условия: 1) z=z_k; _k=1; 2) z=z_k; =0;

Т огда 1-_s=₂(z_k-1)[1+₂(z_k-1)]; 1+2₂(z_k-1)=0;

Решив получим:

Стандартное зерно 7-ми канальное: z_k=1.532; _s=0.85; ₁=0.72; ₁=0.187; ₂=0.564; ₂=–0.94.

Связь между давлением и условиями заряжания при сгорании пороха в постоянном объеме.

З ависимость для наибольшего давления. Формула Нобля-Абеля.

P_m=/(1-), если =/W₀ получим:

Из уравнения следует, что зависимость p() имеет вид:

Формулу можно преобразовать P_m/-P_m= или P_m/=+P_m. Этой зависимостью пользуются для определения  и  при сжигании в манометрической бомбе. Зная P_m1 и P_m2 при соответствующих ₁ и ₂ :

P_m1/₁=+P_m1; P_m2/₂=+P_m2.

В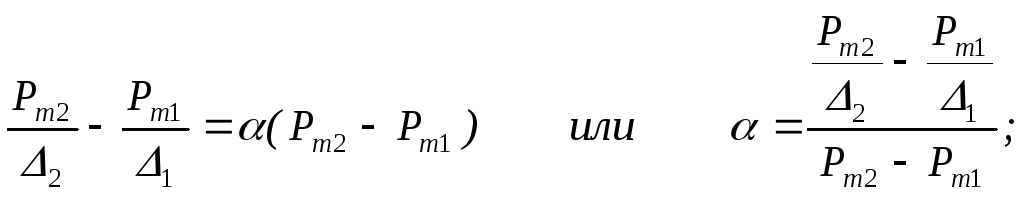 ычитая одно из другого получим:

А затем из выражения находим  (обычно ₁=0.1;  ₂=0.20.25).

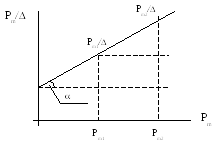
Зависимость p() – основная зависимость.



 удельный объем пороховых газов.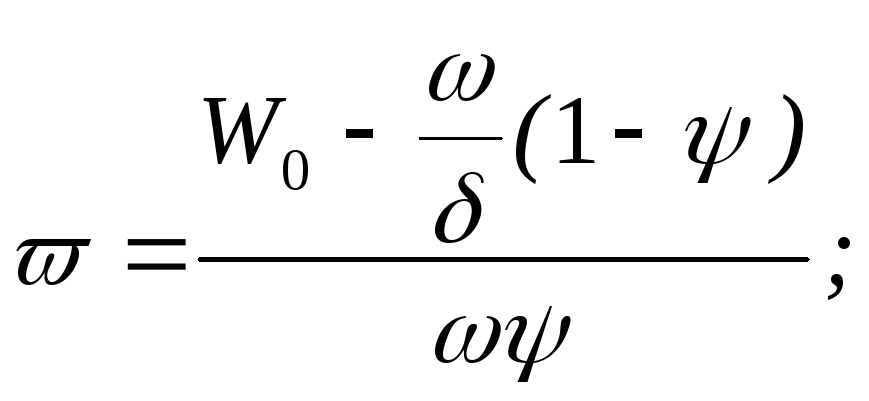

- масса пороха. _r – текущая масса газа; =_r/ - отн. часть; _r=; (1-) – масса несгоревшего пороха. Из уравнения состояния P(-)=RT;

З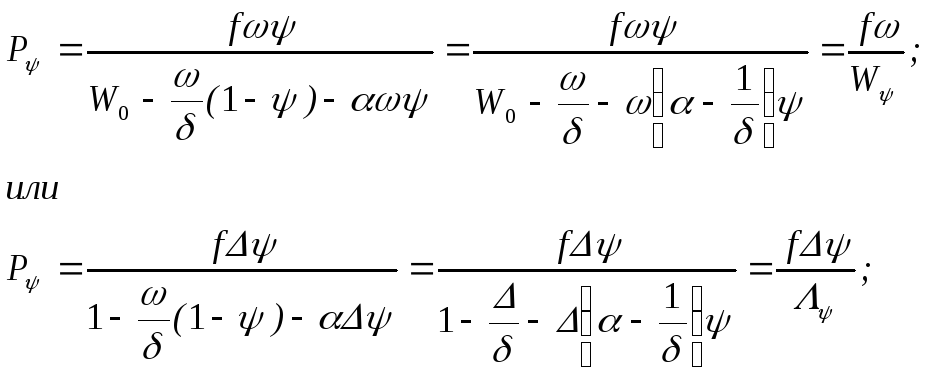 аменим RT₁= и получим:

Здесь W_=W₀-(/)(1-)- - свободный объем.

По мере сгорания пороха W_; 0   1

W₀-/(1-)->W₀-;

Обозначим W₀-/=W_; W₀-=W₁;

W₀>W_>W₁; W₁/W_=(W₀-)/(W₀-/)=(1-)/1-/)<1.

Учет влияния воспламенителя на давление в замкнутом объеме.

Пусть известны характеристики:

_в, _в, _в – для воспламенителя.

, , ,  - для основного заряда.

И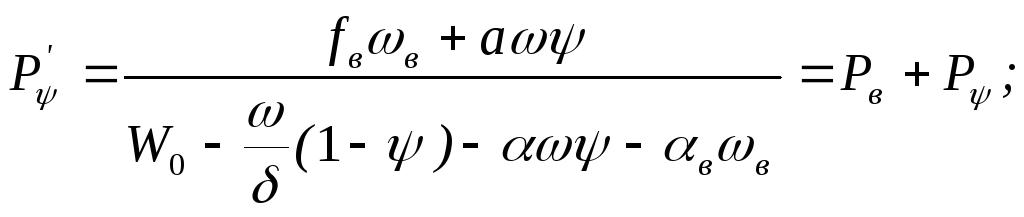 спользуя принцип порциального давления получим:

(P_’= P_в +P_);

здесь P_в=_в_в/W_ –давление газов воспламенителя.

P_=/W_ - давление газов заряда без учета давления газов воспламенителя.

_в_в0 ввиду малости.

Т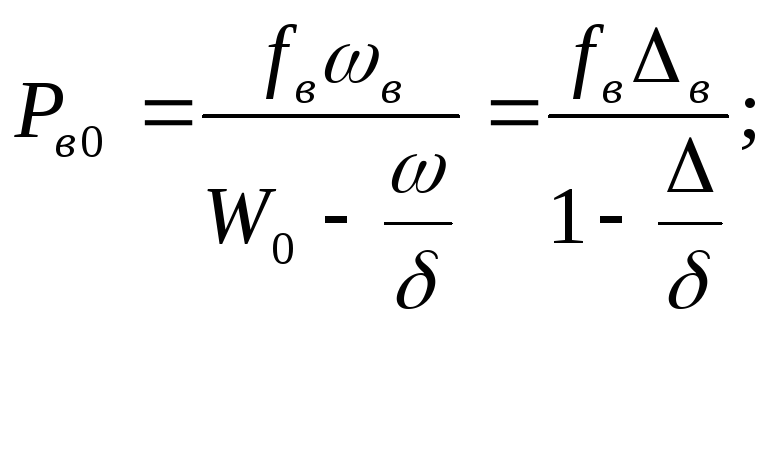 .к. W_ то P_в, однако это не учитывают и рассчитывают P_в0 для начала горения пороха:

Т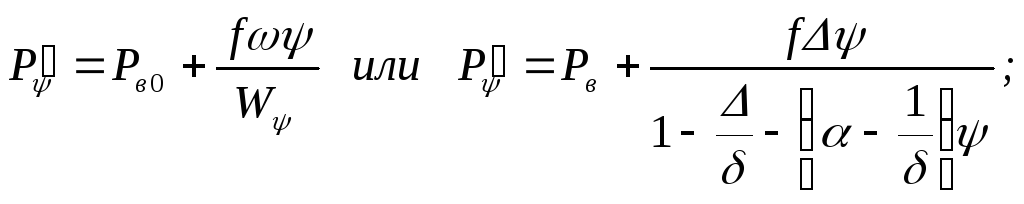 огда зависимость:

П ри сжигании пороха в бомбе известны все характеристики пороха и величина давления, отсюда можно получить (P):

Определение времени горения пороха в постоянном объеме.

И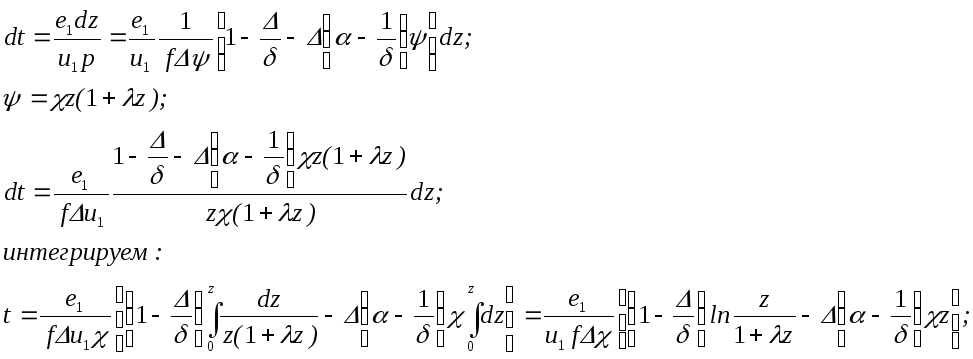 звестно, что u=de/dt откуда dt=de/u; u=u₁p;de=e₁dz;

Зависимость давления от времени.

P =P_в+()/W_ ;=0: W_=W₀-/; =1: W_=W₀-;W_{с р}=1/2;

20